Question and Answers Forum

All Questions Topic List

OthersQuestion and Answers: Page 18

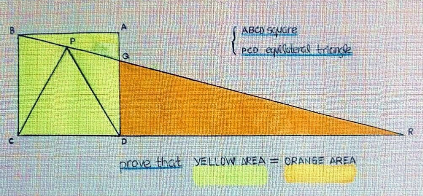
Question Number 185847 Answers: 0 Comments: 0

Question Number 185786 Answers: 0 Comments: 0

Question Number 185781 Answers: 1 Comments: 0

Question Number 185553 Answers: 1 Comments: 0

Question Number 185518 Answers: 0 Comments: 1

Find the radius of convergence of Σ_(n=1) ^∞ ne^(−n^2 ) M.m

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{convergence}\:\mathrm{of} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{ne}^{−\mathrm{n}^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 185517 Answers: 1 Comments: 0

Question Number 185470 Answers: 0 Comments: 3

Determine whether the series U_n =((1+2n^2 )/(1+n^2 )) is convergent or not M.m

$$\mathrm{Determine}\:\mathrm{whether}\:\mathrm{the}\:\mathrm{series} \\ $$$$\mathrm{U}_{\mathrm{n}} =\frac{\mathrm{1}+\mathrm{2n}^{\mathrm{2}} }{\mathrm{1}+\mathrm{n}^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{convergent}\:\mathrm{or}\:\mathrm{not} \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 185450 Answers: 0 Comments: 1

Write down the expansion of (a) cosx (b) (1/(l+x)), and hence show that ((cosx)/(1+x)) = 1−x+(x^2 /2)−(x^3 /2)+((13x^4 )/(24))+... M.m

$$\mathrm{Write}\:\mathrm{down}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\: \\ $$$$\left(\mathrm{a}\right)\:\mathrm{cosx}\:\left(\mathrm{b}\right)\:\frac{\mathrm{1}}{\mathrm{l}+\mathrm{x}},\:\mathrm{and}\:\mathrm{hence}\:\mathrm{show} \\ $$$$\mathrm{that}\:\frac{\mathrm{cosx}}{\mathrm{1}+\mathrm{x}}\:=\:\mathrm{1}−\mathrm{x}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}+\frac{\mathrm{13x}^{\mathrm{4}} }{\mathrm{24}}+... \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 185449 Answers: 1 Comments: 0

Find the first four terms in the expansion of ((x−3)/((1−x^2 )^2 (2+x^2 ))) in ascending power of x. M.m

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{first}\:\mathrm{four}\:\mathrm{terms}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{expansion}\:\mathrm{of}\:\frac{\mathrm{x}−\mathrm{3}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{2}+\mathrm{x}^{\mathrm{2}} \right)}\:\mathrm{in} \\ $$$$\mathrm{ascending}\:\mathrm{power}\:\mathrm{of}\:\mathrm{x}. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 185401 Answers: 0 Comments: 1

Show that ((1+z)/(1−z)) + ((1+z^ )/(1−z^ )) = ((2(1−∣z∣^2 ))/(∣1−z∣^2 )) Where z is a complex number Help!

$$\mathrm{Show}\:\mathrm{that}\:\frac{\mathrm{1}+\mathrm{z}}{\mathrm{1}−\mathrm{z}}\:+\:\frac{\mathrm{1}+\bar {\mathrm{z}}}{\mathrm{1}−\bar {\mathrm{z}}}\:=\:\frac{\mathrm{2}\left(\mathrm{1}−\mid\mathrm{z}\mid^{\mathrm{2}} \right)}{\mid\mathrm{1}−\mathrm{z}\mid^{\mathrm{2}} } \\ $$$$\mathrm{Where}\:\mathrm{z}\:\mathrm{is}\:\mathrm{a}\:\mathrm{complex}\:\mathrm{number} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Question Number 185374 Answers: 1 Comments: 0

lim_(z→∞) ((iz^3 +iz−1)/((2z+3i)(z−i)^2 )) M.m

$$\mathrm{li}\underset{\mathrm{z}\rightarrow\infty} {\mathrm{m}}\frac{\mathrm{iz}^{\mathrm{3}} +\mathrm{iz}−\mathrm{1}}{\left(\mathrm{2z}+\mathrm{3i}\right)\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 185371 Answers: 1 Comments: 0

(1−z)(1−z^− ) = ? Where z is the complex number .

$$\left(\mathrm{1}−\mathrm{z}\right)\left(\mathrm{1}−\overset{−} {\mathrm{z}}\right)\:=\:? \\ $$$$\mathrm{Where}\:\mathrm{z}\:\mathrm{is}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{number} \\ $$$$ \\ $$$$. \\ $$

Question Number 185278 Answers: 1 Comments: 3

Show that f(z)=z^2 is harmonic in polar form

$$\mathrm{Show}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{z}\right)=\mathrm{z}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{harmonic}\:\mathrm{in} \\ $$$$\mathrm{polar}\:\mathrm{form} \\ $$

Question Number 185245 Answers: 1 Comments: 1

Show that f(z)=z^2 is uniformly continous in the region ∣z∣<R where 0<R<∞. Help!

$$\mathrm{Show}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{z}\right)=\mathrm{z}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{uniformly} \\ $$$$\mathrm{continous}\:\mathrm{in}\:\mathrm{the}\:\mathrm{region}\:\mid\mathrm{z}\mid<\mathrm{R} \\ $$$$\mathrm{where}\:\mathrm{0}<\mathrm{R}<\infty. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Question Number 185243 Answers: 1 Comments: 3

Using ε−δ approach prove that lim_(z→i) ((3z^4 −2z^3 +8z^2 −2z+5)/(z−i))=4+4i Help!

$$\mathrm{Using}\:\varepsilon−\delta\:\mathrm{approach}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\mathrm{li}\underset{\mathrm{z}\rightarrow\mathrm{i}} {\mathrm{m}}\frac{\mathrm{3z}^{\mathrm{4}} −\mathrm{2z}^{\mathrm{3}} +\mathrm{8z}^{\mathrm{2}} −\mathrm{2z}+\mathrm{5}}{\mathrm{z}−\mathrm{i}}=\mathrm{4}+\mathrm{4i} \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Question Number 185181 Answers: 2 Comments: 3

Question Number 185038 Answers: 1 Comments: 0

Find the range of values of x for which the series (x/(27))+(x^2 /(125))+...+(x^n /((2n+1)^3 ))+... is absolutely convergent. Help!

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{values}\:\mathrm{of}\:\mathrm{x}\:\mathrm{for}\:\mathrm{which} \\ $$$$\mathrm{the}\:\mathrm{series}\:\frac{\mathrm{x}}{\mathrm{27}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{125}}+...+\frac{\mathrm{x}^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{3}} }+... \\ $$$$\mathrm{is}\:\mathrm{absolutely}\:\mathrm{convergent}. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Question Number 185036 Answers: 1 Comments: 0

Find the series for cosx. Hence, deduce series sin^2 x and show that, if x is small, ((sin^2 x−x^2 cosx)/x^4 )=(1/6)+(x^2 /(360)) approximately. Help!

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{series}\:\mathrm{for}\:\mathrm{cosx}.\:\mathrm{Hence},\: \\ $$$$\mathrm{deduce}\:\mathrm{series}\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{and}\:\mathrm{show}\:\mathrm{that}, \\ $$$$\mathrm{if}\:\mathrm{x}\:\mathrm{is}\:\mathrm{small},\:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{x}^{\mathrm{2}} \mathrm{cosx}}{\mathrm{x}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{360}} \\ $$$$\mathrm{approximately}. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$

Question Number 185014 Answers: 1 Comments: 1

The relation y=x^2 +kx+c, where K and C are constant passes through the points (−1, −2) and (1, 8) in the coordinate axes. calculate the value of C and K. M.m

$$\mathrm{The}\:\mathrm{relation}\:\mathrm{y}=\mathrm{x}^{\mathrm{2}} +\mathrm{kx}+\mathrm{c},\:\mathrm{where}\:\mathrm{K} \\ $$$$\mathrm{and}\:\mathrm{C}\:\mathrm{are}\:\mathrm{constant}\:\mathrm{passes}\:\mathrm{through} \\ $$$$\mathrm{the}\:\mathrm{points}\:\left(−\mathrm{1},\:−\mathrm{2}\right)\:\mathrm{and}\:\left(\mathrm{1},\:\mathrm{8}\right)\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{coordinate}\:\mathrm{axes}.\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{of}\:\mathrm{C}\:\mathrm{and}\:\mathrm{K}. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{M}.\mathrm{m} \\ $$

Question Number 185116 Answers: 1 Comments: 0