Question and Answers Forum

OthersQuestion and Answers: Page 131

Question Number 23823 Answers: 1 Comments: 0

The period of a simple pendulum A is 6 secs. Find the period of a simple pendulum B, if A makes 30 oscillation in the time it takes B to make 70 oscillation.

$$\mathrm{The}\:\mathrm{period}\:\mathrm{of}\:\mathrm{a}\:\mathrm{simple}\:\mathrm{pendulum}\:\mathrm{A}\:\mathrm{is}\:\mathrm{6}\:\mathrm{secs}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{period}\:\mathrm{of}\:\mathrm{a}\:\mathrm{simple} \\ $$$$\mathrm{pendulum}\:\mathrm{B},\:\mathrm{if}\:\mathrm{A}\:\mathrm{makes}\:\mathrm{30}\:\mathrm{oscillation}\:\mathrm{in}\:\mathrm{the}\:\mathrm{time}\:\mathrm{it}\:\mathrm{takes}\:\mathrm{B}\:\mathrm{to}\:\mathrm{make}\:\mathrm{70} \\ $$$$\mathrm{oscillation}. \\ $$

Question Number 23773 Answers: 0 Comments: 2

I have a leaderboard with the data of ′runners′. Each runner has a ′place′ (1st, 2nd, etc.), and a ′time′ (in seconds). Every day I have been comparing the data. What information is important to note when looking at data such as this? Is it possible to make predictions of future data? I′d love advice for things I can do with monitoring these kinds of statistics!

$$\mathrm{I}\:\mathrm{have}\:\mathrm{a}\:\mathrm{leaderboard}\:\mathrm{with}\:\mathrm{the}\:\mathrm{data}\:\mathrm{of}\:'\mathrm{runners}'. \\ $$$$\mathrm{Each}\:\mathrm{runner}\:\mathrm{has}\:\mathrm{a}\:'\mathrm{place}'\:\left(\mathrm{1st},\:\mathrm{2nd},\:\mathrm{etc}.\right), \\ $$$$\mathrm{and}\:\mathrm{a}\:'\mathrm{time}'\:\left(\mathrm{in}\:\mathrm{seconds}\right). \\ $$$$\: \\ $$$$\mathrm{Every}\:\mathrm{day}\:\mathrm{I}\:\mathrm{have}\:\mathrm{been}\:\mathrm{comparing}\:\mathrm{the}\:\mathrm{data}. \\ $$$$\mathrm{What}\:\mathrm{information}\:\mathrm{is}\:\mathrm{important}\:\mathrm{to}\:\mathrm{note}\:\mathrm{when} \\ $$$$\mathrm{looking}\:\mathrm{at}\:\mathrm{data}\:\mathrm{such}\:\mathrm{as}\:\mathrm{this}? \\ $$$$\: \\ $$$$\mathrm{Is}\:\mathrm{it}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{make}\:\mathrm{predictions}\:\mathrm{of}\:\mathrm{future}\:\mathrm{data}? \\ $$$$\: \\ $$$$\mathrm{I}'\mathrm{d}\:\mathrm{love}\:\mathrm{advice}\:\mathrm{for}\:\mathrm{things}\:\mathrm{I}\:\mathrm{can}\:\mathrm{do}\:\mathrm{with}\:\mathrm{monitoring} \\ $$$$\mathrm{these}\:\mathrm{kinds}\:\mathrm{of}\:\mathrm{statistics}! \\ $$

Question Number 23715 Answers: 0 Comments: 0

Why ΔS > 0 for the reaction 2HgO(s) → 2Hg(l) + O_2 (g)?

$$\mathrm{Why}\:\Delta\mathrm{S}\:>\:\mathrm{0}\:\mathrm{for}\:\mathrm{the}\:\mathrm{reaction} \\ $$$$\mathrm{2HgO}\left(\mathrm{s}\right)\:\rightarrow\:\mathrm{2Hg}\left({l}\right)\:+\:\mathrm{O}_{\mathrm{2}} \left(\mathrm{g}\right)? \\ $$

Question Number 23711 Answers: 1 Comments: 0

A certain ideal gas has C_(v, m) = a + bT, where a = 25 J/(mol. K) and b = 0.03 J(mol.K^2 ). Let 2 mole of this gas go from 300 K and 2 litre volume to 600 K and 4 litre. ΔS_(gas) is

$$\mathrm{A}\:\mathrm{certain}\:\mathrm{ideal}\:\mathrm{gas}\:\mathrm{has}\:\mathrm{C}_{\mathrm{v},\:\mathrm{m}} \:=\:\mathrm{a}\:+\:\mathrm{bT}, \\ $$$$\mathrm{where}\:\mathrm{a}\:=\:\mathrm{25}\:\mathrm{J}/\left(\mathrm{mol}.\:\mathrm{K}\right)\:\mathrm{and}\:\mathrm{b}\:=\:\mathrm{0}.\mathrm{03} \\ $$$$\mathrm{J}\left(\mathrm{mol}.\mathrm{K}^{\mathrm{2}} \right).\:\mathrm{Let}\:\mathrm{2}\:\mathrm{mole}\:\mathrm{of}\:\mathrm{this}\:\mathrm{gas}\:\mathrm{go} \\ $$$$\mathrm{from}\:\mathrm{300}\:\mathrm{K}\:\mathrm{and}\:\mathrm{2}\:\mathrm{litre}\:\mathrm{volume}\:\mathrm{to}\:\mathrm{600}\:\mathrm{K} \\ $$$$\mathrm{and}\:\mathrm{4}\:\mathrm{litre}.\:\Delta\mathrm{S}_{\mathrm{gas}} \:\mathrm{is} \\ $$

Question Number 23707 Answers: 1 Comments: 4

Two blocks A and B of mass 1 kg and 2 kg respectively are connected by a string, passing over a light frictionless pulley. Both the blocks are resting on a horizontal floor and the pulley is held such that string remains just taut. At time t = 0, a force F = 20t N, starts acting on the pulley along vertically upward direction. Calculate vertical displacement of the pulley upto the instant when B loses contact with the floor.

$$\mathrm{Two}\:\mathrm{blocks}\:{A}\:\mathrm{and}\:{B}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{1}\:\mathrm{kg}\:\mathrm{and} \\ $$$$\mathrm{2}\:\mathrm{kg}\:\mathrm{respectively}\:\mathrm{are}\:\mathrm{connected}\:\mathrm{by}\:\mathrm{a} \\ $$$$\mathrm{string},\:\mathrm{passing}\:\mathrm{over}\:\mathrm{a}\:\mathrm{light}\:\mathrm{frictionless} \\ $$$$\mathrm{pulley}.\:\mathrm{Both}\:\mathrm{the}\:\mathrm{blocks}\:\mathrm{are}\:\mathrm{resting}\:\mathrm{on}\:\mathrm{a} \\ $$$$\mathrm{horizontal}\:\mathrm{floor}\:\mathrm{and}\:\mathrm{the}\:\mathrm{pulley}\:\mathrm{is}\:\mathrm{held} \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{string}\:\mathrm{remains}\:\mathrm{just}\:\mathrm{taut}.\:\mathrm{At} \\ $$$$\mathrm{time}\:{t}\:=\:\mathrm{0},\:\mathrm{a}\:\mathrm{force}\:{F}\:=\:\mathrm{20}{t}\:\mathrm{N},\:\mathrm{starts} \\ $$$$\mathrm{acting}\:\mathrm{on}\:\mathrm{the}\:\mathrm{pulley}\:\mathrm{along}\:\mathrm{vertically} \\ $$$$\mathrm{upward}\:\mathrm{direction}.\:\mathrm{Calculate}\:\mathrm{vertical} \\ $$$$\mathrm{displacement}\:\mathrm{of}\:\mathrm{the}\:\mathrm{pulley}\:\mathrm{upto}\:\mathrm{the} \\ $$$$\mathrm{instant}\:\mathrm{when}\:{B}\:\mathrm{loses}\:\mathrm{contact}\:\mathrm{with}\:\mathrm{the} \\ $$$$\mathrm{floor}. \\ $$

Question Number 24506 Answers: 0 Comments: 8

A spot light S rotates in a horizontal plane with a constant angular velocity of 0.1 rad/s. The spot of light P moves along the wall at a distance 3 m. What is the velocity of the spot P when θ = 45°?

$$\mathrm{A}\:\mathrm{spot}\:\mathrm{light}\:{S}\:\mathrm{rotates}\:\mathrm{in}\:\mathrm{a}\:\mathrm{horizontal} \\ $$$$\mathrm{plane}\:\mathrm{with}\:\mathrm{a}\:\mathrm{constant}\:\mathrm{angular}\:\mathrm{velocity} \\ $$$$\mathrm{of}\:\mathrm{0}.\mathrm{1}\:\mathrm{rad}/\mathrm{s}.\:\mathrm{The}\:\mathrm{spot}\:\mathrm{of}\:\mathrm{light}\:{P}\:\mathrm{moves} \\ $$$$\mathrm{along}\:\mathrm{the}\:\mathrm{wall}\:\mathrm{at}\:\mathrm{a}\:\mathrm{distance}\:\mathrm{3}\:\mathrm{m}.\:\mathrm{What} \\ $$$$\mathrm{is}\:\mathrm{the}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{the}\:\mathrm{spot}\:{P}\:\mathrm{when}\:\theta\:=\:\mathrm{45}°? \\ $$

Question Number 23694 Answers: 0 Comments: 0

Calculate the lattice enthalpy of MgBr_2 . Given that Enthalpy of formation of MgBr_2 = −524 kJ mol^(−1) Sublimation energy of Mg = +2187 kJ mol^(−1) Vaporisation energy of Br_2 (l) = +31 kJ mol^(−1) Dissociation energy of Br_2 (g) = +193 kJ mol^(−1) Electron gain enthalpy of Br = −331 kJ mol^(−1)

$${Calculate}\:{the}\:{lattice}\:{enthalpy}\:{of}\:{MgBr}_{\mathrm{2}} . \\ $$$${Given}\:{that} \\ $$$${Enthalpy}\:{of}\:{formation}\:{of}\:{MgBr}_{\mathrm{2}} \:=\:−\mathrm{524} \\ $$$${kJ}\:{mol}^{−\mathrm{1}} \\ $$$${Sublimation}\:{energy}\:{of}\:{Mg}\:=\:+\mathrm{2187} \\ $$$${kJ}\:{mol}^{−\mathrm{1}} \\ $$$${Vaporisation}\:{energy}\:{of}\:{Br}_{\mathrm{2}} \left({l}\right)\:=\:+\mathrm{31} \\ $$$${kJ}\:{mol}^{−\mathrm{1}} \\ $$$${Dissociation}\:{energy}\:{of}\:{Br}_{\mathrm{2}} \left({g}\right)\:=\:+\mathrm{193} \\ $$$${kJ}\:{mol}^{−\mathrm{1}} \\ $$$${Electron}\:{gain}\:{enthalpy}\:{of}\:{Br}\:=\:−\mathrm{331} \\ $$$${kJ}\:{mol}^{−\mathrm{1}} \\ $$

Question Number 23739 Answers: 0 Comments: 3

Question Number 23666 Answers: 2 Comments: 1

A uniform rope of length L and mass per unit λ having one end fixed with the ceiling is released from rest. Find the tension in the fixed end as a function of the distance travelled by the movable end.

$$\mathrm{A}\:\mathrm{uniform}\:\mathrm{rope}\:\mathrm{of}\:\mathrm{length}\:{L}\:\mathrm{and}\:\mathrm{mass} \\ $$$$\mathrm{per}\:\mathrm{unit}\:\lambda\:\mathrm{having}\:\mathrm{one}\:\mathrm{end}\:\mathrm{fixed}\:\mathrm{with} \\ $$$$\mathrm{the}\:\mathrm{ceiling}\:\mathrm{is}\:\mathrm{released}\:\mathrm{from}\:\mathrm{rest}.\:\mathrm{Find} \\ $$$$\mathrm{the}\:\mathrm{tension}\:\mathrm{in}\:\mathrm{the}\:\mathrm{fixed}\:\mathrm{end}\:\mathrm{as}\:\mathrm{a}\:\mathrm{function} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{travelled}\:\mathrm{by}\:\mathrm{the}\:\mathrm{movable} \\ $$$$\mathrm{end}. \\ $$

Question Number 23645 Answers: 0 Comments: 1

Ethylene on combustion gives carbon dioxide and water. Its enthalpy of combustion is 1410 kJ/mol. If the enthalpy of formation of CO_2 and H_2 O are 393.3 kJ and 286.2 kJ respectively. Calculate the enthalpy of formation of ethylene.

$$\mathrm{Ethylene}\:\mathrm{on}\:\mathrm{combustion}\:\mathrm{gives}\:\mathrm{carbon} \\ $$$$\mathrm{dioxide}\:\mathrm{and}\:\mathrm{water}.\:\mathrm{Its}\:\mathrm{enthalpy}\:\mathrm{of} \\ $$$$\mathrm{combustion}\:\mathrm{is}\:\mathrm{1410}\:\mathrm{kJ}/\mathrm{mol}.\:\mathrm{If}\:\mathrm{the} \\ $$$$\mathrm{enthalpy}\:\mathrm{of}\:\mathrm{formation}\:\mathrm{of}\:\mathrm{CO}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{H}_{\mathrm{2}} \mathrm{O} \\ $$$$\mathrm{are}\:\mathrm{393}.\mathrm{3}\:\mathrm{kJ}\:\mathrm{and}\:\mathrm{286}.\mathrm{2}\:\mathrm{kJ}\:\mathrm{respectively}. \\ $$$$\mathrm{Calculate}\:\mathrm{the}\:\mathrm{enthalpy}\:\mathrm{of}\:\mathrm{formation}\:\mathrm{of} \\ $$$$\mathrm{ethylene}. \\ $$

Question Number 23632 Answers: 0 Comments: 9

Question Number 23617 Answers: 2 Comments: 3

The system is released from rest. All surfaces are smooth. Find the angle θ at which the acceleration of wedge is maximum. (given (M/m) = (1/2))

$$\mathrm{The}\:\mathrm{system}\:\mathrm{is}\:\mathrm{released}\:\mathrm{from}\:\mathrm{rest}.\:\mathrm{All} \\ $$$$\mathrm{surfaces}\:\mathrm{are}\:\mathrm{smooth}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{angle}\:\theta\:\mathrm{at} \\ $$$$\mathrm{which}\:\mathrm{the}\:\mathrm{acceleration}\:\mathrm{of}\:\mathrm{wedge}\:\mathrm{is} \\ $$$$\mathrm{maximum}.\:\left(\mathrm{given}\:\frac{{M}}{{m}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$

Question Number 23559 Answers: 1 Comments: 1

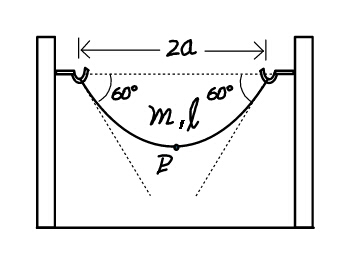
Question Number 23556 Answers: 1 Comments: 0

A ball falls vertically on to a floor, with momentum p, and then bounces repeatedly, the coefficient of restitution is e. The total momentum imparted by the ball to the floor is

$$\mathrm{A}\:\mathrm{ball}\:\mathrm{falls}\:\mathrm{vertically}\:\mathrm{on}\:\mathrm{to}\:\mathrm{a}\:\mathrm{floor},\:\mathrm{with} \\ $$$$\mathrm{momentum}\:{p},\:\mathrm{and}\:\mathrm{then}\:\mathrm{bounces} \\ $$$$\mathrm{repeatedly},\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{restitution} \\ $$$$\mathrm{is}\:{e}.\:\mathrm{The}\:\mathrm{total}\:\mathrm{momentum}\:\mathrm{imparted}\:\mathrm{by} \\ $$$$\mathrm{the}\:\mathrm{ball}\:\mathrm{to}\:\mathrm{the}\:\mathrm{floor}\:\mathrm{is} \\ $$

Question Number 23548 Answers: 0 Comments: 3

Question Number 23585 Answers: 0 Comments: 0

No work is done by a force on an object if (1) the object is stationary but the point of application of the force moves on the object (2) the object moves in such a way that the point of application of the force remains fixed (3) the force is always perpendicular to its velocity (4) the force is always perpendicular to its acceleration.

$$\mathrm{No}\:\mathrm{work}\:\mathrm{is}\:\mathrm{done}\:\mathrm{by}\:\mathrm{a}\:\mathrm{force}\:\mathrm{on}\:\mathrm{an}\:\mathrm{object}\:\mathrm{if} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{the}\:\mathrm{object}\:\mathrm{is}\:\mathrm{stationary}\:\mathrm{but}\:\mathrm{the} \\ $$$$\mathrm{point}\:\mathrm{of}\:\mathrm{application}\:\mathrm{of}\:\mathrm{the}\:\mathrm{force}\:\mathrm{moves} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{object} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{the}\:\mathrm{object}\:\mathrm{moves}\:\mathrm{in}\:\mathrm{such}\:\mathrm{a}\:\mathrm{way} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{point}\:\mathrm{of}\:\mathrm{application}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{force}\:\mathrm{remains}\:\mathrm{fixed} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{the}\:\mathrm{force}\:\mathrm{is}\:\mathrm{always}\:\mathrm{perpendicular}\:\mathrm{to} \\ $$$$\mathrm{its}\:\mathrm{velocity} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{the}\:\mathrm{force}\:\mathrm{is}\:\mathrm{always}\:\mathrm{perpendicular}\:\mathrm{to} \\ $$$$\mathrm{its}\:\mathrm{acceleration}. \\ $$

Question Number 23531 Answers: 1 Comments: 3

Question Number 23520 Answers: 0 Comments: 3

A wooden block of mass 10 gm is dropped from the top of a tower 100 m high. Simultaneously, a bullet of mass 10 gm is fired from the foot of the tower vertically upwards with a velocity of 100 m/sec. If the bullet is embedded in it, how high will it rise above the tower before it starts falling? (Consider g = 10 m/sec^2 )

$$\mathrm{A}\:\mathrm{wooden}\:\mathrm{block}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{10}\:\mathrm{gm}\:\mathrm{is} \\ $$$$\mathrm{dropped}\:\mathrm{from}\:\mathrm{the}\:\mathrm{top}\:\mathrm{of}\:\mathrm{a}\:\mathrm{tower}\:\mathrm{100}\:\mathrm{m} \\ $$$$\mathrm{high}.\:\mathrm{Simultaneously},\:\mathrm{a}\:\mathrm{bullet}\:\mathrm{of}\:\mathrm{mass} \\ $$$$\mathrm{10}\:\mathrm{gm}\:\mathrm{is}\:\mathrm{fired}\:\mathrm{from}\:\mathrm{the}\:\mathrm{foot}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tower} \\ $$$$\mathrm{vertically}\:\mathrm{upwards}\:\mathrm{with}\:\mathrm{a}\:\mathrm{velocity}\:\mathrm{of} \\ $$$$\mathrm{100}\:\mathrm{m}/\mathrm{sec}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{bullet}\:\mathrm{is}\:\mathrm{embedded}\:\mathrm{in} \\ $$$$\mathrm{it},\:\mathrm{how}\:\mathrm{high}\:\mathrm{will}\:\mathrm{it}\:\mathrm{rise}\:\mathrm{above}\:\mathrm{the}\:\mathrm{tower} \\ $$$$\mathrm{before}\:\mathrm{it}\:\mathrm{starts}\:\mathrm{falling}?\:\left(\mathrm{Consider}\:{g}\:=\right. \\ $$$$\left.\mathrm{10}\:\mathrm{m}/\mathrm{sec}^{\mathrm{2}} \right) \\ $$

Question Number 23492 Answers: 0 Comments: 5

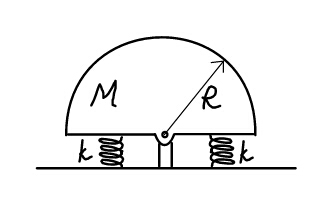
Question Number 23489 Answers: 1 Comments: 2

A rectangular wire frame ABCD is in vertical plane is moving with a constant acceleration a into the plane. Direction of gravity is shown in figure. A collar can move on wire AC of length l. Coefficient of friction between wire and collar is μ. Find (i) The minimum acceleration a so that collar does not slip on wire. (ii) The time taken by collar to reach C if acceleration is half the value calculated in part (i)

$$\mathrm{A}\:\mathrm{rectangular}\:\mathrm{wire}\:\mathrm{frame}\:{ABCD}\:\mathrm{is}\:\mathrm{in} \\ $$$$\mathrm{vertical}\:\mathrm{plane}\:\mathrm{is}\:\mathrm{moving}\:\mathrm{with}\:\mathrm{a}\:\mathrm{constant} \\ $$$$\mathrm{acceleration}\:{a}\:\mathrm{into}\:\mathrm{the}\:\mathrm{plane}.\:\mathrm{Direction} \\ $$$$\mathrm{of}\:\mathrm{gravity}\:\mathrm{is}\:\mathrm{shown}\:\mathrm{in}\:\mathrm{figure}.\:\mathrm{A}\:\mathrm{collar} \\ $$$$\mathrm{can}\:\mathrm{move}\:\mathrm{on}\:\mathrm{wire}\:{AC}\:\mathrm{of}\:\mathrm{length}\:{l}. \\ $$$$\mathrm{Coefficient}\:\mathrm{of}\:\mathrm{friction}\:\mathrm{between}\:\mathrm{wire} \\ $$$$\mathrm{and}\:\mathrm{collar}\:\mathrm{is}\:\mu.\:\mathrm{Find} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{The}\:\mathrm{minimum}\:\mathrm{acceleration}\:{a}\:\mathrm{so}\:\mathrm{that} \\ $$$$\mathrm{collar}\:\mathrm{does}\:\mathrm{not}\:\mathrm{slip}\:\mathrm{on}\:\mathrm{wire}. \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{The}\:\mathrm{time}\:\mathrm{taken}\:\mathrm{by}\:\mathrm{collar}\:\mathrm{to}\:\mathrm{reach}\:{C} \\ $$$$\mathrm{if}\:\mathrm{acceleration}\:\mathrm{is}\:\mathrm{half}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{calculated}\:\mathrm{in}\:\mathrm{part}\:\left(\mathrm{i}\right) \\ $$

Question Number 23488 Answers: 0 Comments: 0

area of a(1−cos θ)

$${area}\:{of}\:{a}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$

Question Number 23481 Answers: 0 Comments: 5

Which of the diagrams represents variation of total mechanical energy of a pendulum oscillating in air as function of time?

$$\mathrm{Which}\:\mathrm{of}\:\mathrm{the}\:\mathrm{diagrams}\:\mathrm{represents} \\ $$$$\mathrm{variation}\:\mathrm{of}\:\mathrm{total}\:\mathrm{mechanical}\:\mathrm{energy}\:\mathrm{of} \\ $$$$\mathrm{a}\:\mathrm{pendulum}\:\mathrm{oscillating}\:\mathrm{in}\:\mathrm{air}\:\mathrm{as}\:\mathrm{function} \\ $$$$\mathrm{of}\:\mathrm{time}? \\ $$

Question Number 23476 Answers: 0 Comments: 0

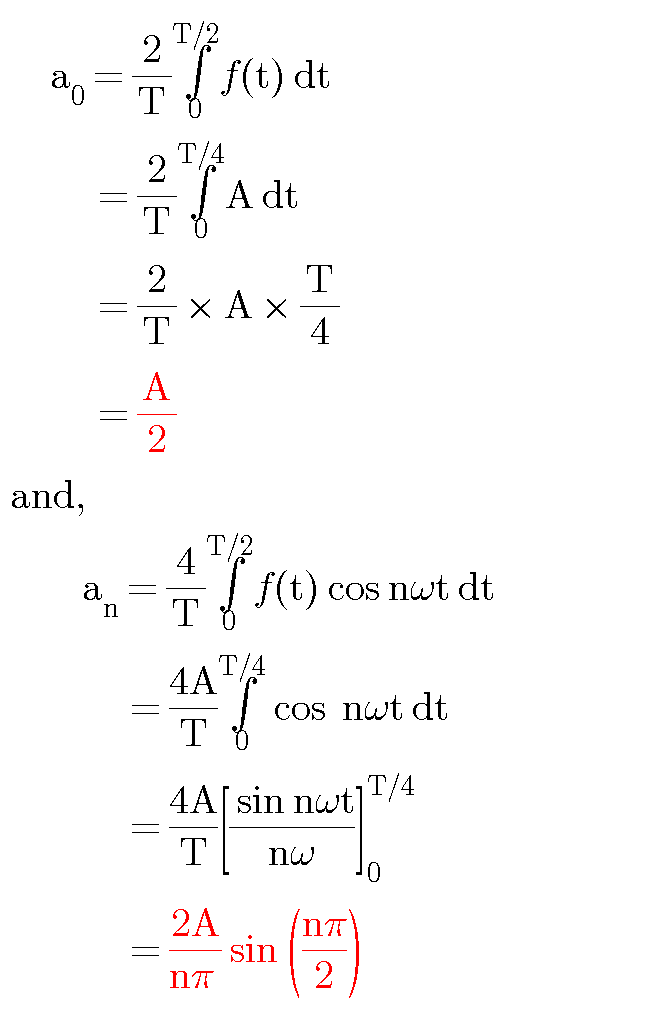
Question Number 23472 Answers: 1 Comments: 1

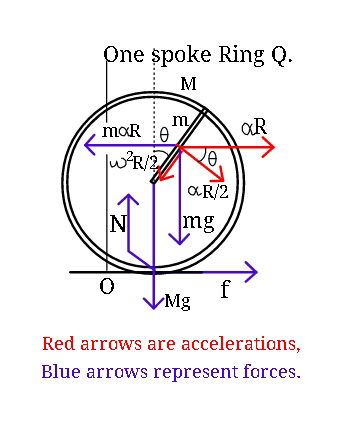
Question Number 23458 Answers: 0 Comments: 1

Question Number 23444 Answers: 0 Comments: 0

Pg 126 Pg 127 Pg 128 Pg 129 Pg 130 Pg 131 Pg 132 Pg 133 Pg 134 Pg 135

Contact: info@tinkutara.com