
OthersQuestion and Answers: Page 124
Question Number 26681 Answers: 0 Comments: 1
Question Number 26634 Answers: 1 Comments: 1

Question Number 26625 Answers: 1 Comments: 0
Question Number 26623 Answers: 2 Comments: 0
Question Number 26581 Answers: 0 Comments: 0

Question Number 26580 Answers: 0 Comments: 0

Question Number 26544 Answers: 1 Comments: 0
$$\int\mathrm{1}/{x}^{\mathrm{2}} +{y}^{\mathrm{2}} {dydx} \\ $$
Question Number 26601 Answers: 1 Comments: 0
Question Number 26528 Answers: 1 Comments: 0
Question Number 26513 Answers: 0 Comments: 2
Question Number 26456 Answers: 0 Comments: 1

Question Number 26455 Answers: 0 Comments: 0

Question Number 26454 Answers: 0 Comments: 0

Question Number 26442 Answers: 0 Comments: 1
Question Number 26425 Answers: 0 Comments: 0
Question Number 26424 Answers: 0 Comments: 0
Question Number 26382 Answers: 0 Comments: 1

Question Number 26381 Answers: 0 Comments: 9

Question Number 26380 Answers: 0 Comments: 0

Question Number 26352 Answers: 1 Comments: 0
Question Number 26329 Answers: 1 Comments: 0
Question Number 26328 Answers: 1 Comments: 1
Question Number 26320 Answers: 2 Comments: 3
$$\mathrm{solve}\:{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{2}^{{x}} \\ $$
Question Number 26312 Answers: 0 Comments: 6
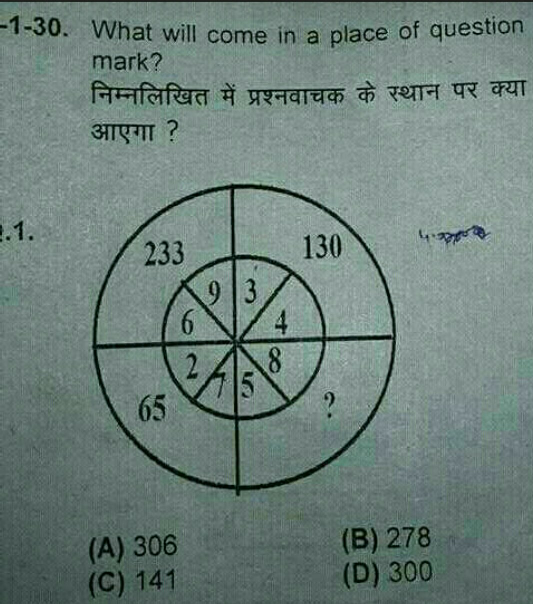
Question Number 26298 Answers: 0 Comments: 2
$${y}=\mathrm{sin}\:^{\mathrm{4}} {x} \\ $$$${y}'=?\:{differential} \\ $$
Question Number 26354 Answers: 1 Comments: 0
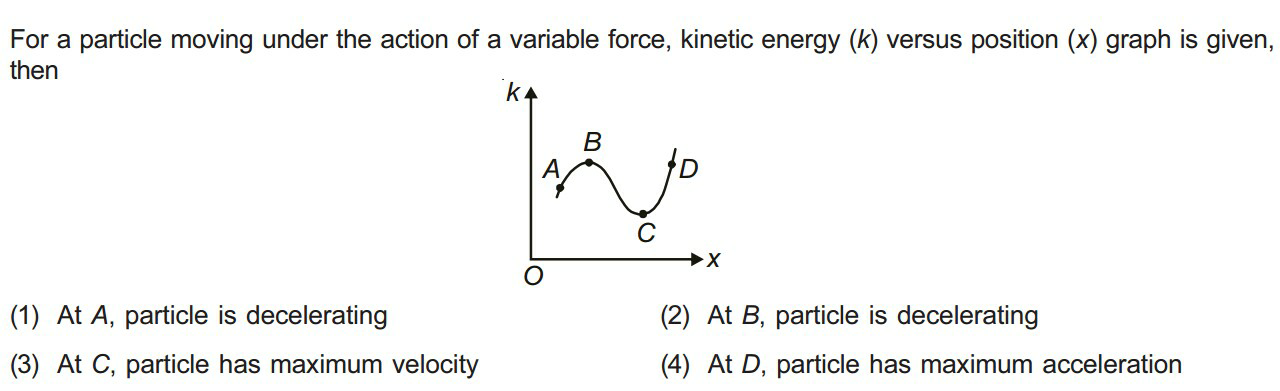
Pg 119 Pg 120 Pg 121 Pg 122 Pg 123 Pg 124 Pg 125 Pg 126 Pg 127 Pg 128
