Question and Answers Forum

OthersQuestion and Answers: Page 101

Question Number 52079 Answers: 1 Comments: 1

Sum to the n terms of the series whose n^(th ) term is 2^(n−1 ) + 8n^3 −6n^2

$${Sum}\:{to}\:{the}\:{n}\:{terms}\:{of}\:{the}\:{series}\:{whose}\:{n}^{{th}\:} \:{term}\:{is}\:\mathrm{2}^{{n}−\mathrm{1}\:} \:+\:\mathrm{8}{n}^{\mathrm{3}} \:−\mathrm{6}{n}^{\mathrm{2}} \\ $$

Question Number 52075 Answers: 0 Comments: 0

Question Number 52025 Answers: 4 Comments: 8

Question Number 51933 Answers: 2 Comments: 1

If p = cos θ + i sin θ and q = cos φ + i sin φ Show that (((p + q)(pq − 1))/((p − q)(pq + 1))) = ((sin θ + sin φ)/(sin θ − sin φ))

$$\mathrm{If}\:\:\mathrm{p}\:=\:\mathrm{cos}\:\theta\:+\:\mathrm{i}\:\mathrm{sin}\:\theta\:\:\:\:\:\:\:\:\:\mathrm{and}\:\:\:\:\:\:\:\:\:\mathrm{q}\:\:=\:\:\mathrm{cos}\:\phi\:+\:\mathrm{i}\:\mathrm{sin}\:\phi \\ $$$$\mathrm{Show}\:\mathrm{that}\:\:\:\:\:\:\:\:\:\frac{\left(\mathrm{p}\:+\:\mathrm{q}\right)\left(\mathrm{pq}\:−\:\mathrm{1}\right)}{\left(\mathrm{p}\:−\:\mathrm{q}\right)\left(\mathrm{pq}\:+\:\mathrm{1}\right)}\:\:=\:\:\frac{\mathrm{sin}\:\theta\:+\:\mathrm{sin}\:\phi}{\mathrm{sin}\:\theta\:−\:\mathrm{sin}\:\phi} \\ $$

Question Number 51897 Answers: 1 Comments: 0

If x + (1/x) = 2cosθ , y + (1/y) = 2cosφ , z + (1/z) = 2cosψ Show that xyz + (1/(xyz)) = 2cos(θ + φ + ψ)

$$\mathrm{If}\:\:\:\:\mathrm{x}\:+\:\frac{\mathrm{1}}{\mathrm{x}}\:\:=\:\:\mathrm{2cos}\theta\:,\:\:\:\:\:\:\mathrm{y}\:+\:\frac{\mathrm{1}}{\mathrm{y}}\:\:=\:\:\mathrm{2cos}\phi\:,\:\:\:\:\:\:\:\:\:\mathrm{z}\:+\:\frac{\mathrm{1}}{\mathrm{z}}\:\:=\:\:\mathrm{2cos}\psi \\ $$$$\mathrm{Show}\:\mathrm{that}\:\:\:\:\:\:\:\:\:\:\mathrm{xyz}\:+\:\frac{\mathrm{1}}{\mathrm{xyz}}\:\:=\:\:\mathrm{2cos}\left(\theta\:+\:\phi\:+\:\psi\right) \\ $$

Question Number 51887 Answers: 1 Comments: 0

Prove that; tanh(log (√3)) = (1/2)

$$\mathrm{Prove}\:\mathrm{that};\:\:\:\:\mathrm{tanh}\left(\mathrm{log}\:\sqrt{\mathrm{3}}\right)\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Question Number 52140 Answers: 2 Comments: 2

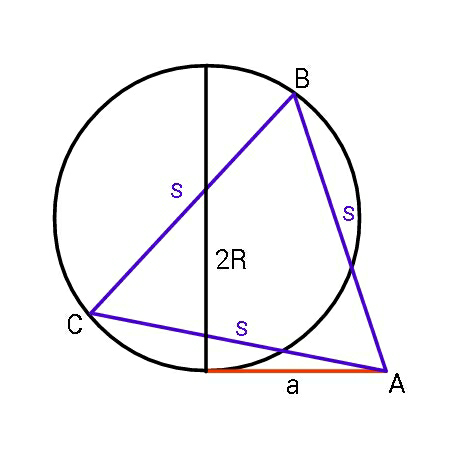
Question Number 51861 Answers: 0 Comments: 1

Question Number 51837 Answers: 1 Comments: 1

Question Number 51721 Answers: 1 Comments: 0

Find the range of value of x given that: ∣x + i∣ ≥ (1/x)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}\:\mathrm{given}\:\mathrm{that}:\:\:\:\:\:\mid\mathrm{x}\:+\:\mathrm{i}\mid\:\geqslant\:\frac{\mathrm{1}}{\mathrm{x}} \\ $$

Question Number 51673 Answers: 0 Comments: 1

Question Number 51643 Answers: 2 Comments: 0

If ∣z∣ = 1, prove that ((z − 1)/(z^− − 1)) (z ≠ 1) is a pure imaginary

$$\mathrm{If}\:\:\:\mid\mathrm{z}\mid\:=\:\mathrm{1},\:\:\:\:\mathrm{prove}\:\mathrm{that}\:\:\:\:\:\frac{\mathrm{z}\:−\:\mathrm{1}}{\overset{−} {\mathrm{z}}\:−\:\mathrm{1}}\:\:\:\:\:\:\left(\mathrm{z}\:\neq\:\mathrm{1}\right)\:\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{pure}\:\mathrm{imaginary} \\ $$

Question Number 51630 Answers: 1 Comments: 4

Question Number 51628 Answers: 0 Comments: 2

Question Number 51621 Answers: 0 Comments: 6

Question Number 51571 Answers: 1 Comments: 0

If α − jβ = (1/(a − jb)) , where α, β, a, b are real, express b in terms of α, β Answer: ((− β)/(α^2 + β^2 − 2α + 1))

$$\mathrm{If}\:\:\:\alpha\:−\:\mathrm{j}\beta\:\:=\:\:\frac{\mathrm{1}}{\mathrm{a}\:−\:\mathrm{jb}}\:\:,\:\:\:\:\:\:\mathrm{where}\:\:\:\alpha,\:\beta,\:\mathrm{a},\:\mathrm{b}\:\:\mathrm{are}\:\mathrm{real},\:\mathrm{express}\:\:\mathrm{b}\:\:\mathrm{in}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\:\alpha,\:\beta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Answer}:\:\:\:\:\:\:\:\:\:\:\frac{−\:\beta}{\alpha^{\mathrm{2}} \:+\:\beta^{\mathrm{2}} \:−\:\mathrm{2}\alpha\:+\:\mathrm{1}} \\ $$

Question Number 51448 Answers: 0 Comments: 3

Question Number 51420 Answers: 2 Comments: 0

∫ (e^(3x) /(1 + e^x )) dx

$$\int\:\:\frac{\mathrm{e}^{\mathrm{3x}} }{\mathrm{1}\:+\:\mathrm{e}^{\mathrm{x}} }\:\mathrm{dx} \\ $$

Question Number 51389 Answers: 1 Comments: 2

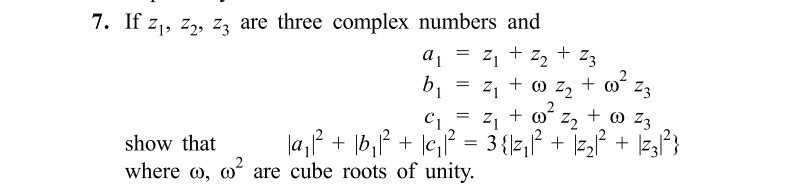
Question Number 51360 Answers: 0 Comments: 0

Question Number 51321 Answers: 1 Comments: 0

A B C D is a parallelogram on the Argand plane. The affixes of A, B, C are 8 + 5i, − 7 − 5i, − 5 + 5i respectively . Find the affix of D

$$\mathrm{A}\:\mathrm{B}\:\mathrm{C}\:\mathrm{D}\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{parallelogram}\:\mathrm{on}\:\mathrm{the}\:\mathrm{Argand}\:\mathrm{plane}.\:\mathrm{The}\: \\ $$$$\mathrm{affixes}\:\mathrm{of}\:\:\mathrm{A},\:\mathrm{B},\:\mathrm{C}\:\:\mathrm{are}\:\:\:\mathrm{8}\:+\:\mathrm{5i},\:\:−\:\mathrm{7}\:−\:\mathrm{5i},\:\:−\:\mathrm{5}\:+\:\mathrm{5i}\:\:\mathrm{respectively} \\ $$$$.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{affix}\:\mathrm{of}\:\:\mathrm{D} \\ $$

Question Number 51320 Answers: 1 Comments: 0

The points A, B, C represent the complex numbers z_1 , z_2 , z_3 respectively. And G is the centroid of the triangle A B C, if 4z_1 + z_2 + z_3 = 0, show that the origin is the mid point of AG.

$$\mathrm{The}\:\mathrm{points}\:\mathrm{A},\:\mathrm{B},\:\mathrm{C}\:\:\mathrm{represent}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{numbers}\:\:\mathrm{z}_{\mathrm{1}} ,\:\mathrm{z}_{\mathrm{2}} ,\:\mathrm{z}_{\mathrm{3}} \: \\ $$$$\mathrm{respectively}.\:\mathrm{And}\:\mathrm{G}\:\mathrm{is}\:\mathrm{the}\:\mathrm{centroid}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle}\:\mathrm{A}\:\mathrm{B}\:\mathrm{C},\:\:\mathrm{if} \\ $$$$\mathrm{4z}_{\mathrm{1}} \:+\:\mathrm{z}_{\mathrm{2}} \:+\:\mathrm{z}_{\mathrm{3}} \:\:=\:\:\mathrm{0},\:\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{origin}\:\mathrm{is}\:\mathrm{the}\:\mathrm{mid}\:\mathrm{point}\:\mathrm{of}\:\:\mathrm{AG}. \\ $$

Question Number 51316 Answers: 0 Comments: 2

Question Number 51314 Answers: 0 Comments: 1

Question Number 51312 Answers: 0 Comments: 1

Question Number 51307 Answers: 0 Comments: 3

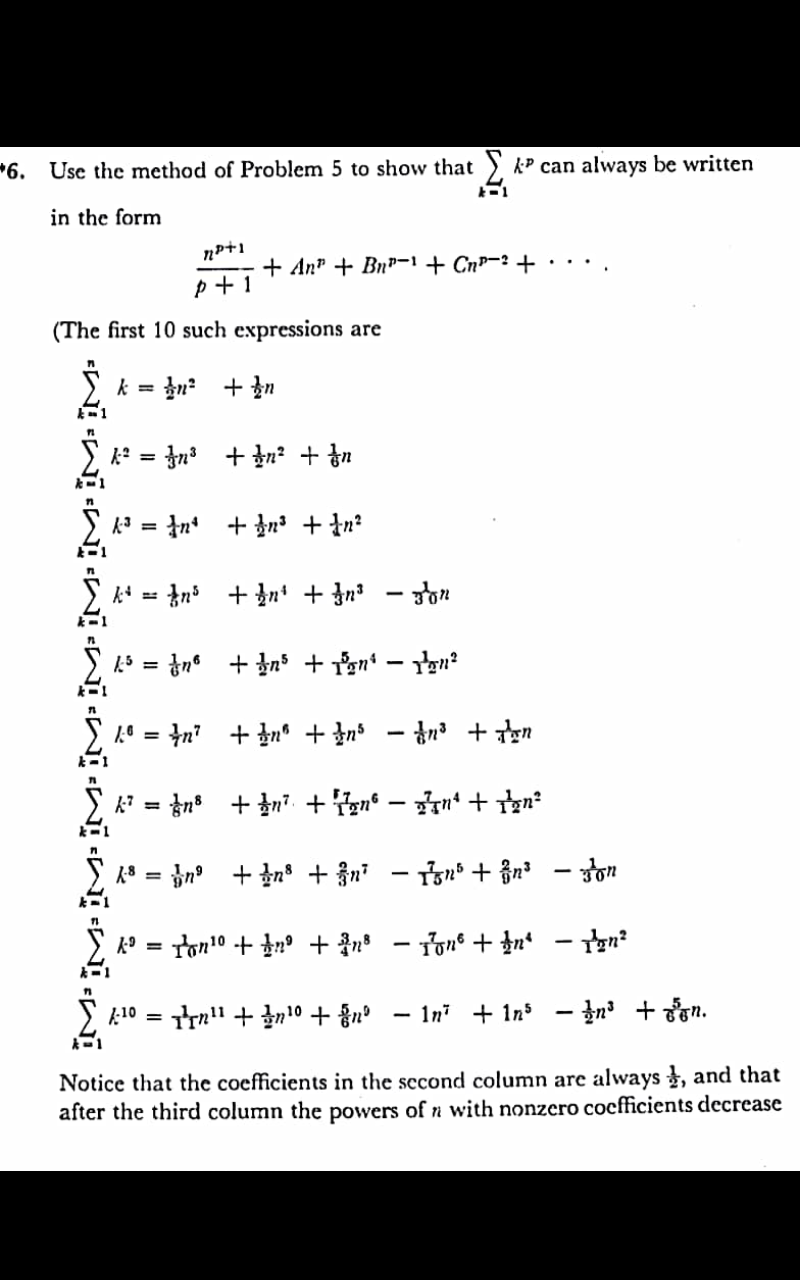
Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103 Pg 104 Pg 105

Contact: info@tinkutara.com