Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 19795 by Tinkutara last updated on 15/Aug/17

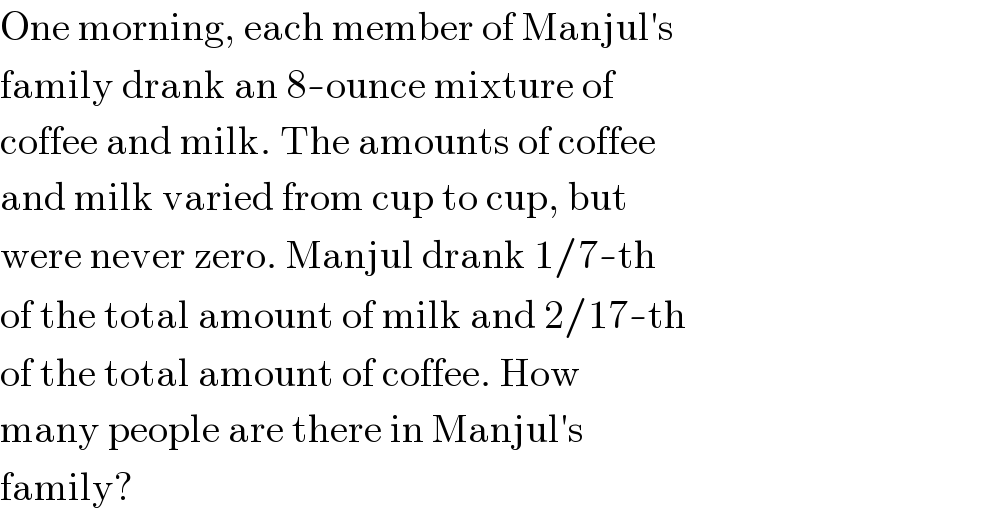
One morning, each member of Manjul′s family drank an 8-ounce mixture of coffee and milk. The amounts of coffee and milk varied from cup to cup, but were never zero. Manjul drank 1/7-th of the total amount of milk and 2/17-th of the total amount of coffee. How many people are there in Manjul′s family?

$$\mathrm{One}\:\mathrm{morning},\:\mathrm{each}\:\mathrm{member}\:\mathrm{of}\:\mathrm{Manjul}'\mathrm{s} \\ $$$$\mathrm{family}\:\mathrm{drank}\:\mathrm{an}\:\mathrm{8}-\mathrm{ounce}\:\mathrm{mixture}\:\mathrm{of} \\ $$$$\mathrm{coffee}\:\mathrm{and}\:\mathrm{milk}.\:\mathrm{The}\:\mathrm{amounts}\:\mathrm{of}\:\mathrm{coffee} \\ $$$$\mathrm{and}\:\mathrm{milk}\:\mathrm{varied}\:\mathrm{from}\:\mathrm{cup}\:\mathrm{to}\:\mathrm{cup},\:\mathrm{but} \\ $$$$\mathrm{were}\:\mathrm{never}\:\mathrm{zero}.\:\mathrm{Manjul}\:\mathrm{drank}\:\mathrm{1}/\mathrm{7}-\mathrm{th} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{total}\:\mathrm{amount}\:\mathrm{of}\:\mathrm{milk}\:\mathrm{and}\:\mathrm{2}/\mathrm{17}-\mathrm{th} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{total}\:\mathrm{amount}\:\mathrm{of}\:\mathrm{coffee}.\:\mathrm{How} \\ $$$$\mathrm{many}\:\mathrm{people}\:\mathrm{are}\:\mathrm{there}\:\mathrm{in}\:\mathrm{Manjul}'\mathrm{s} \\ $$$$\mathrm{family}? \\ $$

Answered by Tinkutara last updated on 19/Aug/17

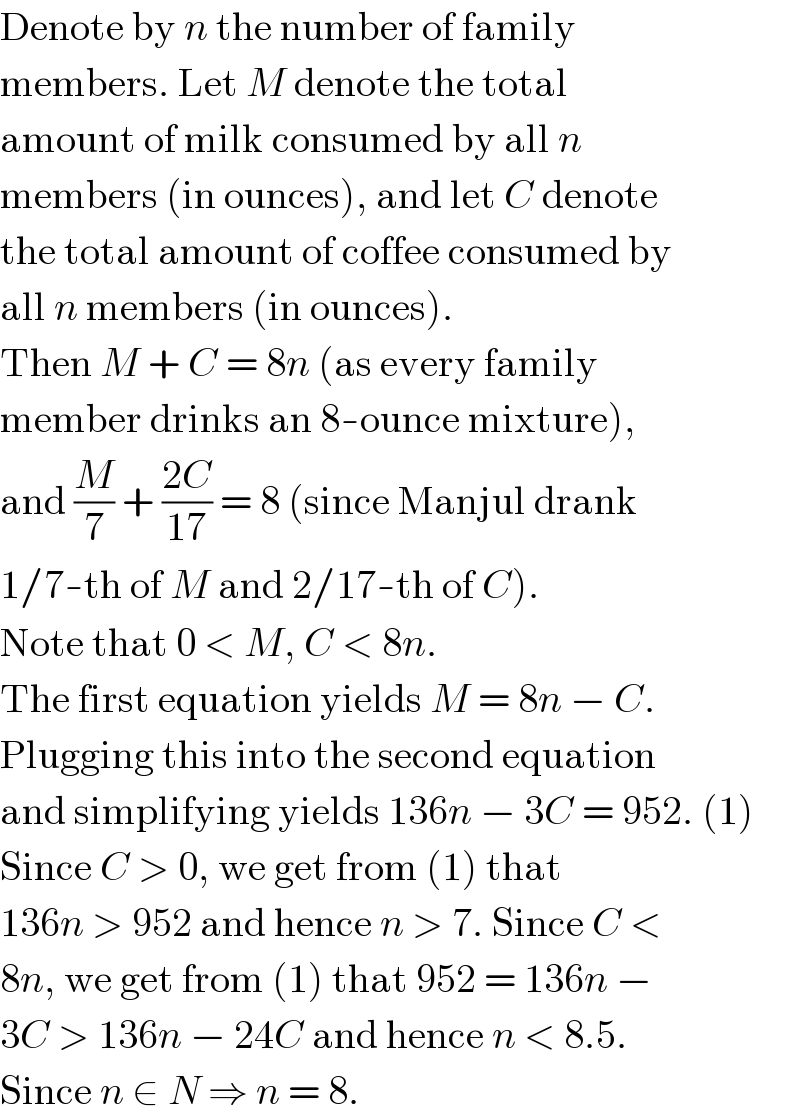
Denote by n the number of family members. Let M denote the total amount of milk consumed by all n members (in ounces), and let C denote the total amount of coffee consumed by all n members (in ounces). Then M + C = 8n (as every family member drinks an 8-ounce mixture), and (M/7) + ((2C)/(17)) = 8 (since Manjul drank 1/7-th of M and 2/17-th of C). Note that 0 < M, C < 8n. The first equation yields M = 8n − C. Plugging this into the second equation and simplifying yields 136n − 3C = 952. (1) Since C > 0, we get from (1) that 136n > 952 and hence n > 7. Since C < 8n, we get from (1) that 952 = 136n − 3C > 136n − 24C and hence n < 8.5. Since n ∈ N ⇒ n = 8.

$$\mathrm{Denote}\:\mathrm{by}\:{n}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{family} \\ $$$$\mathrm{members}.\:\mathrm{Let}\:{M}\:\mathrm{denote}\:\mathrm{the}\:\mathrm{total} \\ $$$$\mathrm{amount}\:\mathrm{of}\:\mathrm{milk}\:\mathrm{consumed}\:\mathrm{by}\:\mathrm{all}\:{n} \\ $$$$\mathrm{members}\:\left(\mathrm{in}\:\mathrm{ounces}\right),\:\mathrm{and}\:\mathrm{let}\:{C}\:\mathrm{denote} \\ $$$$\mathrm{the}\:\mathrm{total}\:\mathrm{amount}\:\mathrm{of}\:\mathrm{coffee}\:\mathrm{consumed}\:\mathrm{by} \\ $$$$\mathrm{all}\:{n}\:\mathrm{members}\:\left(\mathrm{in}\:\mathrm{ounces}\right). \\ $$$$\mathrm{Then}\:{M}\:+\:{C}\:=\:\mathrm{8}{n}\:\left(\mathrm{as}\:\mathrm{every}\:\mathrm{family}\right. \\ $$$$\left.\mathrm{member}\:\mathrm{drinks}\:\mathrm{an}\:\mathrm{8}-\mathrm{ounce}\:\mathrm{mixture}\right), \\ $$$$\mathrm{and}\:\frac{{M}}{\mathrm{7}}\:+\:\frac{\mathrm{2}{C}}{\mathrm{17}}\:=\:\mathrm{8}\:\left(\mathrm{since}\:\mathrm{Manjul}\:\mathrm{drank}\right. \\ $$$$\left.\mathrm{1}/\mathrm{7}-\mathrm{th}\:\mathrm{of}\:{M}\:\mathrm{and}\:\mathrm{2}/\mathrm{17}-\mathrm{th}\:\mathrm{of}\:{C}\right). \\ $$$$\mathrm{Note}\:\mathrm{that}\:\mathrm{0}\:<\:{M},\:{C}\:<\:\mathrm{8}{n}. \\ $$$$\mathrm{The}\:\mathrm{first}\:\mathrm{equation}\:\mathrm{yields}\:{M}\:=\:\mathrm{8}{n}\:−\:{C}. \\ $$$$\mathrm{Plugging}\:\mathrm{this}\:\mathrm{into}\:\mathrm{the}\:\mathrm{second}\:\mathrm{equation} \\ $$$$\mathrm{and}\:\mathrm{simplifying}\:\mathrm{yields}\:\mathrm{136}{n}\:−\:\mathrm{3}{C}\:=\:\mathrm{952}.\:\left(\mathrm{1}\right) \\ $$$$\mathrm{Since}\:{C}\:>\:\mathrm{0},\:\mathrm{we}\:\mathrm{get}\:\mathrm{from}\:\left(\mathrm{1}\right)\:\mathrm{that} \\ $$$$\mathrm{136}{n}\:>\:\mathrm{952}\:\mathrm{and}\:\mathrm{hence}\:{n}\:>\:\mathrm{7}.\:\mathrm{Since}\:{C}\:< \\ $$$$\mathrm{8}{n},\:\mathrm{we}\:\mathrm{get}\:\mathrm{from}\:\left(\mathrm{1}\right)\:\mathrm{that}\:\mathrm{952}\:=\:\mathrm{136}{n}\:− \\ $$$$\mathrm{3}{C}\:>\:\mathrm{136}{n}\:−\:\mathrm{24}{C}\:\mathrm{and}\:\mathrm{hence}\:{n}\:<\:\mathrm{8}.\mathrm{5}. \\ $$$$\mathrm{Since}\:{n}\:\in\:{N}\:\Rightarrow\:{n}\:=\:\mathrm{8}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com