
Question Number 23864 by Tinkutara last updated on 08/Nov/17

$$\mathrm{One}\:\mathrm{mole}\:\mathrm{of}\:\mathrm{steam}\:\mathrm{is}\:\mathrm{condensed}\:\mathrm{at} \\ $$$$\mathrm{100}°\mathrm{C},\:\mathrm{the}\:\mathrm{water}\:\mathrm{is}\:\mathrm{cooled}\:\mathrm{to}\:\mathrm{0}°\mathrm{C}\:\mathrm{and} \\ $$$$\mathrm{frozen}\:\mathrm{to}\:\mathrm{ice}.\:\mathrm{Which}\:\mathrm{of}\:\mathrm{the}\:\mathrm{following} \\ $$$$\mathrm{statements}\:\mathrm{are}\:\mathrm{correct},\:\mathrm{given}\:\mathrm{heat}\:\mathrm{of} \\ $$$$\mathrm{vapourization}\:\mathrm{and}\:\mathrm{fusion}\:\mathrm{are}\:\mathrm{540}\:\mathrm{cal}/ \\ $$$$\mathrm{gm}\:\mathrm{and}\:\mathrm{80}\:\mathrm{cal}/\mathrm{gm}?\:\left(\mathrm{average}\:\mathrm{heat}\right. \\ $$$$\mathrm{capacity}\:\mathrm{of}\:\mathrm{liquid}\:\mathrm{water}\:=\:\mathrm{1}\:\mathrm{cal}\:\mathrm{gm}^{−\mathrm{1}} \\ $$$$\left.\mathrm{degree}^{−\mathrm{1}} \right) \\ $$$$\left(\mathrm{1}\right)\:\mathrm{Entropy}\:\mathrm{change}\:\mathrm{during}\:\mathrm{the} \\ $$$$\mathrm{condensation}\:\mathrm{of}\:\mathrm{steam}\:\mathrm{is}\:−\mathrm{26}.\mathrm{06}\:\mathrm{cal}/°\mathrm{C} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{Entropy}\:\mathrm{change}\:\mathrm{during}\:\mathrm{cooling}\:\mathrm{of} \\ $$$$\mathrm{water}\:\mathrm{from}\:\mathrm{100}°\mathrm{C}\:\mathrm{to}\:\mathrm{0}°\mathrm{C}\:\mathrm{is}\:−\mathrm{5}.\mathrm{62}\:\mathrm{cal}/°\mathrm{C} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{Entropy}\:\mathrm{change}\:\mathrm{during}\:\mathrm{freezing}\:\mathrm{of} \\ $$$$\mathrm{water}\:\mathrm{at}\:\mathrm{0}°\mathrm{C}\:\mathrm{is}\:−\mathrm{5}.\mathrm{27}\:\mathrm{cal}/°\mathrm{C} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{Total}\:\mathrm{entropy}\:\mathrm{change}\:\mathrm{is}\:−\mathrm{36}.\mathrm{95} \\ $$$$\mathrm{cal}/°\mathrm{C} \\ $$
Answered by ajfour last updated on 09/Nov/17
![All correct (I believe). ∫dS = ∫ (dQ/T) . during conensation T=373K (constant) ∫dQ=−mL_(vap) So △S_(condensation) =−((18×540)/(373)) (J/K) =−26.06 J/K △S_(cooling) =∫_(373) ^( 273) ((mc dT)/T) =−18ln (((373)/(273))) ≈ −18ln (((124.3)/(91))) ≈−18×2.303×(3log 5−2log 3−1) ≈ −18×2.3×[3(1−0.3010)−2×0.4771−1] ≈ −18×2.3[2.1−1.9542] ≈ −18×2.3×0.145 ≈ −9×2.3×0.29= 20.7×0.29 J/K ≈−6 J/K . △S_(freezing) =−((mL_(fusion) )/T_f ) =((−18×80)/(273)) = −5.27 J/K △S_(net) =−(26+6+5.3)J/K =−37.3 J/K .](Q23875.png)
$${All}\:{correct}\:\left({I}\:{believe}\right).\:\: \\ $$$$\:\:\:\int{dS}\:=\:\int\:\frac{{dQ}}{{T}}\:. \\ $$$${during}\:{conensation} \\ $$$${T}=\mathrm{373}{K}\:\:\left({constant}\right) \\ $$$$\int{dQ}=−{mL}_{{vap}} \\ $$$${So}\:\:\:\bigtriangleup{S}_{{condensation}} =−\frac{\mathrm{18}×\mathrm{540}}{\mathrm{373}}\:\frac{{J}}{{K}} \\ $$$$\:\:\:\:=−\mathrm{26}.\mathrm{06}\:{J}/{K} \\ $$$$\bigtriangleup{S}_{{cooling}} =\int_{\mathrm{373}} ^{\:\:\mathrm{273}} \:\:\frac{{mc}\:{dT}}{{T}} \\ $$$$\:\:\:=−\mathrm{18ln}\:\left(\frac{\mathrm{373}}{\mathrm{273}}\right)\:\approx\:−\mathrm{18ln}\:\left(\frac{\mathrm{124}.\mathrm{3}}{\mathrm{91}}\right) \\ $$$$\:\:\:\approx−\mathrm{18}×\mathrm{2}.\mathrm{303}×\left(\mathrm{3log}\:\mathrm{5}−\mathrm{2log}\:\mathrm{3}−\mathrm{1}\right)\: \\ $$$$\:\:\approx\:−\mathrm{18}×\mathrm{2}.\mathrm{3}×\left[\mathrm{3}\left(\mathrm{1}−\mathrm{0}.\mathrm{3010}\right)−\mathrm{2}×\mathrm{0}.\mathrm{4771}−\mathrm{1}\right] \\ $$$$\approx\:−\mathrm{18}×\mathrm{2}.\mathrm{3}\left[\mathrm{2}.\mathrm{1}−\mathrm{1}.\mathrm{9542}\right] \\ $$$$\approx\:−\mathrm{18}×\mathrm{2}.\mathrm{3}×\mathrm{0}.\mathrm{145} \\ $$$$\approx\:−\mathrm{9}×\mathrm{2}.\mathrm{3}×\mathrm{0}.\mathrm{29}=\:\mathrm{20}.\mathrm{7}×\mathrm{0}.\mathrm{29}\:{J}/{K}\: \\ $$$$\:\:\:\approx−\mathrm{6}\:{J}/{K}\:. \\ $$$$\bigtriangleup{S}_{{freezing}} =−\frac{{mL}_{{fusion}} }{{T}_{{f}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{−\mathrm{18}×\mathrm{80}}{\mathrm{273}}\:=\:−\mathrm{5}.\mathrm{27}\:{J}/{K} \\ $$$$\bigtriangleup{S}_{{net}} =−\left(\mathrm{26}+\mathrm{6}+\mathrm{5}.\mathrm{3}\right){J}/{K} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{37}.\mathrm{3}\:{J}/{K}\:. \\ $$
Commented by Tinkutara last updated on 09/Nov/17

$${Why}\:{in}\:{calculating}\:\Delta{S}_{{condensation}} {and} \\ $$$$\Delta{S}_{{freezing}} \:{you}\:{have}\:{taken}\:{them}\:{to}\:{be} \\ $$$$−{mL}?\:{Why}\:{not}\:+{mL}?\:{I}\:{know}\:{that} \\ $$$${entropy}\:{decreases}\:{but}\:{in}\:{formula} \\ $$$${there}\:{is}\:{only}\:+\:{sign}. \\ $$
Commented by Tinkutara last updated on 10/Nov/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented by ajfour last updated on 09/Nov/17
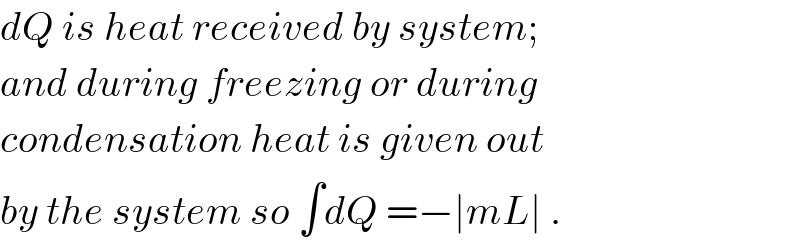
$${dQ}\:{is}\:{heat}\:{received}\:{by}\:{system}; \\ $$$${and}\:{during}\:{freezing}\:{or}\:{during} \\ $$$${condensation}\:{heat}\:{is}\:{given}\:{out} \\ $$$${by}\:{the}\:{system}\:{so}\:\int{dQ}\:=−\mid{mL}\mid\:. \\ $$
