
Question Number 21628 by Tinkutara last updated on 29/Sep/17

$$\mathrm{One}\:\mathrm{end}\:\mathrm{of}\:\mathrm{a}\:\mathrm{massless}\:\mathrm{spring}\:\mathrm{of}\:\mathrm{constant} \\ $$$$\mathrm{100}\:\mathrm{N}/\mathrm{m}\:\mathrm{and}\:\mathrm{natural}\:\mathrm{length}\:\mathrm{0}.\mathrm{5}\:\mathrm{m}\:\mathrm{is} \\ $$$$\mathrm{fixed}\:\mathrm{and}\:\mathrm{the}\:\mathrm{other}\:\mathrm{end}\:\mathrm{is}\:\mathrm{connected}\:\mathrm{to} \\ $$$$\mathrm{a}\:\mathrm{particle}\:\mathrm{of}\:\mathrm{mass}\:\mathrm{0}.\mathrm{5}\:\mathrm{kg}\:\mathrm{lying}\:\mathrm{on}\:\mathrm{a} \\ $$$$\mathrm{frictionless}\:\mathrm{horizontal}\:\mathrm{table}.\:\mathrm{The}\:\mathrm{spring} \\ $$$$\mathrm{remains}\:\mathrm{horizontal}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{mass}\:\mathrm{is}\:\mathrm{made} \\ $$$$\mathrm{to}\:\mathrm{rotate}\:\mathrm{at}\:\mathrm{an}\:\mathrm{angular}\:\mathrm{velocity}\:\mathrm{of}\:\mathrm{2} \\ $$$$\mathrm{rad}/{s},\:\mathrm{find}\:\mathrm{the}\:\mathrm{elongation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{spring}. \\ $$
Answered by ajfour last updated on 30/Sep/17
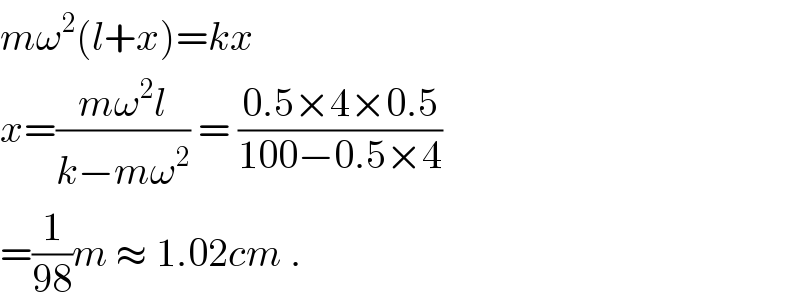
$${m}\omega^{\mathrm{2}} \left({l}+{x}\right)={kx} \\ $$$${x}=\frac{{m}\omega^{\mathrm{2}} {l}}{{k}−{m}\omega^{\mathrm{2}} }\:=\:\frac{\mathrm{0}.\mathrm{5}×\mathrm{4}×\mathrm{0}.\mathrm{5}}{\mathrm{100}−\mathrm{0}.\mathrm{5}×\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{98}}{m}\:\approx\:\mathrm{1}.\mathrm{02}{cm}\:. \\ $$
Commented by Tinkutara last updated on 30/Sep/17
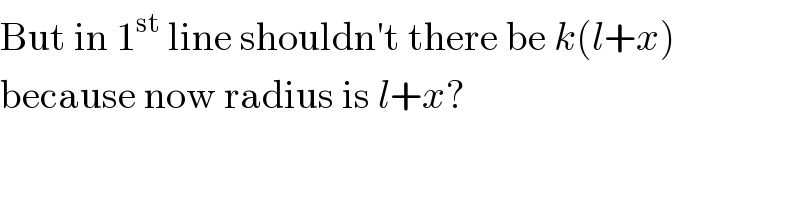
$$\mathrm{But}\:\mathrm{in}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{line}\:\mathrm{shouldn}'\mathrm{t}\:\mathrm{there}\:\mathrm{be}\:{k}\left({l}+{x}\right) \\ $$$$\mathrm{because}\:\mathrm{now}\:\mathrm{radius}\:\mathrm{is}\:{l}+{x}? \\ $$
Commented by ajfour last updated on 30/Sep/17
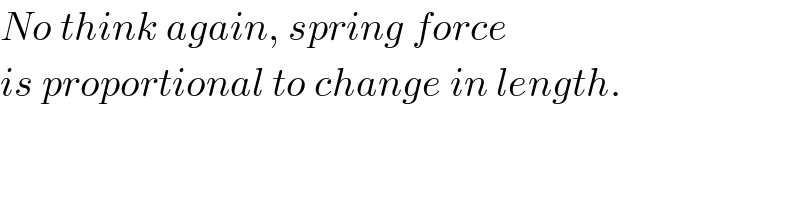
$${No}\:{think}\:{again},\:{spring}\:{force} \\ $$$${is}\:{proportional}\:{to}\:{change}\:{in}\:{length}. \\ $$
Commented by Tinkutara last updated on 30/Sep/17
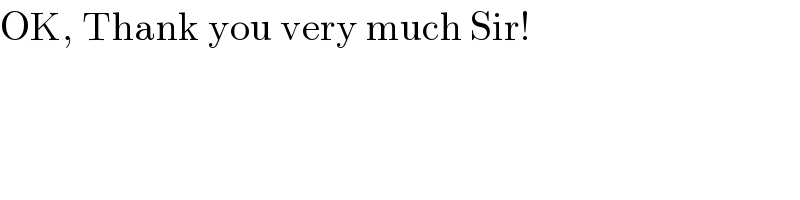
$$\mathrm{OK},\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
