
Question Number 20425 by Tinkutara last updated on 27/Aug/17

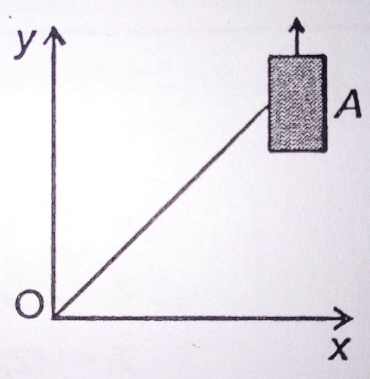
$$\mathrm{On}\:\mathrm{a}\:\mathrm{frictionless}\:\mathrm{horizontal}\:\mathrm{surface}, \\ $$$$\mathrm{assumed}\:\mathrm{to}\:\mathrm{be}\:\mathrm{the}\:{x}-{y}\:\mathrm{plane},\:\mathrm{a}\:\mathrm{small} \\ $$$$\mathrm{trolley}\:{A}\:\mathrm{is}\:\mathrm{moving}\:\mathrm{along}\:\mathrm{a}\:\mathrm{straight} \\ $$$$\mathrm{line}\:\mathrm{parallel}\:\mathrm{to}\:\mathrm{the}\:{y}-\mathrm{axis}\:\left(\mathrm{see}\:\mathrm{figure}\right) \\ $$$$\mathrm{with}\:\mathrm{a}\:\mathrm{constant}\:\mathrm{velocity}\:\mathrm{of}\:\left(\sqrt{\mathrm{3}}\:−\:\mathrm{1}\right)\:\mathrm{m}/\mathrm{s}. \\ $$$$\mathrm{At}\:\mathrm{a}\:\mathrm{particular}\:\mathrm{instant},\:\mathrm{when}\:\mathrm{the}\:\mathrm{line} \\ $$$${OA}\:\mathrm{makes}\:\mathrm{an}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{45}°\:\mathrm{with}\:\mathrm{the} \\ $$$${x}-\mathrm{axis},\:\mathrm{a}\:\mathrm{ball}\:\mathrm{is}\:\mathrm{thrown}\:\mathrm{along}\:\mathrm{the} \\ $$$$\mathrm{surface}\:\mathrm{from}\:\mathrm{the}\:\mathrm{origin}\:{O}.\:\mathrm{Its}\:\mathrm{velocity} \\ $$$$\mathrm{makes}\:\mathrm{an}\:\mathrm{angle}\:\phi\:\mathrm{with}\:{x}-\mathrm{axis}\:\mathrm{and}\:\mathrm{it} \\ $$$$\mathrm{hits}\:\mathrm{the}\:\mathrm{trolley}. \\ $$$$\mathrm{1}.\:\mathrm{The}\:\mathrm{motion}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ball}\:\mathrm{is}\:\mathrm{observed}\:\mathrm{from} \\ $$$$\mathrm{the}\:\mathrm{frame}\:\mathrm{of}\:\mathrm{the}\:\mathrm{trolley}.\:\mathrm{Calculate}\:\mathrm{the} \\ $$$$\mathrm{angle}\:\theta\:\mathrm{made}\:\mathrm{by}\:\mathrm{the}\:\mathrm{velocity}\:\mathrm{vector}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{ball}\:\mathrm{with}\:\mathrm{the}\:{x}-\mathrm{axis}\:\mathrm{in}\:\mathrm{this}\:\mathrm{frame}. \\ $$$$\mathrm{2}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ball}\:\mathrm{with} \\ $$$$\mathrm{respect}\:\mathrm{to}\:\mathrm{the}\:\mathrm{surface},\:\mathrm{if}\:\phi\:=\:\frac{\mathrm{4}\theta}{\mathrm{3}} \\ $$
Commented by Tinkutara last updated on 26/Aug/17
Answered by ajfour last updated on 28/Aug/17
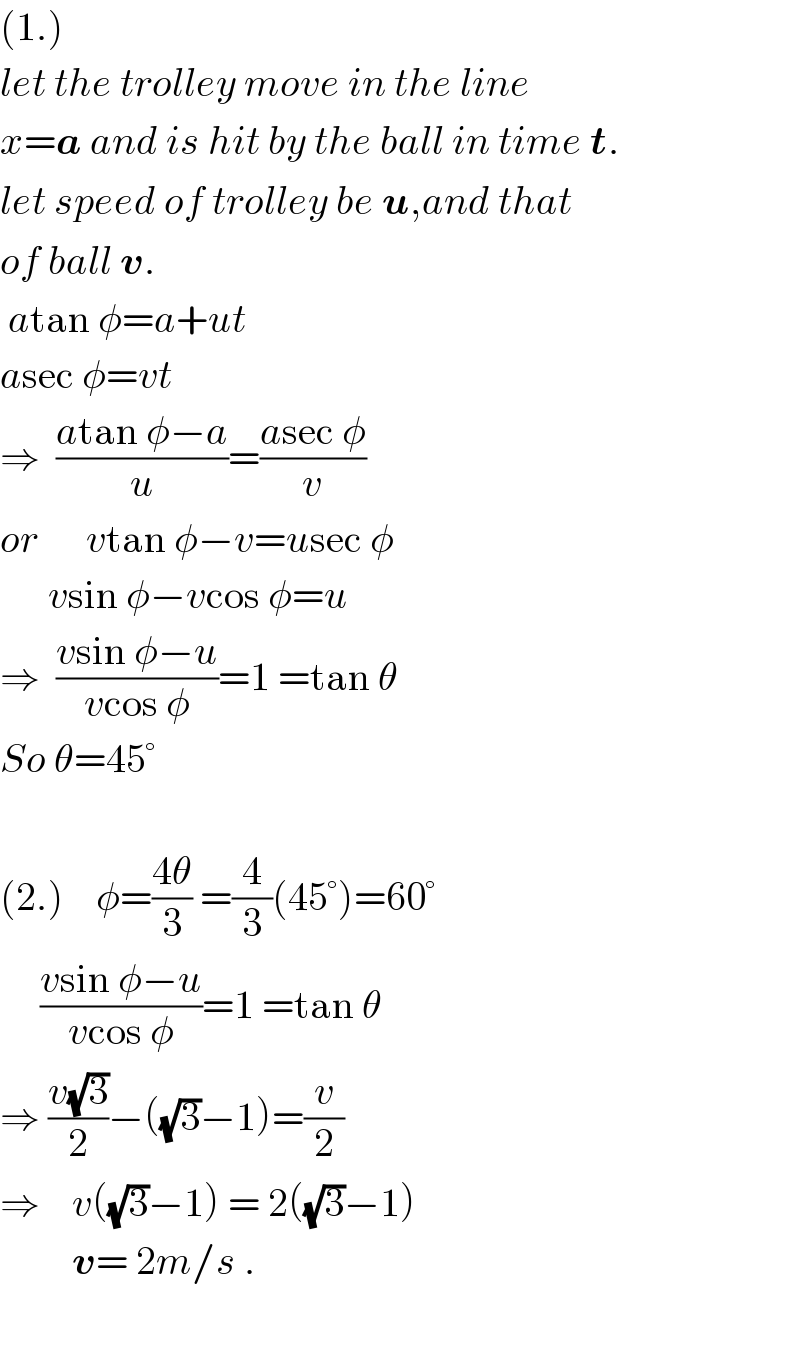
$$\left(\mathrm{1}.\right) \\ $$$${let}\:{the}\:{trolley}\:{move}\:{in}\:{the}\:{line} \\ $$$${x}=\boldsymbol{{a}}\:{and}\:{is}\:{hit}\:{by}\:{the}\:{ball}\:{in}\:{time}\:\boldsymbol{{t}}. \\ $$$${let}\:{speed}\:{of}\:{trolley}\:{be}\:\boldsymbol{{u}},{and}\:{that} \\ $$$${of}\:{ball}\:\boldsymbol{{v}}. \\ $$$$\:{a}\mathrm{tan}\:\phi={a}+{ut} \\ $$$${a}\mathrm{sec}\:\phi={vt} \\ $$$$\Rightarrow\:\:\frac{{a}\mathrm{tan}\:\phi−{a}}{{u}}=\frac{{a}\mathrm{sec}\:\phi}{{v}} \\ $$$${or}\:\:\:\:\:\:{v}\mathrm{tan}\:\phi−{v}={u}\mathrm{sec}\:\phi \\ $$$$\:\:\:\:\:\:{v}\mathrm{sin}\:\phi−{v}\mathrm{cos}\:\phi={u} \\ $$$$\Rightarrow\:\:\frac{{v}\mathrm{sin}\:\phi−{u}}{{v}\mathrm{cos}\:\phi}=\mathrm{1}\:=\mathrm{tan}\:\theta\: \\ $$$${So}\:\theta=\mathrm{45}°\: \\ $$$$ \\ $$$$\left(\mathrm{2}.\right)\:\:\:\:\phi=\frac{\mathrm{4}\theta}{\mathrm{3}}\:=\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{45}°\right)=\mathrm{60}° \\ $$$$\:\:\:\:\:\frac{{v}\mathrm{sin}\:\phi−{u}}{{v}\mathrm{cos}\:\phi}=\mathrm{1}\:=\mathrm{tan}\:\theta\: \\ $$$$\Rightarrow\:\frac{{v}\sqrt{\mathrm{3}}}{\mathrm{2}}−\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)=\frac{{v}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:{v}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\:=\:\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{v}}=\:\mathrm{2}{m}/{s}\:. \\ $$$$ \\ $$
Commented by Tinkutara last updated on 26/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented by Tinkutara last updated on 28/Aug/17

$$\mathrm{Thank}\:\mathrm{you}! \\ $$
