Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 134960 by bobhans last updated on 09/Mar/21

Number theory A palindrome is a number that reads the same backwards as forwards, as 3141413. (a)How many two-digit palindromes are there? (b)How many three-digit ones? (c)How many k-digits ones?

$$\mathrm{Number}\:\mathrm{theory} \\ $$A palindrome is a number that reads the same backwards as forwards, as 3141413. (a)How many two-digit palindromes are there? (b)How many three-digit ones? (c)How many k-digits ones?

Answered by mr W last updated on 09/Mar/21

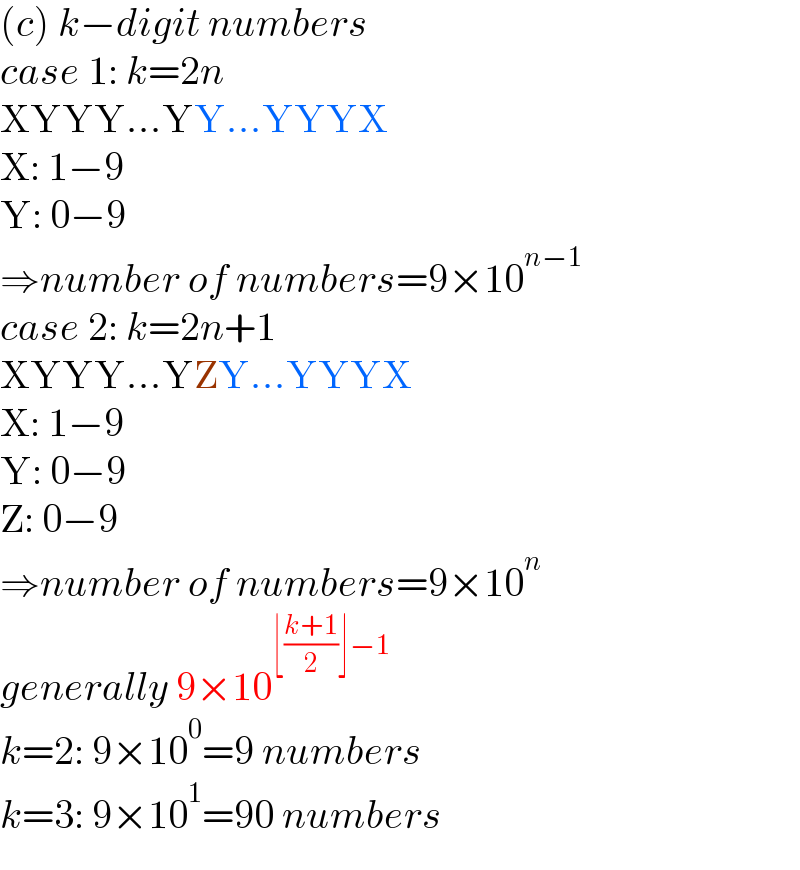
(c) k−digit numbers case 1: k=2n XYYY...YY...YYYX X: 1−9 Y: 0−9 ⇒number of numbers=9×10^(n−1) case 2: k=2n+1 XYYY...YZY...YYYX X: 1−9 Y: 0−9 Z: 0−9 ⇒number of numbers=9×10^n generally 9×10^(⌊((k+1)/2)⌋−1) k=2: 9×10^0 =9 numbers k=3: 9×10^1 =90 numbers

$$\left({c}\right)\:{k}−{digit}\:{numbers} \\ $$$${case}\:\mathrm{1}:\:{k}=\mathrm{2}{n} \\ $$$$\mathrm{XYYY}...\mathrm{YY}...\mathrm{YYYX} \\ $$$$\mathrm{X}:\:\mathrm{1}−\mathrm{9} \\ $$$$\mathrm{Y}:\:\mathrm{0}−\mathrm{9} \\ $$$$\Rightarrow{number}\:{of}\:{numbers}=\mathrm{9}×\mathrm{10}^{{n}−\mathrm{1}} \\ $$$${case}\:\mathrm{2}:\:{k}=\mathrm{2}{n}+\mathrm{1} \\ $$$$\mathrm{XYYY}...\mathrm{YZY}...\mathrm{YYYX} \\ $$$$\mathrm{X}:\:\mathrm{1}−\mathrm{9} \\ $$$$\mathrm{Y}:\:\mathrm{0}−\mathrm{9} \\ $$$$\mathrm{Z}:\:\mathrm{0}−\mathrm{9} \\ $$$$\Rightarrow{number}\:{of}\:{numbers}=\mathrm{9}×\mathrm{10}^{{n}} \\ $$$${generally}\:\mathrm{9}×\mathrm{10}^{\lfloor\frac{{k}+\mathrm{1}}{\mathrm{2}}\rfloor−\mathrm{1}} \\ $$$${k}=\mathrm{2}:\:\mathrm{9}×\mathrm{10}^{\mathrm{0}} =\mathrm{9}\:{numbers} \\ $$$${k}=\mathrm{3}:\:\mathrm{9}×\mathrm{10}^{\mathrm{1}} =\mathrm{90}\:{numbers} \\ $$

Commented by Rasheed.Sindhi last updated on 09/Mar/21

Wonderful sir!

$$\mathcal{W}{onderful}\:\:\boldsymbol{{sir}}! \\ $$

Commented by mr W last updated on 09/Mar/21

thanks sir!

$${thanks}\:{sir}! \\ $$

Commented by mr W last updated on 09/Mar/21

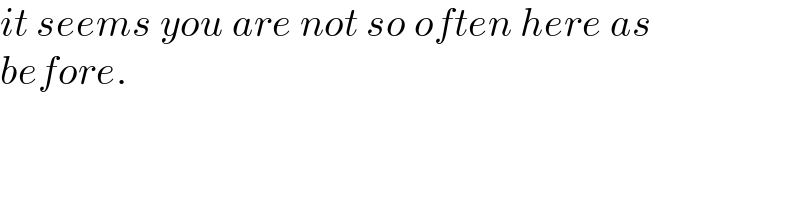
it seems you are not so often here as before.

$${it}\:{seems}\:{you}\:{are}\:{not}\:{so}\:{often}\:{here}\:{as} \\ $$$${before}. \\ $$

Commented by Rasheed.Sindhi last updated on 09/Mar/21

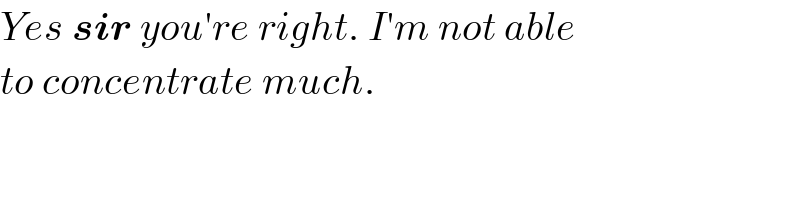
Yes sir you′re right. I′m not able to concentrate much.

$${Yes}\:\boldsymbol{{sir}}\:{you}'{re}\:{right}.\:{I}'{m}\:{not}\:{able} \\ $$$${to}\:{concentrate}\:{much}. \\ $$

Commented by bobhans last updated on 09/Mar/21

yess

$$\mathrm{yess} \\ $$

Commented by liberty last updated on 09/Mar/21

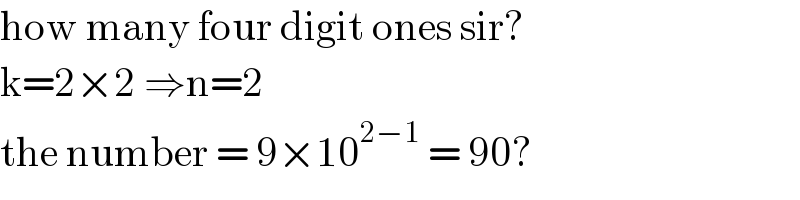
how many four digit ones sir? k=2×2 ⇒n=2 the number = 9×10^(2−1) = 90?

$$\mathrm{how}\:\mathrm{many}\:\mathrm{four}\:\mathrm{digit}\:\mathrm{ones}\:\mathrm{sir}? \\ $$$$\mathrm{k}=\mathrm{2}×\mathrm{2}\:\Rightarrow\mathrm{n}=\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{number}\:=\:\mathrm{9}×\mathrm{10}^{\mathrm{2}−\mathrm{1}} \:=\:\mathrm{90}? \\ $$

Commented by mr W last updated on 10/Mar/21

yes

$${yes} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com