Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 206365 by hardmath last updated on 12/Apr/24

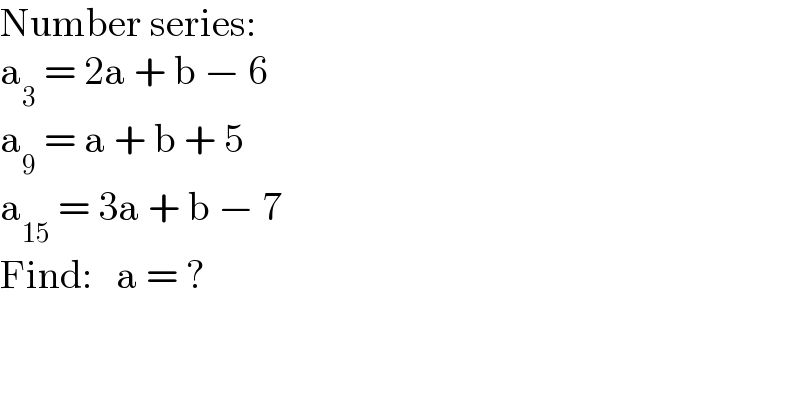
Number series: a_3 = 2a + b − 6 a_9 = a + b + 5 a_(15) = 3a + b − 7 Find: a = ?

$$\mathrm{Number}\:\mathrm{series}: \\ $$$$\mathrm{a}_{\mathrm{3}} \:=\:\mathrm{2a}\:+\:\mathrm{b}\:−\:\mathrm{6} \\ $$$$\mathrm{a}_{\mathrm{9}} \:=\:\mathrm{a}\:+\:\mathrm{b}\:+\:\mathrm{5} \\ $$$$\mathrm{a}_{\mathrm{15}} \:=\:\mathrm{3a}\:+\:\mathrm{b}\:−\:\mathrm{7} \\ $$$$\mathrm{Find}:\:\:\:\mathrm{a}\:=\:? \\ $$

Commented by A5T last updated on 12/Apr/24

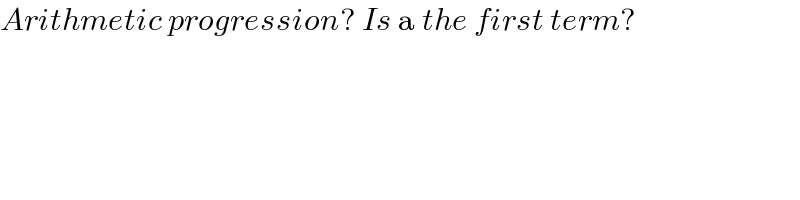
Arithmetic progression? Is a the first term?

$${Arithmetic}\:{progression}?\:{Is}\:\mathrm{a}\:{the}\:{first}\:{term}? \\ $$

Commented by hardmath last updated on 12/Apr/24

yes, arithmetic

$$\mathrm{yes},\:\mathrm{arithmetic} \\ $$

Commented by A5T last updated on 12/Apr/24

Is a the first term?

$${Is}\:\mathrm{a}\:{the}\:{first}\:{term}? \\ $$

Commented by hardmath last updated on 12/Apr/24

yes dear ser

$$\mathrm{yes}\:\mathrm{dear}\:\mathrm{ser} \\ $$

Answered by A5T last updated on 12/Apr/24

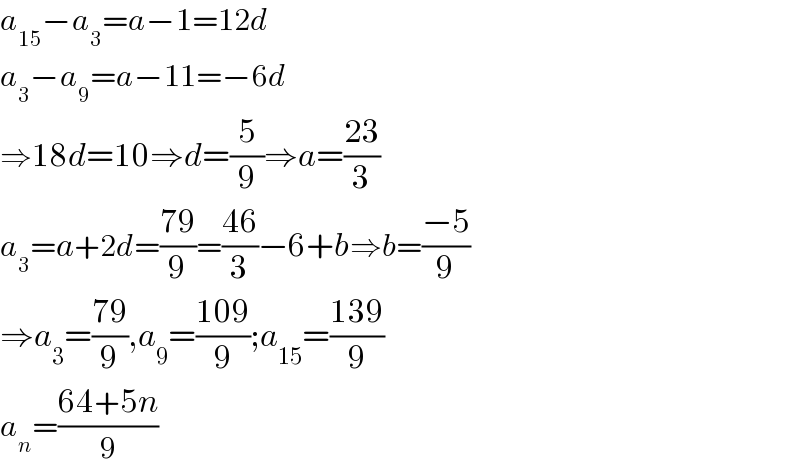
a_(15) −a_3 =a−1=12d a_3 −a_9 =a−11=−6d ⇒18d=10⇒d=(5/9)⇒a=((23)/3) a_3 =a+2d=((79)/9)=((46)/3)−6+b⇒b=((−5)/9) ⇒a_3 =((79)/9),a_9 =((109)/9);a_(15) =((139)/9) a_n =((64+5n)/9)

$${a}_{\mathrm{15}} −{a}_{\mathrm{3}} ={a}−\mathrm{1}=\mathrm{12}{d} \\ $$$${a}_{\mathrm{3}} −{a}_{\mathrm{9}} ={a}−\mathrm{11}=−\mathrm{6}{d} \\ $$$$\Rightarrow\mathrm{18}{d}=\mathrm{10}\Rightarrow{d}=\frac{\mathrm{5}}{\mathrm{9}}\Rightarrow{a}=\frac{\mathrm{23}}{\mathrm{3}} \\ $$$${a}_{\mathrm{3}} ={a}+\mathrm{2}{d}=\frac{\mathrm{79}}{\mathrm{9}}=\frac{\mathrm{46}}{\mathrm{3}}−\mathrm{6}+{b}\Rightarrow{b}=\frac{−\mathrm{5}}{\mathrm{9}} \\ $$$$\Rightarrow{a}_{\mathrm{3}} =\frac{\mathrm{79}}{\mathrm{9}},{a}_{\mathrm{9}} =\frac{\mathrm{109}}{\mathrm{9}};{a}_{\mathrm{15}} =\frac{\mathrm{139}}{\mathrm{9}} \\ $$$${a}_{{n}} =\frac{\mathrm{64}+\mathrm{5}{n}}{\mathrm{9}} \\ $$

Answered by Rasheed.Sindhi last updated on 13/Apr/24

a_n is an AP (given) ∵ 3,9,15 are inAP ∴ a_3 ,a_9 ,a_(15 ) are also in AP ∴ a_9 =((a_3 +a_(15) )/2) a + b + 5=((5a+2b−13)/2) 5a+2b−13=2a+2b+10 3a=23 a=((23)/3)

$$\mathrm{a}_{\mathrm{n}} \:\mathrm{is}\:\mathrm{an}\:\mathrm{AP}\:\left({given}\right) \\ $$$$\because\:\:\mathrm{3},\mathrm{9},\mathrm{15}\:{are}\:{in}\mathrm{AP} \\ $$$$\therefore\:\mathrm{a}_{\mathrm{3}} ,\mathrm{a}_{\mathrm{9}} ,\mathrm{a}_{\mathrm{15}\:} {are}\:{also}\:{in}\:\mathrm{AP} \\ $$$$\therefore\:\mathrm{a}_{\mathrm{9}} =\frac{\mathrm{a}_{\mathrm{3}} +\mathrm{a}_{\mathrm{15}} }{\mathrm{2}} \\ $$$$\mathrm{a}\:+\:\mathrm{b}\:+\:\mathrm{5}=\frac{\mathrm{5a}+\mathrm{2b}−\mathrm{13}}{\mathrm{2}} \\ $$$$\mathrm{5a}+\mathrm{2b}−\mathrm{13}=\mathrm{2a}+\mathrm{2b}+\mathrm{10} \\ $$$$\mathrm{3a}=\mathrm{23} \\ $$$$\mathrm{a}=\frac{\mathrm{23}}{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com