
Previous in Relation and Functions Next in Relation and Functions
Question Number 34029 by rahul 19 last updated on 29/Apr/18
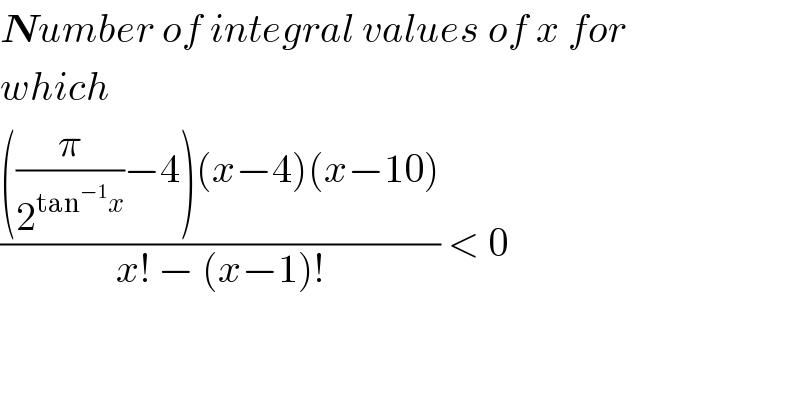
$$\boldsymbol{{N}}{umber}\:{of}\:{integral}\:{values}\:{of}\:{x}\:{for} \\ $$$${which}\: \\ $$$$\frac{\left(\frac{\pi}{\mathrm{2}^{\mathrm{tan}^{−\mathrm{1}} {x}} }−\mathrm{4}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{10}\right)}{{x}!\:−\:\left({x}−\mathrm{1}\right)!}\:<\:\mathrm{0} \\ $$
Commented by rahul 19 last updated on 29/Apr/18
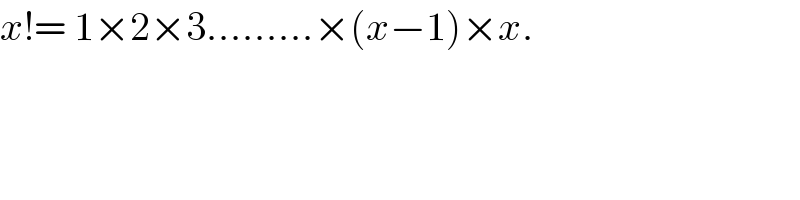
$${x}!=\:\mathrm{1}×\mathrm{2}×\mathrm{3}.........×\left({x}−\mathrm{1}\right)×{x}. \\ $$
Answered by MJS last updated on 29/Apr/18
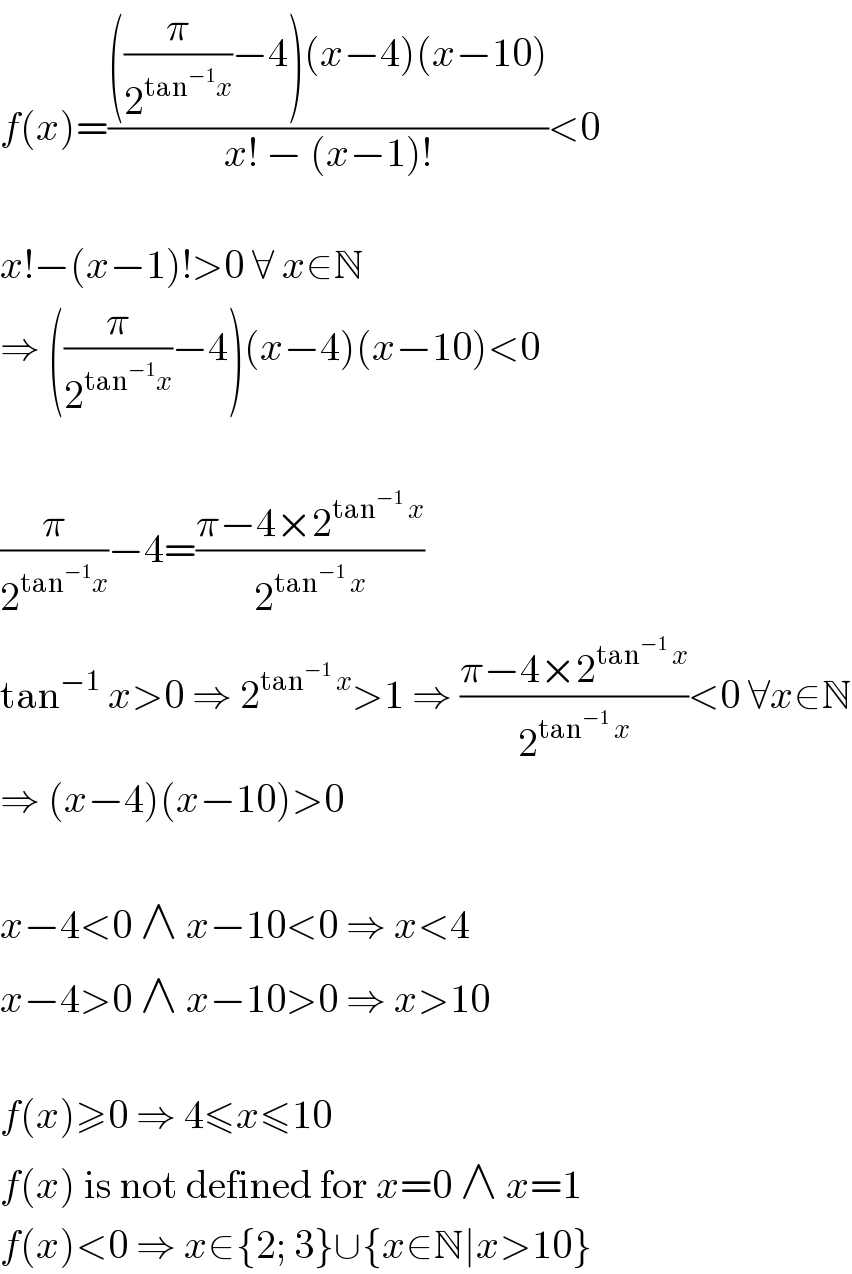
$${f}\left({x}\right)=\frac{\left(\frac{\pi}{\mathrm{2}^{\mathrm{tan}^{−\mathrm{1}} {x}} }−\mathrm{4}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{10}\right)}{{x}!\:−\:\left({x}−\mathrm{1}\right)!}<\mathrm{0} \\ $$$$ \\ $$$${x}!−\left({x}−\mathrm{1}\right)!>\mathrm{0}\:\forall\:{x}\in\mathbb{N} \\ $$$$\Rightarrow\:\left(\frac{\pi}{\mathrm{2}^{\mathrm{tan}^{−\mathrm{1}} {x}} }−\mathrm{4}\right)\left({x}−\mathrm{4}\right)\left({x}−\mathrm{10}\right)<\mathrm{0} \\ $$$$ \\ $$$$\frac{\pi}{\mathrm{2}^{\mathrm{tan}^{−\mathrm{1}} {x}} }−\mathrm{4}=\frac{\pi−\mathrm{4}×\mathrm{2}^{\mathrm{tan}^{−\mathrm{1}} \:{x}} }{\mathrm{2}^{\mathrm{tan}^{−\mathrm{1}} \:{x}} } \\ $$$$\mathrm{tan}^{−\mathrm{1}} \:{x}>\mathrm{0}\:\Rightarrow\:\mathrm{2}^{\mathrm{tan}^{−\mathrm{1}} \:{x}} >\mathrm{1}\:\Rightarrow\:\frac{\pi−\mathrm{4}×\mathrm{2}^{\mathrm{tan}^{−\mathrm{1}} \:{x}} }{\mathrm{2}^{\mathrm{tan}^{−\mathrm{1}} \:{x}} }<\mathrm{0}\:\forall{x}\in\mathbb{N} \\ $$$$\Rightarrow\:\left({x}−\mathrm{4}\right)\left({x}−\mathrm{10}\right)>\mathrm{0} \\ $$$$ \\ $$$${x}−\mathrm{4}<\mathrm{0}\:\wedge\:{x}−\mathrm{10}<\mathrm{0}\:\Rightarrow\:{x}<\mathrm{4} \\ $$$${x}−\mathrm{4}>\mathrm{0}\:\wedge\:{x}−\mathrm{10}>\mathrm{0}\:\Rightarrow\:{x}>\mathrm{10} \\ $$$$ \\ $$$${f}\left({x}\right)\geqslant\mathrm{0}\:\Rightarrow\:\mathrm{4}\leqslant{x}\leqslant\mathrm{10} \\ $$$${f}\left({x}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for}\:{x}=\mathrm{0}\:\wedge\:{x}=\mathrm{1} \\ $$$${f}\left({x}\right)<\mathrm{0}\:\Rightarrow\:{x}\in\left\{\mathrm{2};\:\mathrm{3}\right\}\cup\left\{{x}\in\mathbb{N}\mid{x}>\mathrm{10}\right\} \\ $$
Commented by rahul 19 last updated on 29/Apr/18
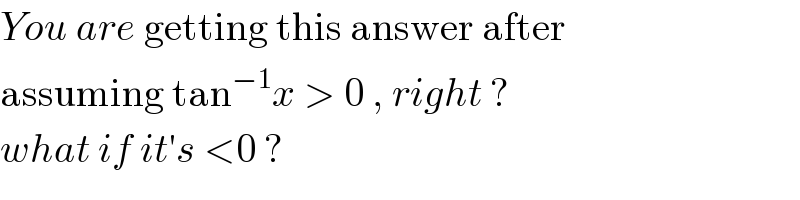
$${You}\:{are}\:\mathrm{getting}\:\mathrm{this}\:\mathrm{answer}\:\mathrm{after}\: \\ $$$$\mathrm{assuming}\:\mathrm{tan}^{−\mathrm{1}} {x}\:>\:\mathrm{0}\:,\:{right}\:? \\ $$$${what}\:{if}\:{it}'{s}\:<\mathrm{0}\:? \\ $$
Commented by MJS last updated on 29/Apr/18
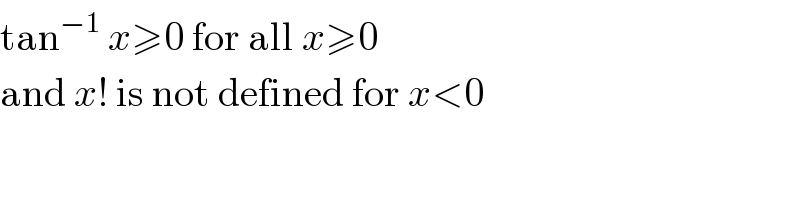
$$\mathrm{tan}^{−\mathrm{1}} \:{x}\geqslant\mathrm{0}\:\mathrm{for}\:\mathrm{all}\:{x}\geqslant\mathrm{0} \\ $$$$\mathrm{and}\:{x}!\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for}\:{x}<\mathrm{0} \\ $$
Commented by rahul 19 last updated on 29/Apr/18

$${Ohh},\:{yes}! \\ $$$$\mathscr{T}{hank}\:{you}\:{sir}. \\ $$
