Question and Answers Forum

Number TheoryQuestion and Answers: Page 8

Question Number 145359 Answers: 1 Comments: 0

How many digits will there be in 875^(16) ?

$$\mathrm{How}\:\mathrm{many}\:\mathrm{digits}\:\mathrm{will}\:\mathrm{there}\:\mathrm{be} \\ $$$$\mathrm{in}\:\mathrm{875}^{\mathrm{16}} \:? \\ $$

Question Number 143790 Answers: 0 Comments: 2

Π_(n=1) ^∞ (1+(x^3 /n^3 ))

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{{x}^{\mathrm{3}} }{{n}^{\mathrm{3}} }\right) \\ $$

Question Number 143085 Answers: 0 Comments: 0

φ(n^4 +1)=8n φ:Euler totient function Solve for n∈N

$$\phi\left({n}^{\mathrm{4}} +\mathrm{1}\right)=\mathrm{8}{n}\:\:\:\:\:\:\phi:{Euler}\:{totient}\:{function} \\ $$$${Solve}\:{for}\:{n}\in\mathbb{N} \\ $$

Question Number 142880 Answers: 1 Comments: 0

Prove that 𝛗(n)=nΠ_k (1−(1/p_k )) φ(n):Euler totient function

$$\:{Prove}\:{that}\:\boldsymbol{\phi}\left({n}\right)={n}\underset{{k}} {\prod}\left(\mathrm{1}−\frac{\mathrm{1}}{{p}_{{k}} }\right)\:\:\phi\left({n}\right):{Euler}\:{totient}\:{function} \\ $$

Question Number 142263 Answers: 0 Comments: 0

(((0 sin(x))),((0 0)) )!+ (((0 sin(2x))),((0 0)) )!+ (((0 sin(3x))),((0 0)) )!+... n^(th) term

$$\begin{pmatrix}{\mathrm{0}\:{sin}\left({x}\right)}\\{\mathrm{0}\:\:\mathrm{0}}\end{pmatrix}!+\begin{pmatrix}{\mathrm{0}\:\:{sin}\left(\mathrm{2}{x}\right)}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}!+\begin{pmatrix}{\mathrm{0}\:\:\:{sin}\left(\mathrm{3}{x}\right)}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}!+...\:{n}^{{th}} \:{term} \\ $$

Question Number 141694 Answers: 0 Comments: 0

log((((√5)+1)/(10))9e^γ )=((ζ(2))/2)(((1^2 +9^2 )/(10^2 )))−((ζ(3))/3) (((1^3 +9^3 )/(10^3 )) )+((ζ(4))/4)(((1^4 +9^4 )/(10^4 )))−... γ=Euler Mascheroni Constant

$${log}\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{10}}\mathrm{9}{e}^{\gamma} \right)=\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{2}}\left(\frac{\mathrm{1}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} }{\mathrm{10}^{\mathrm{2}} }\right)−\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{3}}\:\left(\frac{\mathrm{1}^{\mathrm{3}} +\mathrm{9}^{\mathrm{3}} }{\mathrm{10}^{\mathrm{3}} }\:\right)+\frac{\zeta\left(\mathrm{4}\right)}{\mathrm{4}}\left(\frac{\mathrm{1}^{\mathrm{4}} +\mathrm{9}^{\mathrm{4}} }{\mathrm{10}^{\mathrm{4}} }\right)−... \\ $$$$\gamma={Euler}\:{Mascheroni}\:{Constant} \\ $$

Question Number 140833 Answers: 3 Comments: 1

Determine if the series Σ_(n=1) ^∞ a_n defined by the formula converges or diverges . a_1 = 4 , a_(n+1) = ((10+sin n)/n). a_n

$$\mathrm{Determine}\:\mathrm{if}\:\mathrm{the}\:\mathrm{series}\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\mathrm{a}_{\mathrm{n}} \\ $$$$\mathrm{defined}\:\mathrm{by}\:\mathrm{the}\:\:\mathrm{formula}\:\mathrm{converges}\:\mathrm{or} \\ $$$$\mathrm{diverges}\:.\:\mathrm{a}_{\mathrm{1}} =\:\mathrm{4}\:,\:\mathrm{a}_{\mathrm{n}+\mathrm{1}} \:=\:\frac{\mathrm{10}+\mathrm{sin}\:\mathrm{n}}{\mathrm{n}}.\:\mathrm{a}_{\mathrm{n}} \\ $$

Question Number 140428 Answers: 1 Comments: 1

If 4x=3(Mod 6), find the first four values of x.

$$\mathrm{If}\:\mathrm{4}{x}=\mathrm{3}\left(\mathrm{Mod}\:\mathrm{6}\right),\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{first}\:\mathrm{four}\:\mathrm{values}\:\mathrm{of}\:{x}. \\ $$

Question Number 140329 Answers: 2 Comments: 0

x^(⌊x⌋) + x^(⌈x⌉) = ((175)/8)

$$\:\mathrm{x}^{\lfloor\mathrm{x}\rfloor} \:+\:\mathrm{x}^{\lceil\mathrm{x}\rceil} \:=\:\frac{\mathrm{175}}{\mathrm{8}} \\ $$

Question Number 140449 Answers: 1 Comments: 0

Find the first four values of 2x+5=1(mod 7)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{first}\:\mathrm{four}\:\mathrm{values}\:\mathrm{of} \\ $$$$\mathrm{2}{x}+\mathrm{5}=\mathrm{1}\left(\mathrm{mod}\:\mathrm{7}\right) \\ $$

Question Number 139668 Answers: 1 Comments: 3

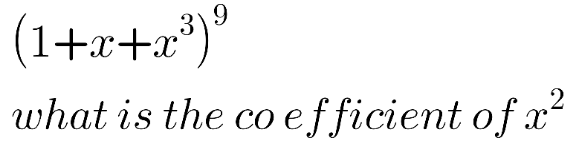
Question Number 139560 Answers: 0 Comments: 0

Σ_(n_1 +2n_2 +3n_3 +..+rn_r =n) ^n (1/(n_1 !n_2 !n_3 !..n_r !1^n_1 2^n_2 3^n_3 4^n_4 ...r^n_r ))=1 0≥n_1 ,n_2 ,n_3 ,..≥n Prove the above identity

$$\underset{{n}_{\mathrm{1}} +\mathrm{2}{n}_{\mathrm{2}} +\mathrm{3}{n}_{\mathrm{3}} +..+{rn}_{{r}} ={n}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{n}_{\mathrm{1}} !{n}_{\mathrm{2}} !{n}_{\mathrm{3}} !..{n}_{{r}} !\mathrm{1}^{{n}_{\mathrm{1}} } \mathrm{2}^{{n}_{\mathrm{2}} } \mathrm{3}^{{n}_{\mathrm{3}} } \mathrm{4}^{{n}_{\mathrm{4}} } ...{r}^{{n}_{{r}} } }=\mathrm{1} \\ $$$$\mathrm{0}\geqslant{n}_{\mathrm{1}} ,{n}_{\mathrm{2}} ,{n}_{\mathrm{3}} ,..\geqslant{n} \\ $$$$\mathrm{P}{rove}\:\mathrm{t}{he}\:{above}\:{identity} \\ $$

Question Number 138003 Answers: 2 Comments: 0

Question Number 137635 Answers: 0 Comments: 1

Question Number 137585 Answers: 2 Comments: 0

Find the cube of the number N= (√(7(√(3(√(7(√(3(√(7(√(3(√(7(√(3...))))))))))))))))

$${Find}\:{the}\:{cube}\:{of}\:{the}\:{number}\: \\ $$$${N}=\:\sqrt{\mathrm{7}\sqrt{\mathrm{3}\sqrt{\mathrm{7}\sqrt{\mathrm{3}\sqrt{\mathrm{7}\sqrt{\mathrm{3}\sqrt{\mathrm{7}\sqrt{\mathrm{3}...}}}}}}}} \\ $$

Question Number 137579 Answers: 1 Comments: 0

(−1)×(1/(π.i)) =?

$$\left(−\mathrm{1}\right)×\frac{\mathrm{1}}{\pi.{i}}\:=?\: \\ $$

Question Number 137383 Answers: 3 Comments: 0

What is the remainder 13^(163) when divided by 99

$${What}\:{is}\:{the}\:{remainder}\:\mathrm{13}^{\mathrm{163}} \:{when} \\ $$$${divided}\:{by}\:\mathrm{99}\: \\ $$

Question Number 137364 Answers: 3 Comments: 0

Find the remainder 7^(30) divide by 10

$${Find}\:{the}\:{remainder}\:\mathrm{7}^{\mathrm{30}} \:{divide} \\ $$$${by}\:\mathrm{10}\: \\ $$

Question Number 136996 Answers: 0 Comments: 0

Given a,b and c is real number satisfy a+b+c = 4 and ab+ac+bc = 3 . The value of ⌈ 3c+2 ⌉ = ?

$$\mathrm{Given}\:\mathrm{a},\mathrm{b}\:\mathrm{and}\:\mathrm{c}\:\mathrm{is}\:\mathrm{real}\:\mathrm{number}\:\mathrm{satisfy} \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{c}\:=\:\mathrm{4}\:\mathrm{and}\:\mathrm{ab}+\mathrm{ac}+\mathrm{bc}\:=\:\mathrm{3}\:.\:\mathrm{The}\:\mathrm{value} \\ $$$$\mathrm{of}\:\lceil\:\mathrm{3c}+\mathrm{2}\:\rceil\:=\:? \\ $$

Question Number 136830 Answers: 1 Comments: 0

Determine all solutions in the integers of the following Diophantine equations: (a)56x+72y=40 (b)24x+138y=18 (c)221x+35y=11

$$ \\ $$Determine all solutions in the integers of the following Diophantine equations: (a)56x+72y=40 (b)24x+138y=18 (c)221x+35y=11

Question Number 136792 Answers: 1 Comments: 0

How do you solve the diophantine equation (1)3xy +2x +y = 12 ? (2) x^3 = 4y^2 +4y−3 ?

$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{diophantine}\:\mathrm{equation} \\ $$$$\left(\mathrm{1}\right)\mathrm{3xy}\:+\mathrm{2x}\:+\mathrm{y}\:=\:\mathrm{12}\:? \\ $$$$\left(\mathrm{2}\right)\:\mathrm{x}^{\mathrm{3}} =\:\mathrm{4y}^{\mathrm{2}} +\mathrm{4y}−\mathrm{3}\:? \\ $$

Question Number 136038 Answers: 0 Comments: 0

Find a_(n ) if (1/z^m )×coth (πz)×cot (zπ)=Σ_(n=0) ^∞ a_n z^n around z=0

$${Find}\:{a}_{{n}\:} {if} \\ $$$$\frac{\mathrm{1}}{{z}^{{m}} }×\mathrm{coth}\:\left(\pi{z}\right)×\mathrm{cot}\:\left({z}\pi\right)=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{a}_{{n}} {z}^{{n}} \\ $$$${around}\:{z}=\mathrm{0} \\ $$

Question Number 135963 Answers: 0 Comments: 0

how many of the first triangular number have the ones zero

$$ \\ $$how many of the first triangular number have the ones zero

Question Number 135958 Answers: 0 Comments: 0

Find the value of n such that ((n(n+1))/2) = k (mod 10) for n is integer number

$${Find}\:{the}\:{value}\:{of}\:{n}\:{such}\:{that} \\ $$$$\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:=\:{k}\:\left({mod}\:\mathrm{10}\right)\:{for} \\ $$$${n}\:{is}\:{integer}\:{number}\: \\ $$

Question Number 135718 Answers: 1 Comments: 0

Question Number 135692 Answers: 1 Comments: 0

Solve the system of congruences 2x≡1(mod5) 3x≡2(mod7) 4x≡1(mod11)

$$ \\ $$Solve the system of congruences 2x≡1(mod5) 3x≡2(mod7) 4x≡1(mod11)

Pg 3 Pg 4 Pg 5 Pg 6 Pg 7 Pg 8 Pg 9 Pg 10 Pg 11 Pg 12

Contact: [email protected]