
Number TheoryQuestion and Answers: Page 7
Question Number 160061 Answers: 1 Comments: 0
Question Number 159925 Answers: 1 Comments: 0
Question Number 159775 Answers: 1 Comments: 0
Question Number 159461 Answers: 0 Comments: 4
Question Number 158914 Answers: 0 Comments: 0
Question Number 158270 Answers: 0 Comments: 0
Question Number 157853 Answers: 0 Comments: 1

Question Number 157219 Answers: 0 Comments: 0
Question Number 156419 Answers: 1 Comments: 1
Question Number 156126 Answers: 1 Comments: 1
Question Number 156201 Answers: 0 Comments: 1
Question Number 155571 Answers: 2 Comments: 0
Question Number 155133 Answers: 2 Comments: 0
Question Number 154672 Answers: 1 Comments: 0
Question Number 153916 Answers: 0 Comments: 0
Question Number 153458 Answers: 0 Comments: 1
Question Number 151265 Answers: 1 Comments: 3

Question Number 150984 Answers: 0 Comments: 0
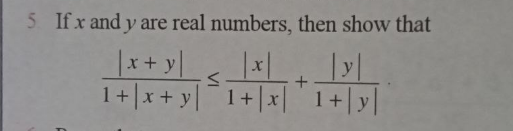
Question Number 150965 Answers: 1 Comments: 0

Question Number 150876 Answers: 0 Comments: 0

Question Number 150223 Answers: 2 Comments: 0

Question Number 149962 Answers: 0 Comments: 0
Question Number 148951 Answers: 2 Comments: 0
Question Number 148211 Answers: 1 Comments: 0

Question Number 145408 Answers: 0 Comments: 0
Question Number 145359 Answers: 1 Comments: 0
