Question and Answers Forum

Number TheoryQuestion and Answers: Page 6

Question Number 167056 Answers: 1 Comments: 0

help me! lim_(x→∞) cosec^(−1) (2)(√(x(√(2(√x)))))

$$\mathrm{help}\:\mathrm{me}!\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}cosec}^{−\mathrm{1}} \left(\mathrm{2}\right)\sqrt{{x}\sqrt{\mathrm{2}\sqrt{{x}}}} \\ $$

Question Number 166994 Answers: 2 Comments: 0

1+1≠??

$$\mathrm{1}+\mathrm{1}\neq?? \\ $$

Question Number 166911 Answers: 1 Comments: 0

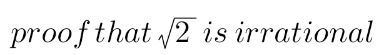
Question Number 166910 Answers: 1 Comments: 1

given that is prime,proof that (√p) is irrational

$${given}\:{that}\:{is}\:{prime},{proof}\:{that}\:\sqrt{{p}}\:{is}\: \\ $$$${irrational} \\ $$

Question Number 166881 Answers: 0 Comments: 0

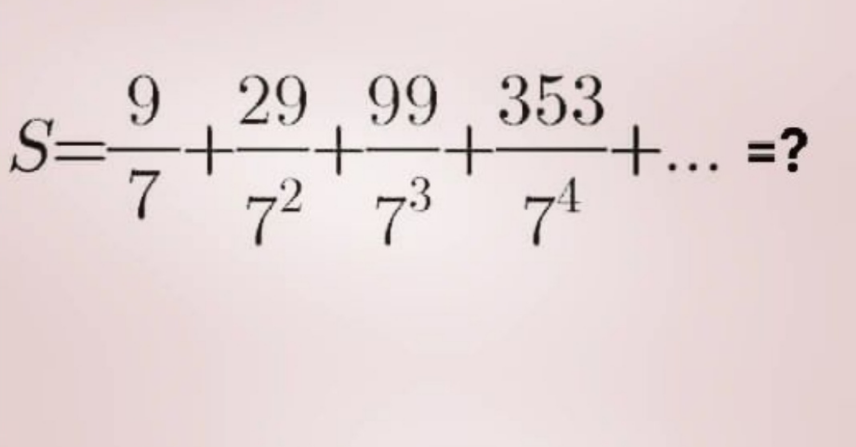
Question Number 166602 Answers: 0 Comments: 0

Determine condition/s that a number divisible by 11 is a palindrome-number.

$$\mathcal{D}{etermine}\:{condition}/{s}\:{that} \\ $$$${a}\:\boldsymbol{{number}}\:\boldsymbol{{divisible}}\:\boldsymbol{{by}}\:\mathrm{11} \\ $$$${is}\:{a}\:\boldsymbol{{palindrome}}-\boldsymbol{{number}}. \\ $$

Question Number 166601 Answers: 0 Comments: 0

What is the condition that a palindrome-number is divisible by 11?

$${What}\:{is}\:{the}\:{condition}\:{that}\: \\ $$$${a}\:\boldsymbol{{palindrome}}-\boldsymbol{{number}} \\ $$$$\:{is}\:\boldsymbol{{divisible}}\:\boldsymbol{{by}}\:\mathrm{11}? \\ $$

Question Number 166530 Answers: 1 Comments: 0

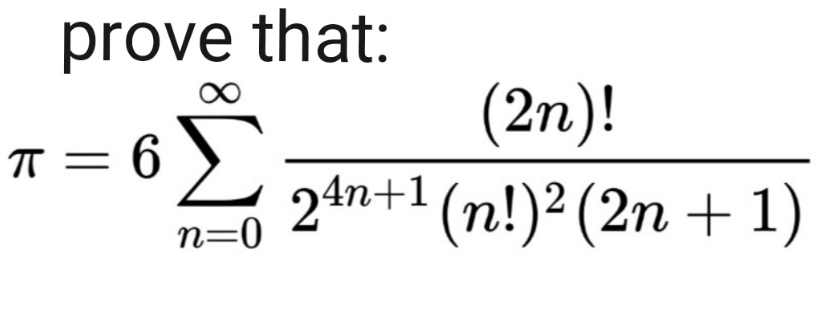
Question Number 166475 Answers: 2 Comments: 5

Find out n∈N such that n^2 +n is divisible by 30.

$$\mathcal{F}{ind}\:{out}\:{n}\in\mathbb{N} \\ $$$$\:{such}\:{that} \\ $$$${n}^{\mathrm{2}} +{n}\:{is}\:{divisible}\:{by}\:\mathrm{30}. \\ $$

Question Number 164940 Answers: 0 Comments: 1

−−−−−−−−− 1!−2!+3!−4!+5!−…−14!+15!=? −−−−−−−−−−by M.A

$$−−−−−−−−− \\ $$$$\mathrm{1}!−\mathrm{2}!+\mathrm{3}!−\mathrm{4}!+\mathrm{5}!−\ldots−\mathrm{14}!+\mathrm{15}!=? \\ $$$$ \\ $$$$−−−−−−−−−−\boldsymbol{{by}}\:\boldsymbol{{M}}.\boldsymbol{{A}} \\ $$

Question Number 164279 Answers: 3 Comments: 0

x^n =n^x x=?

$${x}^{{n}} ={n}^{{x}} \:\:\:{x}=? \\ $$

Question Number 163763 Answers: 3 Comments: 1

$$ \\ $$

Question Number 163662 Answers: 1 Comments: 1

Question Number 163397 Answers: 0 Comments: 5

Question Number 163300 Answers: 1 Comments: 0

∫_0 ^2 f(x)dx⋍f(a)+f(2−a) For what values of a is the following formula accurate for polynomials of degree 3?

$$\int_{\mathrm{0}} ^{\mathrm{2}} \boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}\backsimeq\boldsymbol{{f}}\left(\boldsymbol{{a}}\right)+\boldsymbol{{f}}\left(\mathrm{2}−\boldsymbol{{a}}\right) \\ $$$$ \\ $$For what values of a is the following formula accurate for polynomials of degree 3?

Question Number 163168 Answers: 2 Comments: 1

Question Number 162674 Answers: 2 Comments: 0

Question Number 162169 Answers: 2 Comments: 0

determinant ((( determinant ((( x+y+x^2 y^2 =586_(x=?,y=? ) ^(x,y∈Z ) )))_ ^ _() ^(•) )))

$$ \\ $$$$\:\:\:\:\:\:\:\begin{array}{|c|}{\overset{\bullet} {\:\:\:\:\:\begin{array}{|c|}{\:\:\:\underset{{x}=?,{y}=?\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} {\overset{{x},{y}\in\mathbb{Z}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} {{x}+{y}+{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{586}}}\:\:}\\\hline\end{array}_{} ^{} }\:\:\:\:}\\\hline\end{array} \\ $$$$ \\ $$

Question Number 161860 Answers: 1 Comments: 0

Simplify ((1^2 ∙2!+2^2 ∙3!+3^2 ∙4!+∙∙∙+n^2 (n+1)!−2)/((n+1)!)) to n^2 +n−2

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Simplify} \\ $$$$\frac{\mathrm{1}^{\mathrm{2}} \centerdot\mathrm{2}!+\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{3}!+\mathrm{3}^{\mathrm{2}} \centerdot\mathrm{4}!+\centerdot\centerdot\centerdot+{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)!−\mathrm{2}}{\left({n}+\mathrm{1}\right)!} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{to} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{n}^{\mathrm{2}} +\mathrm{n}−\mathrm{2} \\ $$

Question Number 161843 Answers: 0 Comments: 3

Q#161744 reposted with some change. Solve for integer numbers: (x/y) + (5/x) + ((y - 5)/5) = ((y + x)/(y + 5)) + ((5 + y)/(5 + x))

$${Q}#\mathrm{161744}\:{reposted}\:{with}\:{some}\:{change}. \\ $$$$\mathrm{Solve}\:\mathrm{for}\:\boldsymbol{\mathrm{integer}}\:\mathrm{numbers}: \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}\:+\:\frac{\mathrm{5}}{\mathrm{x}}\:+\:\frac{\mathrm{y}\:-\:\mathrm{5}}{\mathrm{5}}\:=\:\frac{\mathrm{y}\:+\:\mathrm{x}}{\mathrm{y}\:+\:\mathrm{5}}\:+\:\frac{\mathrm{5}\:+\:\mathrm{y}}{\mathrm{5}\:+\:\mathrm{x}} \\ $$

Question Number 161622 Answers: 1 Comments: 0

Σ_(n=1) ^∞ (((−1)^(n+1) )/(n(2n+1)))=?

$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}+\mathrm{1}} }{\boldsymbol{{n}}\left(\mathrm{2}\boldsymbol{{n}}+\mathrm{1}\right)}=? \\ $$

Question Number 161528 Answers: 1 Comments: 0

PROVE that the numbers of types 4k+2 & 4k+3 are NOT perfect □s.

$$\mathrm{PROVE}\:\mathrm{that}\:\mathrm{the}\:\mathrm{numbers}\:\mathrm{of}\:\mathrm{types} \\ $$$$\mathrm{4k}+\mathrm{2}\:\&\:\mathrm{4k}+\mathrm{3}\:\mathrm{are}\:\mathrm{NOT}\:\mathrm{perfect}\:\Box\mathrm{s}. \\ $$

Question Number 160270 Answers: 2 Comments: 0

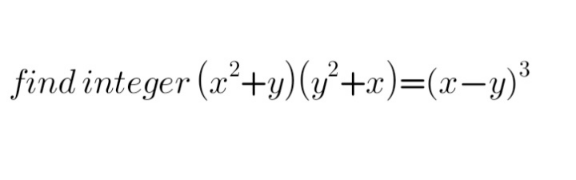
Question Number 160061 Answers: 1 Comments: 0

Find out some pairs (a,b) such that for some n≥1 a^n +b^n ,a^(2n) +b^(2n) ,a^(4n) +b^(4n) ,a^(8n) +b^(8n) ∈P

$$ \\ $$$${Find}\:{out}\:{some}\:{pairs}\:\left({a},{b}\right)\:{such}\:{that} \\ $$$${for}\:{some}\:{n}\geqslant\mathrm{1} \\ $$$${a}^{{n}} +{b}^{{n}} ,{a}^{\mathrm{2}{n}} +{b}^{\mathrm{2}{n}} ,{a}^{\mathrm{4}{n}} +{b}^{\mathrm{4}{n}} ,{a}^{\mathrm{8}{n}} +{b}^{\mathrm{8}{n}} \in\mathbb{P} \\ $$$$ \\ $$

Question Number 159925 Answers: 1 Comments: 0

Find out pairs of numbers (a,b) (as many as you can) such that: (√a) +(√b) , a+b , a^2 +b^2 ∈ P

$$\mathrm{Find}\:\mathrm{out}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{numbers}\:\left(\mathrm{a},\mathrm{b}\right)\:\left(\mathrm{as}\right. \\ $$$$\left.\mathrm{many}\:\mathrm{as}\:\mathrm{you}\:\mathrm{can}\right)\:\mathrm{such}\:\mathrm{that}: \\ $$$$\sqrt{\mathrm{a}}\:+\sqrt{\mathrm{b}}\:,\:\mathrm{a}+\mathrm{b}\:,\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \:\in\:\mathbb{P} \\ $$

Question Number 159775 Answers: 1 Comments: 0

Π_(n=1) ^∞ ((α^3 +β^2 )/3^n )= ? in expanded form

$$\prod_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\alpha^{\mathrm{3}} +\beta^{\mathrm{2}} }{\mathrm{3}^{\mathrm{n}} }=\:? \\ $$$$\mathrm{in}\:\mathrm{expanded}\:\mathrm{form} \\ $$

Pg 1 Pg 2 Pg 3 Pg 4 Pg 5 Pg 6 Pg 7 Pg 8 Pg 9 Pg 10

Contact: info@tinkutara.com