Question and Answers Forum

Number TheoryQuestion and Answers: Page 5

Question Number 182374 Answers: 2 Comments: 1

Question Number 181313 Answers: 2 Comments: 0

Montrer que 3^(2n+1) +2^(n+2) est divisible par 7

$${Montrer}\:{que} \\ $$$$\mathrm{3}^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{2}^{{n}+\mathrm{2}} \:\:\:{est}\:{divisible}\:{par}\:\mathrm{7} \\ $$

Question Number 180877 Answers: 1 Comments: 1

Q. find the largest value of such that the positive integers a, b > 1 satisfy. a^b .b^a + a^b + b^a = 5329

Question Number 180776 Answers: 2 Comments: 0

Simplify (√((4/( (√2))) + 3))

$${Simplify}\:\:\sqrt{\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}}}\:+\:\mathrm{3}}\: \\ $$$$ \\ $$

Question Number 180746 Answers: 2 Comments: 0

Question Number 180115 Answers: 1 Comments: 0

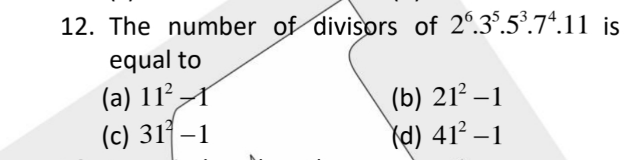
Question Number 178282 Answers: 2 Comments: 0

find unit digit of 1^1 +2^2 +3^3 +.......+63^(63) +64^(64)

$$ \\ $$$${find}\:{unit}\:{digit}\:{of}\: \\ $$$$\mathrm{1}^{\mathrm{1}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} +.......+\mathrm{63}^{\mathrm{63}} +\mathrm{64}^{\mathrm{64}} \\ $$

Question Number 178277 Answers: 0 Comments: 0

if 2^(pq) −2^(rs) =32; where p,q,r,s∈Z then possible values of p + q + r + s = ??

$$ \\ $$$${if}\:\mathrm{2}^{{pq}} −\mathrm{2}^{{rs}} =\mathrm{32};\:{where}\:{p},{q},{r},{s}\in\mathbb{Z}\: \\ $$$${then}\:{possible}\:{values}\:{of} \\ $$$${p}\:+\:{q}\:+\:{r}\:+\:{s}\:=\:?? \\ $$$$ \\ $$

Question Number 175799 Answers: 2 Comments: 0

For x ,y ε Z^+ such that 7x+9y=405. Find max value of x−y.

$$\:\:\mathrm{For}\:\mathrm{x}\:,\mathrm{y}\:\varepsilon\:\mathbb{Z}^{+} \:\mathrm{such}\:\mathrm{that}\: \\ $$$$\:\:\mathrm{7x}+\mathrm{9y}=\mathrm{405}.\:\mathrm{Find}\:\mathrm{max}\:\mathrm{value} \\ $$$$\:\:\mathrm{of}\:\mathrm{x}−\mathrm{y}. \\ $$

Question Number 175320 Answers: 3 Comments: 3

{ ((4x=2(mod 9))),((7x=2 (mod 13))) :}

$$\:\:\begin{cases}{\mathrm{4}{x}=\mathrm{2}\left({mod}\:\mathrm{9}\right)}\\{\mathrm{7}{x}=\mathrm{2}\:\left({mod}\:\mathrm{13}\right)}\end{cases} \\ $$

Question Number 175221 Answers: 2 Comments: 0

Question Number 174567 Answers: 0 Comments: 0

Question Number 174566 Answers: 1 Comments: 0

Question Number 172210 Answers: 2 Comments: 4

Solve in N: 6^x +6^y =222

$$\boldsymbol{\mathrm{Solve}}\:\boldsymbol{\mathrm{in}}\:\mathbb{N}: \\ $$$$\mathrm{6}^{\boldsymbol{\mathrm{x}}} +\mathrm{6}^{\boldsymbol{\mathrm{y}}} =\mathrm{222} \\ $$

Question Number 171431 Answers: 0 Comments: 0

Question Number 171359 Answers: 1 Comments: 0

A heavenly body has mass one third of the earth and its radius is half as that of the earth. if a stone weights 200N on the earth′s surface, find its weight on that heavenly body.

$$\mathrm{A}\:\mathrm{heavenly}\:\mathrm{body}\:\mathrm{has}\:\mathrm{mass}\:\mathrm{one}\:\mathrm{third}\:\mathrm{of}\:\mathrm{the}\:\mathrm{earth}\:\mathrm{and}\:\mathrm{its} \\ $$$$\:\mathrm{radius}\:\mathrm{is}\:\mathrm{half}\:\mathrm{as}\:\mathrm{that}\:\mathrm{of}\:\mathrm{the}\:\mathrm{earth}.\:\mathrm{if}\:\mathrm{a}\:\mathrm{stone}\:\mathrm{weights}\:\mathrm{200N}\:\mathrm{on} \\ $$$$\mathrm{the}\:\mathrm{earth}'\mathrm{s}\:\mathrm{surface},\:\mathrm{find}\:\mathrm{its}\:\mathrm{weight}\:\mathrm{on}\:\mathrm{that}\:\mathrm{heavenly}\:\mathrm{body}. \\ $$

Question Number 170772 Answers: 0 Comments: 0

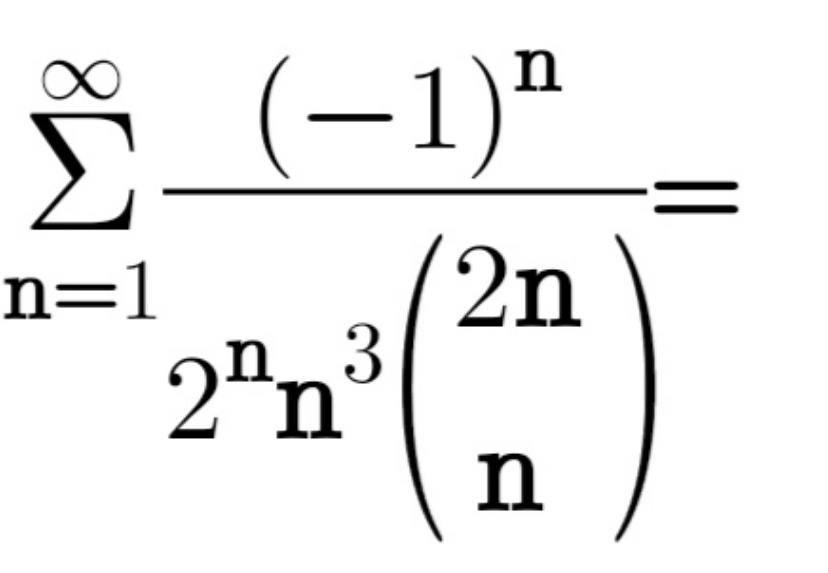
Question Number 170046 Answers: 2 Comments: 0

PROVE THAT 6 ∣ (8^x −2^x )

$$\mathrm{PROVE}\:\mathrm{THAT} \\ $$$$\:\:\:\:\mathrm{6}\:\mid\:\left(\mathrm{8}^{{x}} −\mathrm{2}^{{x}} \right) \\ $$

Question Number 170003 Answers: 1 Comments: 1

prove that Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 )=(π^2 /(12))

$${prove}\:{that} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$

Question Number 169982 Answers: 0 Comments: 0

$$ \\ $$

Question Number 169541 Answers: 1 Comments: 0

Question Number 168937 Answers: 1 Comments: 0

Determine m & n such that: digit-sum(m^2 )=n_(&_(digit-sum(n^2 )=m) ) ^■ digit-sum(abc..^(−) .)=a+b+c+...

$$ \\ $$$$\underline{\mathcal{D}{etermine}\:{m}\:\&\:{n}\:{such}\:{that}:} \\ $$$$\:\:\underset{\underset{{digit}-{sum}\left({n}^{\mathrm{2}} \right)={m}} {\&}} {\:{digit}-{sum}\left({m}^{\mathrm{2}} \right)={n}} \\ $$$$\:^{\blacksquare} {digit}-{sum}\left(\overline {{abc}..}.\right)={a}+{b}+{c}+...\:\:\:\:\:\:\:\: \\ $$

Question Number 168885 Answers: 0 Comments: 11

Find all the values of n such that: determinant (((digit-sum(n^3 )=n ))) and show that n has at most 2 digits. ^■ digit-sum(abc..^(−) )=a+b+c+...

$$ \\ $$$$\mathrm{Find}\:\mathrm{all}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{n}\:\mathrm{such}\:\mathrm{that}: \\ $$$$\:\:\:\:\begin{array}{|c|}{\mathrm{digit}-\mathrm{sum}\left(\mathrm{n}^{\mathrm{3}} \right)=\mathrm{n}\:}\\\hline\end{array} \\ $$$$\mathrm{and} \\ $$$$\mathrm{show}\:\mathrm{that}\:\mathrm{n}\:\mathrm{has}\:\mathrm{at}\:\mathrm{most}\:\mathrm{2}\:\mathrm{digits}. \\ $$$$\:\:^{\blacksquare} \mathrm{digit}-\mathrm{sum}\left(\overline {\mathrm{abc}..}\right)=\mathrm{a}+\mathrm{b}+\mathrm{c}+... \\ $$

Question Number 168823 Answers: 2 Comments: 0

Q#168480 reposted. n^2 +n+109=x^2 x∈Z, n(∈Z^+ )=?

$$\boldsymbol{\mathrm{Q}}#\mathrm{168480}\:\mathrm{reposted}. \\ $$$$\boldsymbol{\mathrm{n}}^{\mathrm{2}} +\boldsymbol{\mathrm{n}}+\mathrm{109}=\boldsymbol{\mathrm{x}}^{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{x}}\in\mathbb{Z},\:\boldsymbol{\mathrm{n}}\left(\in\mathbb{Z}^{+} \right)=? \\ $$

Question Number 168443 Answers: 0 Comments: 0

Question Number 168158 Answers: 0 Comments: 0

Pg 1 Pg 2 Pg 3 Pg 4 Pg 5 Pg 6 Pg 7 Pg 8 Pg 9 Pg 10

Contact: [email protected]