
Number TheoryQuestion and Answers: Page 14
Question Number 102467 Answers: 1 Comments: 5
Question Number 101888 Answers: 3 Comments: 1
Question Number 101418 Answers: 0 Comments: 6
Question Number 101043 Answers: 1 Comments: 0
Question Number 100888 Answers: 0 Comments: 0
Question Number 100733 Answers: 0 Comments: 6
Question Number 100677 Answers: 0 Comments: 0
Question Number 100583 Answers: 0 Comments: 0
Question Number 100179 Answers: 2 Comments: 0
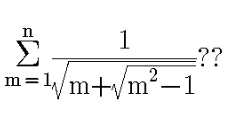
Question Number 100178 Answers: 2 Comments: 0
Question Number 100042 Answers: 1 Comments: 0
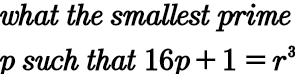
Question Number 99804 Answers: 0 Comments: 3
Question Number 99495 Answers: 2 Comments: 2
Question Number 99322 Answers: 1 Comments: 0
Question Number 98602 Answers: 2 Comments: 6
Question Number 98596 Answers: 1 Comments: 2

Question Number 98091 Answers: 1 Comments: 0
Question Number 97823 Answers: 4 Comments: 2
Question Number 97746 Answers: 1 Comments: 1
Question Number 97709 Answers: 0 Comments: 4

Question Number 97576 Answers: 2 Comments: 0
Question Number 97413 Answers: 1 Comments: 0
Question Number 96928 Answers: 3 Comments: 1
Question Number 96558 Answers: 1 Comments: 0
Question Number 96437 Answers: 1 Comments: 0

Question Number 95966 Answers: 1 Comments: 0
