
Question Number 104419 by Anindita last updated on 21/Jul/20

$$\boldsymbol{\mathrm{Now}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{sum}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{father}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{is}} \\ $$$$\mathrm{90}\:\boldsymbol{\mathrm{years}}.\:\mathrm{5}\:\boldsymbol{\mathrm{years}}\:\boldsymbol{\mathrm{ago}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{father}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{age}} \\ $$$$\boldsymbol{\mathrm{was}}\:\mathrm{3}\:\boldsymbol{\mathrm{times}}\:\boldsymbol{\mathrm{than}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{age}}.\:\boldsymbol{\mathrm{Write}}\:\boldsymbol{\mathrm{the}} \\ $$$$\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{age}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{father}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{age}}\:\mathrm{3}\:\boldsymbol{\mathrm{years}} \\ $$$$\boldsymbol{\mathrm{after}}. \\ $$
Answered by 1549442205PVT last updated on 22/Jul/20
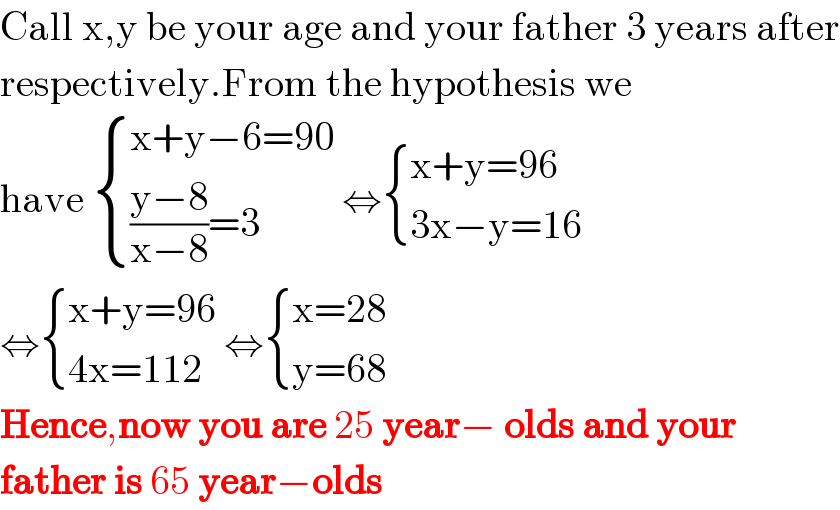
$$\mathrm{Call}\:\mathrm{x},\mathrm{y}\:\mathrm{be}\:\mathrm{your}\:\mathrm{age}\:\mathrm{and}\:\mathrm{your}\:\mathrm{father}\:\mathrm{3}\:\mathrm{years}\:\mathrm{after} \\ $$$$\mathrm{respectively}.\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{we} \\ $$$$\mathrm{have}\:\begin{cases}{\mathrm{x}+\mathrm{y}−\mathrm{6}=\mathrm{90}}\\{\frac{\mathrm{y}−\mathrm{8}}{\mathrm{x}−\mathrm{8}}=\mathrm{3}}\end{cases}\:\Leftrightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{96}}\\{\mathrm{3x}−\mathrm{y}=\mathrm{16}}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{96}}\\{\mathrm{4x}=\mathrm{112}}\end{cases}\:\Leftrightarrow\begin{cases}{\mathrm{x}=\mathrm{28}}\\{\mathrm{y}=\mathrm{68}}\end{cases} \\ $$$$\boldsymbol{\mathrm{Hence}},\boldsymbol{\mathrm{now}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{are}}\:\mathrm{25}\:\boldsymbol{\mathrm{year}}−\:\boldsymbol{\mathrm{olds}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{your}} \\ $$$$\boldsymbol{\mathrm{father}}\:\boldsymbol{\mathrm{is}}\:\mathrm{65}\:\boldsymbol{\mathrm{year}}−\boldsymbol{\mathrm{olds}} \\ $$
Commented by Rasheed.Sindhi last updated on 22/Jul/20

$$\mathrm{x}+\mathrm{y}\overset{???} {−\mathrm{6}}=\mathrm{90} \\ $$
Commented by 1549442205PVT last updated on 23/Jul/20
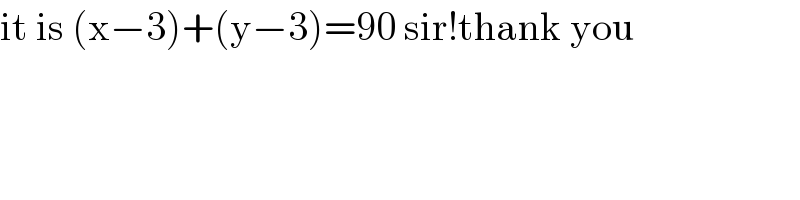
$$\mathrm{it}\:\mathrm{is}\:\left(\mathrm{x}−\mathrm{3}\right)+\left(\mathrm{y}−\mathrm{3}\right)=\mathrm{90}\:\mathrm{sir}!\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Rasheed.Sindhi last updated on 23/Jul/20

$$\:\:\:\mathrm{Using}\:\mathrm{one}\:\mathrm{variable} \\ $$$$\begin{vmatrix}{}&{{your}\:{age}}&{}&{{father}'{s}\:{age}}\\{−−−−}&{−−−−}&{−}&{−−−−−}\\{{Now}}&{\:\:\:\:\:\:\:{x}}&{}&{\:\:\:\:\:\:\mathrm{90}−{x}}\\{\mathrm{5}_{{years}} {ago}}&{\:\:\:\:{x}−\mathrm{5}}&{}&{\:\:\:\:\:\:\mathrm{85}−{x}}\\{−−−−}&{−−−−}&{−}&{−−−−−}\\{}&{\:\:\mathrm{3}\left({x}−\mathrm{5}\right)}&{=}&{\mathrm{85}−{x}}\\{\mathcal{E}{quation}}&{\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}{x}}&{=}&{\mathrm{85}+\mathrm{15}}\\{}&{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}}&{=}&{\mathrm{25}}\\{}&{\:\:\:\:\:\:\mathrm{90}−{x}}&{=}&{\mathrm{65}}\\{−−−−}&{−−−−}&{−}&{−−−−−}\\{{Result}}&{\:\:\:\:\:\:\:\:\:\mathrm{25}}&{}&{\:\:\:\:\:\:\:\:\mathrm{65}}\end{vmatrix}\:\:\: \\ $$$${After}\:\mathrm{3}\:{years}: \\ $$$${your}\:{age}=\mathrm{25}+\mathrm{3}=\mathrm{28}\:{years} \\ $$$${your}\:{father}'{s}\:{age}\:\mathrm{65}+\mathrm{3}=\mathrm{68} \\ $$$${years} \\ $$$$ \\ $$
