Question and Answers Forum

All Questions      Topic List

Probability and Statistics Questions

Previous in All Question      Next in All Question      

Previous in Probability and Statistics      Next in Probability and Statistics      

Question Number 131975 by liberty last updated on 10/Feb/21

Ninety students , including Joe and Jane are to be split into three classes of equal size and is to be done at random. What is the probability that Joe and Jane end up in the same class ?

$$\:\mathrm{Ninety}\:\mathrm{students}\:,\:\mathrm{including}\:\mathrm{Joe} \\ $$$$\mathrm{and}\:\mathrm{Jane}\:\mathrm{are}\:\mathrm{to}\:\mathrm{be}\:\mathrm{split}\:\mathrm{into}\: \\ $$$$\mathrm{three}\:\mathrm{classes}\:\mathrm{of}\:\mathrm{equal}\:\mathrm{size}\:\mathrm{and}\:\mathrm{is} \\ $$$$\mathrm{to}\:\mathrm{be}\:\mathrm{done}\:\mathrm{at}\:\mathrm{random}.\:\mathrm{What}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{Joe}\:\mathrm{and}\:\mathrm{Jane} \\ $$$$\mathrm{end}\:\mathrm{up}\:\mathrm{in}\:\mathrm{the}\:\mathrm{same}\:\mathrm{class}\:? \\ $$

Commented by liberty last updated on 10/Feb/21

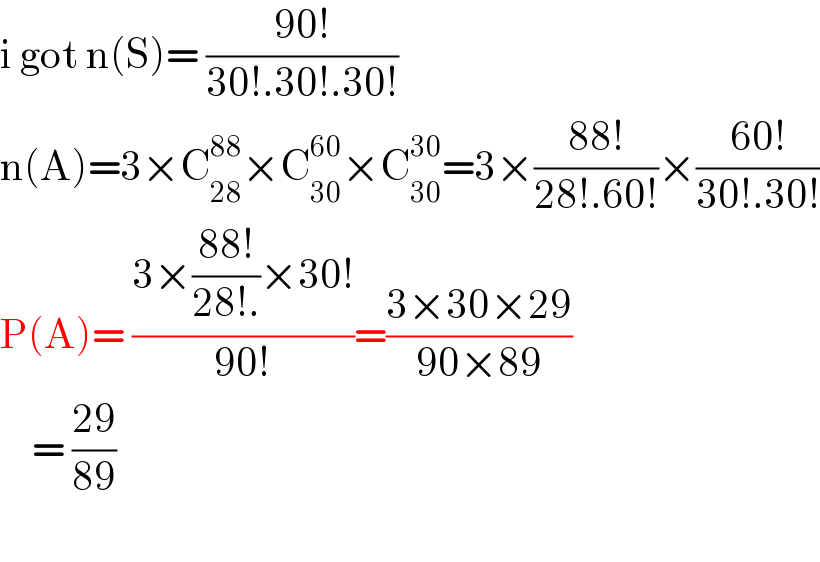
i got n(S)= ((90!)/(30!.30!.30!)) n(A)=3×C_(28) ^(88) ×C_(30) ^(60) ×C_(30) ^(30) =3×((88!)/(28!.60!))×((60!)/(30!.30!)) P(A)= ((3×((88!)/(28!.))×30!)/(90!))=((3×30×29)/(90×89)) = ((29)/(89))

$$\mathrm{i}\:\mathrm{got}\:\mathrm{n}\left(\mathrm{S}\right)=\:\frac{\mathrm{90}!}{\mathrm{30}!.\mathrm{30}!.\mathrm{30}!} \\ $$$$\mathrm{n}\left(\mathrm{A}\right)=\mathrm{3}×\mathrm{C}_{\mathrm{28}} ^{\mathrm{88}} ×\mathrm{C}_{\mathrm{30}} ^{\mathrm{60}} ×\mathrm{C}_{\mathrm{30}} ^{\mathrm{30}} =\mathrm{3}×\frac{\mathrm{88}!}{\mathrm{28}!.\mathrm{60}!}×\frac{\mathrm{60}!}{\mathrm{30}!.\mathrm{30}!} \\ $$$$\mathrm{P}\left(\mathrm{A}\right)=\:\frac{\mathrm{3}×\frac{\mathrm{88}!}{\mathrm{28}!.}×\mathrm{30}!}{\mathrm{90}!}=\frac{\mathrm{3}×\mathrm{30}×\mathrm{29}}{\mathrm{90}×\mathrm{89}} \\ $$$$\:\:\:\:=\:\frac{\mathrm{29}}{\mathrm{89}} \\ $$$$ \\ $$

Commented by liberty last updated on 10/Feb/21

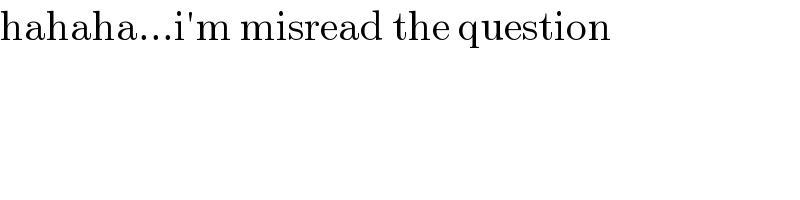
hahaha...i′m misread the question

$$\mathrm{hahaha}...\mathrm{i}'\mathrm{m}\:\mathrm{misread}\:\mathrm{the}\:\mathrm{question} \\ $$

Answered by TheSupreme last updated on 10/Feb/21

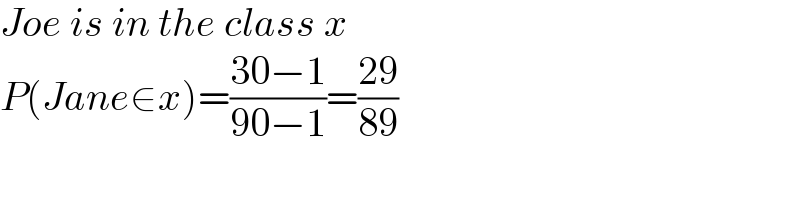
Joe is in the class x P(Jane∈x)=((30−1)/(90−1))=((29)/(89))

$${Joe}\:{is}\:{in}\:{the}\:{class}\:{x} \\ $$$${P}\left({Jane}\in{x}\right)=\frac{\mathrm{30}−\mathrm{1}}{\mathrm{90}−\mathrm{1}}=\frac{\mathrm{29}}{\mathrm{89}} \\ $$$$ \\ $$

Commented by liberty last updated on 10/Feb/21

haha its general formula

$$\mathrm{haha}\:\mathrm{its}\:\mathrm{general}\:\mathrm{formula} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com