
Question Number 131520 by EDWIN88 last updated on 05/Feb/21
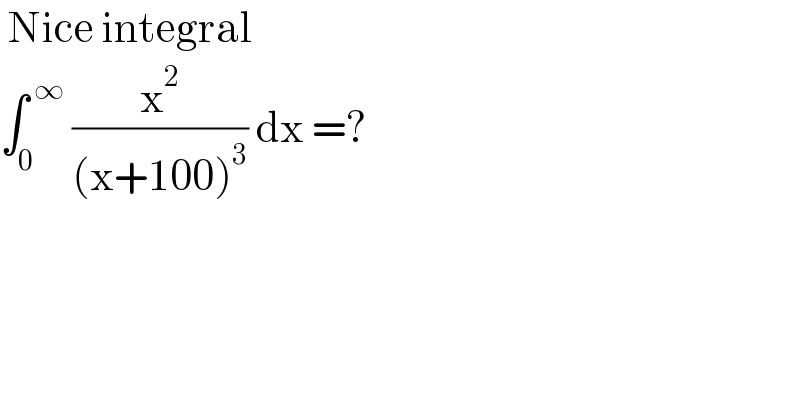
$$\:\mathrm{Nice}\:\mathrm{integral}\: \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}+\mathrm{100}\right)^{\mathrm{3}} }\:\mathrm{dx}\:=? \\ $$
Commented by liberty last updated on 05/Feb/21

$$\mathrm{diverges} \\ $$
Commented by Dwaipayan Shikari last updated on 05/Feb/21

$${I}\:{think}\:{it}\:{should}\:{be}\:\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{100}\right)^{\mathrm{3}} }{dx} \\ $$$${then} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\left({u}+\mathrm{100}\right)^{\mathrm{3}} }{du}\:\:\:\:\:{u}=\mathrm{100}{t} \\ $$$$=\frac{\mathrm{100}.\mathrm{10}}{\mathrm{2}.\mathrm{100}^{\mathrm{3}} }\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} }{\left({t}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}} }{dt}=\frac{\mathrm{1}}{\mathrm{2000}}.\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{3}\right)}=\frac{\pi}{\mathrm{16000}} \\ $$
