
Question Number 131673 by liberty last updated on 07/Feb/21
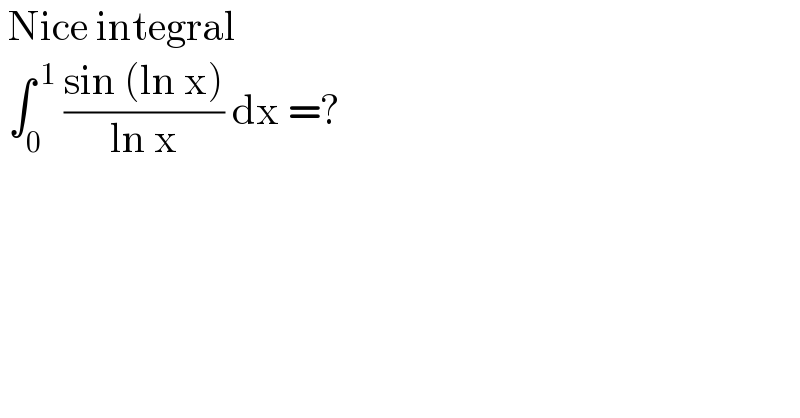
$$\:\mathrm{Nice}\:\mathrm{integral}\: \\ $$$$\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{sin}\:\left(\mathrm{ln}\:\mathrm{x}\right)}{\mathrm{ln}\:\mathrm{x}}\:\mathrm{dx}\:=? \\ $$
Answered by mindispower last updated on 07/Feb/21
![ln(x)=−t ⇒∫_0 ^∞ ((sin(t))/t)e^(−t) dt=A g(a)=∫_0 ^∞ ((sin(t)e^(−at) )/t)dt g′(a)=Im−∫_0 ^∞ e^((i−a)t) dt =−Im[(1/((a−i)))]=(1/(a^2 +1)) g(a)=tan^− (a)+c g(0)=(π/2)⇒g(a)=tan^− (a)+(π/2) A=g(1)=(π/4)+(π/2)=((3π)/4)](Q131675.png)
$${ln}\left({x}\right)=−{t} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({t}\right)}{{t}}{e}^{−{t}} {dt}={A} \\ $$$${g}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({t}\right){e}^{−{at}} }{{t}}{dt} \\ $$$${g}'\left({a}\right)={Im}−\int_{\mathrm{0}} ^{\infty} {e}^{\left({i}−{a}\right){t}} {dt} \\ $$$$=−{Im}\left[\frac{\mathrm{1}}{\left({a}−{i}\right)}\right]=\frac{\mathrm{1}}{{a}^{\mathrm{2}} +\mathrm{1}} \\ $$$${g}\left({a}\right)={tan}^{−} \left({a}\right)+{c} \\ $$$$\:{g}\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{2}}\Rightarrow{g}\left({a}\right)={tan}^{−} \left({a}\right)+\frac{\pi}{\mathrm{2}} \\ $$$${A}={g}\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{2}}=\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$
Commented by liberty last updated on 07/Feb/21

$$\mathrm{i}\:\mathrm{think}\:\mathrm{is}\:\frac{\pi}{\mathrm{4}}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 07/Feb/21

$$\mathrm{sir}\:\mathrm{small}\:\mathrm{error}\:\:−\mathrm{Im}\left(\frac{\mathrm{1}}{\mathrm{a}−\mathrm{i}}\right)=−\mathrm{Im}\left(\frac{\mathrm{a}+\mathrm{i}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\right)=−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:\Rightarrow.... \\ $$
Answered by Dwaipayan Shikari last updated on 07/Feb/21
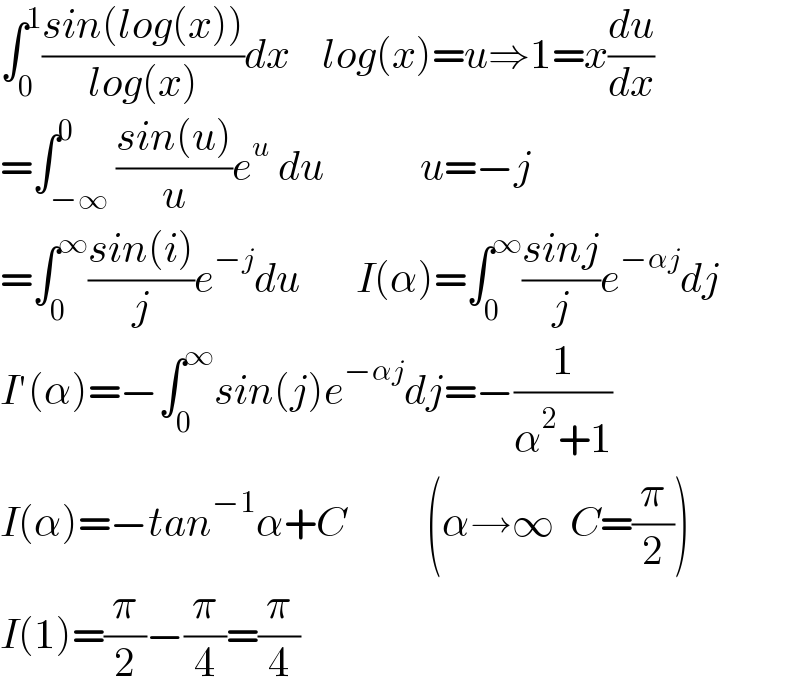
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sin}\left({log}\left({x}\right)\right)}{{log}\left({x}\right)}{dx}\:\:\:\:{log}\left({x}\right)={u}\Rightarrow\mathrm{1}={x}\frac{{du}}{{dx}} \\ $$$$=\int_{−\infty} ^{\mathrm{0}} \frac{{sin}\left({u}\right)}{{u}}{e}^{{u}} \:{du}\:\:\:\:\:\:\:\:\:\:\:\:{u}=−{j} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({i}\right)}{{j}}{e}^{−{j}} {du}\:\:\:\:\:\:\:{I}\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{sinj}}{{j}}{e}^{−\alpha{j}} {dj} \\ $$$${I}'\left(\alpha\right)=−\int_{\mathrm{0}} ^{\infty} {sin}\left({j}\right){e}^{−\alpha{j}} {dj}=−\frac{\mathrm{1}}{\alpha^{\mathrm{2}} +\mathrm{1}} \\ $$$${I}\left(\alpha\right)=−{tan}^{−\mathrm{1}} \alpha+{C}\:\:\:\:\:\:\:\:\:\:\left(\alpha\rightarrow\infty\:\:{C}=\frac{\pi}{\mathrm{2}}\right) \\ $$$${I}\left(\mathrm{1}\right)=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{4}} \\ $$
Commented by liberty last updated on 07/Feb/21

$$\mathrm{okay} \\ $$
Answered by liberty last updated on 07/Feb/21

$$\mathrm{I}\left(\beta\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{sin}\:\left(\beta\:\mathrm{ln}\:\mathrm{x}\right)}{\mathrm{ln}\:\mathrm{x}}\:\mathrm{dx}\: \\ $$$$\mathrm{I}\:'\left(\beta\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\:\left(\mathrm{x}\right)\:\frac{\mathrm{cos}\:\left(\beta\:\mathrm{ln}\:\mathrm{x}\right)}{\mathrm{ln}\:\left(\mathrm{x}\right)}\:\mathrm{dx}\: \\ $$$$\mathrm{I}\:'\left(\beta\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{cos}\:\left(\beta\:\mathrm{ln}\:\mathrm{x}\right)\:\mathrm{dx}\: \\ $$$$\mathrm{change}\:\mathrm{of}\:\mathrm{variables}\:\mathrm{u}\:=\:\mathrm{ln}\:\left(\mathrm{x}\right) \\ $$$$\mathrm{I}\:'\left(\beta\right)=\underset{−\infty} {\overset{\mathrm{0}} {\int}}\mathrm{cos}\:\left(\beta\mathrm{u}\right)\:\mathrm{e}^{\mathrm{u}} \:\mathrm{du}\: \\ $$$$\mathrm{I}\:'\left(\beta\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+\beta^{\mathrm{2}} }\:\mathrm{then}\:\mathrm{I}\left(\beta\right)\:=\:\mathrm{arctan}\:\left(\beta\right)\:+\mathrm{C} \\ $$$$\mathrm{setting}\:\beta\:=\:\mathrm{0}\:\mathrm{hence}\:\mathrm{C}\:=\:\mathrm{0} \\ $$$$\mathrm{I}\left(\beta=\mathrm{1}\right)=\:\mathrm{arctan}\:\mathrm{1}\:=\:\frac{\pi}{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 07/Feb/21
![Φ =∫_0 ^1 ((sin(lnx))/(lnx))dx we do the changement lnx=−t ⇒x=e^(−t) Φ =−∫_0 ^∞ ((sin(−t))/(−t))(−e^(−t) )dt =∫_0 ^∞ ((sint)/t)e^(−t) dt let consider f(a) =∫_0 ^∞ ((sint)/t)e^(−at) with a>0 ⇒f^′ (a) =−∫_0 ^∞ sint e^(−at) dt =−Im(∫_0 ^∞ e^(it−at) dt) we have ∫_0 ^∞ e^((−a+i)t) dt =[(1/(−a+i))e^((−a+i)t) ]_0 ^∞ =−(1/(a−i))(−1) =(1/(a−i))=((a+i)/(a^2 +1)) ⇒f^′ (a)=−(1/(1+a^2 )) ⇒f(a)=c−arctan(a) f(0)=c=∫_0 ^∞ ((sint)/t)dt =(π/2) ⇒f(a)=(π/2)−arctan(a) Φ =f(1) =(π/2)−arctan(1) =(π/2)−(π/4) =(π/4)](Q131740.png)
$$\Phi\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{sin}\left(\mathrm{lnx}\right)}{\mathrm{lnx}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{lnx}=−\mathrm{t}\:\Rightarrow\mathrm{x}=\mathrm{e}^{−\mathrm{t}} \\ $$$$\Phi\:=−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sin}\left(−\mathrm{t}\right)}{−\mathrm{t}}\left(−\mathrm{e}^{−\mathrm{t}} \right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sint}}{\mathrm{t}}\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:\mathrm{let}\:\mathrm{consider} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sint}}{\mathrm{t}}\mathrm{e}^{−\mathrm{at}} \:\:\:\mathrm{with}\:\mathrm{a}>\mathrm{0}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\mathrm{sint}\:\mathrm{e}^{−\mathrm{at}} \:\mathrm{dt} \\ $$$$=−\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\mathrm{it}−\mathrm{at}} \:\mathrm{dt}\right)\:\:\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\mathrm{a}+\mathrm{i}\right)\mathrm{t}} \mathrm{dt}\:=\left[\frac{\mathrm{1}}{−\mathrm{a}+\mathrm{i}}\mathrm{e}^{\left(−\mathrm{a}+\mathrm{i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{a}−\mathrm{i}}\left(−\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{a}−\mathrm{i}}=\frac{\mathrm{a}+\mathrm{i}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)=\mathrm{c}−\mathrm{arctan}\left(\mathrm{a}\right) \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=\mathrm{c}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{sint}}{\mathrm{t}}\mathrm{dt}\:=\frac{\pi}{\mathrm{2}}\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)=\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{a}\right) \\ $$$$\Phi\:=\mathrm{f}\left(\mathrm{1}\right)\:=\frac{\pi}{\mathrm{2}}−\mathrm{arctan}\left(\mathrm{1}\right)\:=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\:=\frac{\pi}{\mathrm{4}} \\ $$
