
Question Number 124109 by mathocean1 last updated on 30/Nov/20

$$ \\ $$$$ \\ $$$${N}={x}\mathrm{32}{y}\:{in}\:{base}\:\mathrm{5}. \\ $$$${determinate}\:{x}\:{and}\:{y}\:{such}\:{that}\:{N}\:{is} \\ $$$${divisible}\:{by}\:\mathrm{3}\:{and}\:\mathrm{4}. \\ $$
Answered by floor(10²Eta[1]) last updated on 03/Dec/20
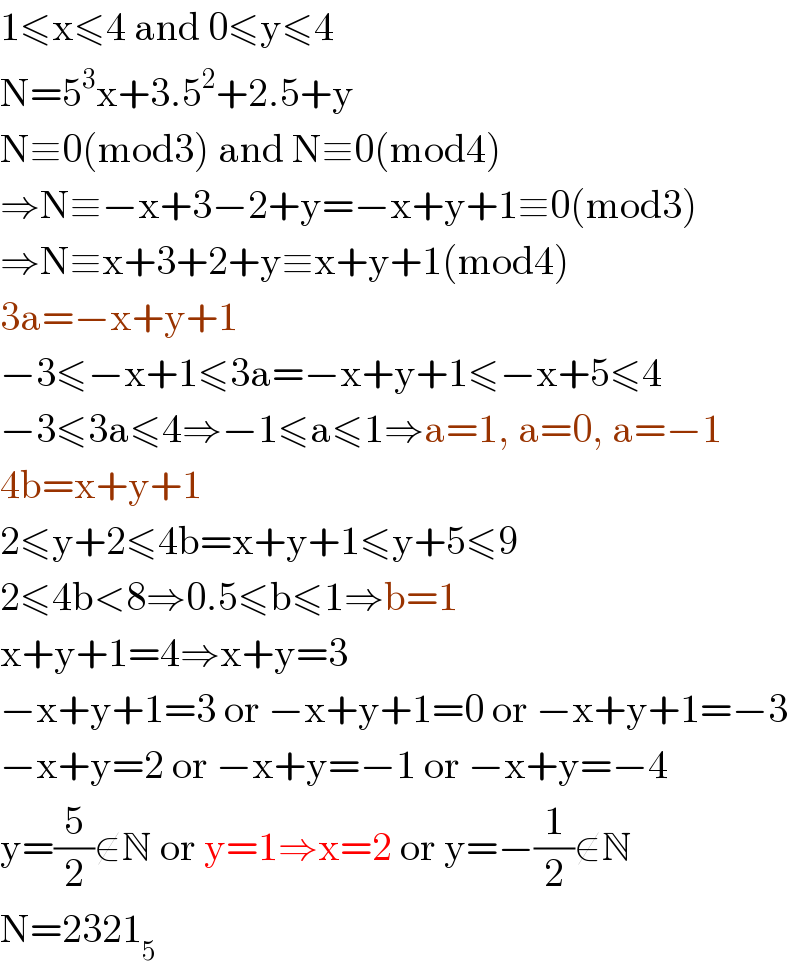
$$\mathrm{1}\leqslant\mathrm{x}\leqslant\mathrm{4}\:\mathrm{and}\:\mathrm{0}\leqslant\mathrm{y}\leqslant\mathrm{4} \\ $$$$\mathrm{N}=\mathrm{5}^{\mathrm{3}} \mathrm{x}+\mathrm{3}.\mathrm{5}^{\mathrm{2}} +\mathrm{2}.\mathrm{5}+\mathrm{y} \\ $$$$\mathrm{N}\equiv\mathrm{0}\left(\mathrm{mod3}\right)\:\mathrm{and}\:\mathrm{N}\equiv\mathrm{0}\left(\mathrm{mod4}\right) \\ $$$$\Rightarrow\mathrm{N}\equiv−\mathrm{x}+\mathrm{3}−\mathrm{2}+\mathrm{y}=−\mathrm{x}+\mathrm{y}+\mathrm{1}\equiv\mathrm{0}\left(\mathrm{mod3}\right) \\ $$$$\Rightarrow\mathrm{N}\equiv\mathrm{x}+\mathrm{3}+\mathrm{2}+\mathrm{y}\equiv\mathrm{x}+\mathrm{y}+\mathrm{1}\left(\mathrm{mod4}\right) \\ $$$$\mathrm{3a}=−\mathrm{x}+\mathrm{y}+\mathrm{1} \\ $$$$−\mathrm{3}\leqslant−\mathrm{x}+\mathrm{1}\leqslant\mathrm{3a}=−\mathrm{x}+\mathrm{y}+\mathrm{1}\leqslant−\mathrm{x}+\mathrm{5}\leqslant\mathrm{4} \\ $$$$−\mathrm{3}\leqslant\mathrm{3a}\leqslant\mathrm{4}\Rightarrow−\mathrm{1}\leqslant\mathrm{a}\leqslant\mathrm{1}\Rightarrow\mathrm{a}=\mathrm{1},\:\mathrm{a}=\mathrm{0},\:\mathrm{a}=−\mathrm{1} \\ $$$$\mathrm{4b}=\mathrm{x}+\mathrm{y}+\mathrm{1} \\ $$$$\mathrm{2}\leqslant\mathrm{y}+\mathrm{2}\leqslant\mathrm{4b}=\mathrm{x}+\mathrm{y}+\mathrm{1}\leqslant\mathrm{y}+\mathrm{5}\leqslant\mathrm{9} \\ $$$$\mathrm{2}\leqslant\mathrm{4b}<\mathrm{8}\Rightarrow\mathrm{0}.\mathrm{5}\leqslant\mathrm{b}\leqslant\mathrm{1}\Rightarrow\mathrm{b}=\mathrm{1} \\ $$$$\mathrm{x}+\mathrm{y}+\mathrm{1}=\mathrm{4}\Rightarrow\mathrm{x}+\mathrm{y}=\mathrm{3} \\ $$$$−\mathrm{x}+\mathrm{y}+\mathrm{1}=\mathrm{3}\:\mathrm{or}\:−\mathrm{x}+\mathrm{y}+\mathrm{1}=\mathrm{0}\:\mathrm{or}\:−\mathrm{x}+\mathrm{y}+\mathrm{1}=−\mathrm{3}\: \\ $$$$−\mathrm{x}+\mathrm{y}=\mathrm{2}\:\mathrm{or}\:−\mathrm{x}+\mathrm{y}=−\mathrm{1}\:\mathrm{or}\:−\mathrm{x}+\mathrm{y}=−\mathrm{4} \\ $$$$\mathrm{y}=\frac{\mathrm{5}}{\mathrm{2}}\notin\mathbb{N}\:\mathrm{or}\:\mathrm{y}=\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{2}\:\mathrm{or}\:\mathrm{y}=−\frac{\mathrm{1}}{\mathrm{2}}\notin\mathbb{N} \\ $$$$\mathrm{N}=\mathrm{2321}_{\mathrm{5}} \\ $$
Commented by floor(10²Eta[1]) last updated on 03/Dec/20
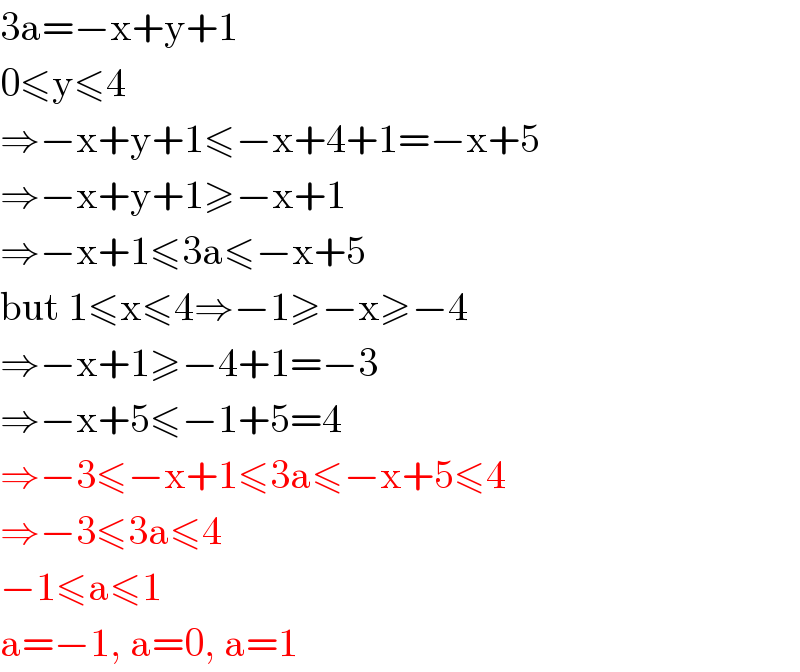
$$\mathrm{3a}=−\mathrm{x}+\mathrm{y}+\mathrm{1} \\ $$$$\mathrm{0}\leqslant\mathrm{y}\leqslant\mathrm{4} \\ $$$$\Rightarrow−\mathrm{x}+\mathrm{y}+\mathrm{1}\leqslant−\mathrm{x}+\mathrm{4}+\mathrm{1}=−\mathrm{x}+\mathrm{5} \\ $$$$\Rightarrow−\mathrm{x}+\mathrm{y}+\mathrm{1}\geqslant−\mathrm{x}+\mathrm{1} \\ $$$$\Rightarrow−\mathrm{x}+\mathrm{1}\leqslant\mathrm{3a}\leqslant−\mathrm{x}+\mathrm{5} \\ $$$$\mathrm{but}\:\mathrm{1}\leqslant\mathrm{x}\leqslant\mathrm{4}\Rightarrow−\mathrm{1}\geqslant−\mathrm{x}\geqslant−\mathrm{4} \\ $$$$\Rightarrow−\mathrm{x}+\mathrm{1}\geqslant−\mathrm{4}+\mathrm{1}=−\mathrm{3} \\ $$$$\Rightarrow−\mathrm{x}+\mathrm{5}\leqslant−\mathrm{1}+\mathrm{5}=\mathrm{4} \\ $$$$\Rightarrow−\mathrm{3}\leqslant−\mathrm{x}+\mathrm{1}\leqslant\mathrm{3a}\leqslant−\mathrm{x}+\mathrm{5}\leqslant\mathrm{4} \\ $$$$\Rightarrow−\mathrm{3}\leqslant\mathrm{3a}\leqslant\mathrm{4} \\ $$$$−\mathrm{1}\leqslant\mathrm{a}\leqslant\mathrm{1} \\ $$$$\mathrm{a}=−\mathrm{1},\:\mathrm{a}=\mathrm{0},\:\mathrm{a}=\mathrm{1} \\ $$
Commented by mathocean1 last updated on 03/Dec/20
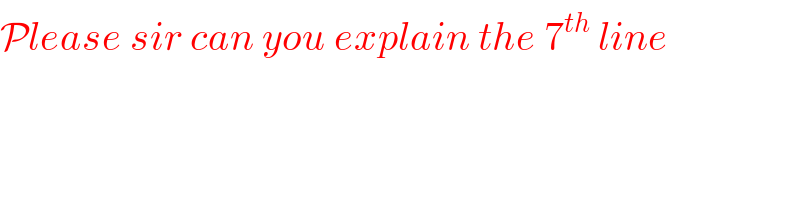
$$\mathcal{P}{lease}\:{sir}\:{can}\:{you}\:{explain}\:{the}\:\mathrm{7}^{{th}} \:{line} \\ $$
Commented by mathocean1 last updated on 03/Dec/20
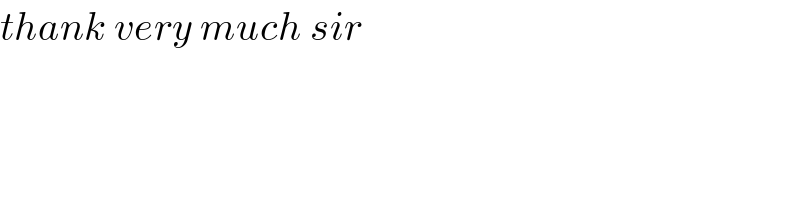
$${thank}\:{very}\:{much}\:{sir} \\ $$
