
Question Number 124110 by mathocean1 last updated on 30/Nov/20
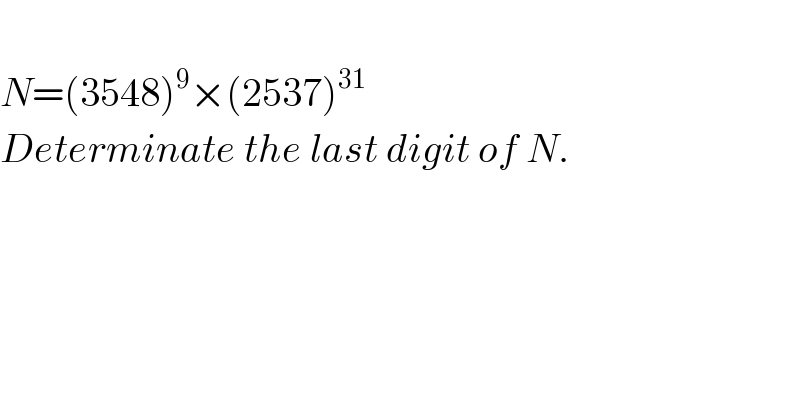
$$ \\ $$$${N}=\left(\mathrm{3548}\right)^{\mathrm{9}} ×\left(\mathrm{2537}\right)^{\mathrm{31}} \\ $$$${Determinate}\:{the}\:{last}\:{digit}\:{of}\:{N}. \\ $$
Answered by floor(10²Eta[1]) last updated on 24/Dec/20
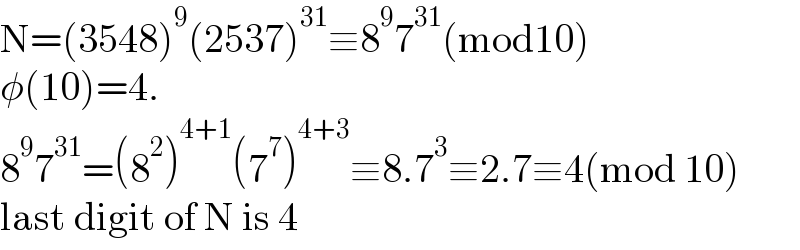
$$\mathrm{N}=\left(\mathrm{3548}\right)^{\mathrm{9}} \left(\mathrm{2537}\right)^{\mathrm{31}} \equiv\mathrm{8}^{\mathrm{9}} \mathrm{7}^{\mathrm{31}} \left(\mathrm{mod10}\right) \\ $$$$\phi\left(\mathrm{10}\right)=\mathrm{4}. \\ $$$$\mathrm{8}^{\mathrm{9}} \mathrm{7}^{\mathrm{31}} =\left(\mathrm{8}^{\mathrm{2}} \right)^{\mathrm{4}+\mathrm{1}} \left(\mathrm{7}^{\mathrm{7}} \right)^{\mathrm{4}+\mathrm{3}} \equiv\mathrm{8}.\mathrm{7}^{\mathrm{3}} \equiv\mathrm{2}.\mathrm{7}\equiv\mathrm{4}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{N}\:\mathrm{is}\:\mathrm{4} \\ $$
Answered by MJS_new last updated on 30/Nov/20
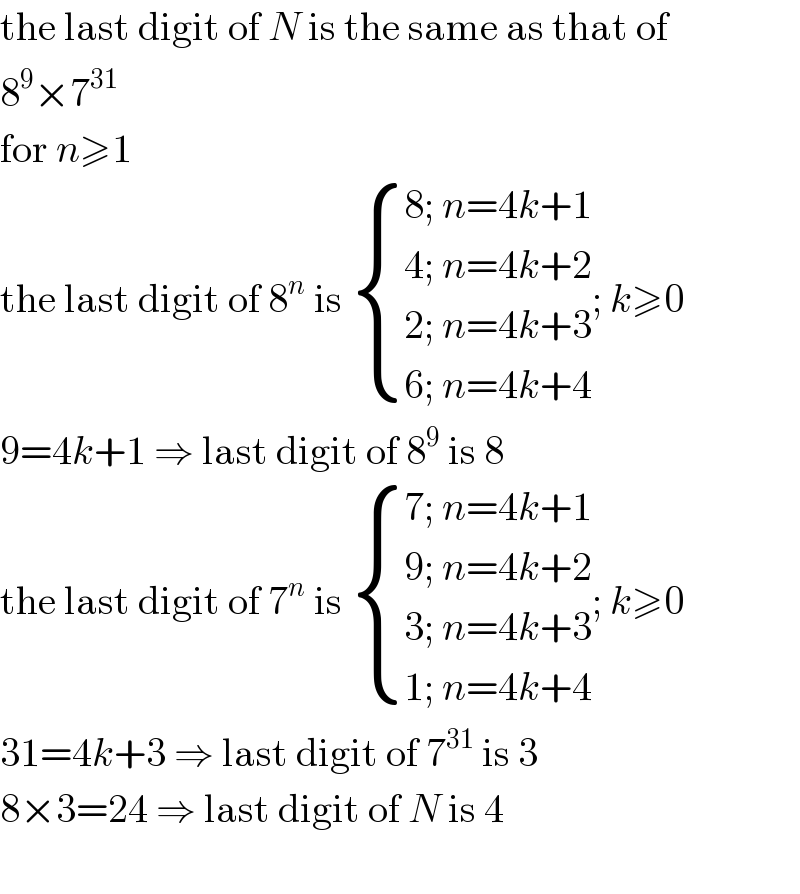
$$\mathrm{the}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:{N}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{that}\:\mathrm{of} \\ $$$$\mathrm{8}^{\mathrm{9}} ×\mathrm{7}^{\mathrm{31}} \\ $$$$\mathrm{for}\:{n}\geqslant\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{8}^{{n}} \:\mathrm{is}\:\begin{cases}{\mathrm{8};\:{n}=\mathrm{4}{k}+\mathrm{1}}\\{\mathrm{4};\:{n}=\mathrm{4}{k}+\mathrm{2}}\\{\mathrm{2};\:{n}=\mathrm{4}{k}+\mathrm{3}}\\{\mathrm{6};\:{n}=\mathrm{4}{k}+\mathrm{4}}\end{cases};\:{k}\geqslant\mathrm{0} \\ $$$$\mathrm{9}=\mathrm{4}{k}+\mathrm{1}\:\Rightarrow\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{8}^{\mathrm{9}} \:\mathrm{is}\:\mathrm{8} \\ $$$$\mathrm{the}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{7}^{{n}} \:\mathrm{is}\:\begin{cases}{\mathrm{7};\:{n}=\mathrm{4}{k}+\mathrm{1}}\\{\mathrm{9};\:{n}=\mathrm{4}{k}+\mathrm{2}}\\{\mathrm{3};\:{n}=\mathrm{4}{k}+\mathrm{3}}\\{\mathrm{1};\:{n}=\mathrm{4}{k}+\mathrm{4}}\end{cases};\:{k}\geqslant\mathrm{0} \\ $$$$\mathrm{31}=\mathrm{4}{k}+\mathrm{3}\:\Rightarrow\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{7}^{\mathrm{31}} \:\mathrm{is}\:\mathrm{3} \\ $$$$\mathrm{8}×\mathrm{3}=\mathrm{24}\:\Rightarrow\:\mathrm{last}\:\mathrm{digit}\:\mathrm{of}\:{N}\:\mathrm{is}\:\mathrm{4} \\ $$$$ \\ $$
