
Question Number 13031 by FilupS last updated on 12/May/17

$$\mathrm{MrW1} \\ $$$$ \\ $$$$\mathrm{Going}\:\mathrm{off}\:\mathrm{of}\:\mathrm{Q12883} \\ $$$$\: \\ $$$$\mathrm{How}\:\mathrm{many}\:\mathrm{unique}\:\mathrm{angles}\:\mathrm{angles}\:\mathrm{in}\:\mathbb{Z}^{\mathrm{3}} ? \\ $$$$\mathrm{What}\:\mathrm{about}\:\mathbb{Z}^{{n}} ? \\ $$
Answered by mrW1 last updated on 12/May/17
![For 1≤x_i ≤p_i with 1≤i≤n and x_i ∈P^n the number of unique angles for points P(x_(1,) x_2 ,∙∙∙,x_i ,∙∙∙,x_n ) is Φ=Π_(i=1) ^n p_i −Σ_(x_1 =1) ^p_1 Σ_(x_2 =1) ^p_2 ∙∙∙Σ_(x_i =1) ^p_i ∙∙∙Σ_(x_n =1) ^p_n sign[GCD(x_1 ,x_2 ,∙∙∙,x_i ,∙∙∙,x_n )−1]](Q13032.png)
$${For}\:\mathrm{1}\leqslant{x}_{{i}} \leqslant{p}_{{i}} \:{with}\:\mathrm{1}\leqslant{i}\leqslant{n}\:{and}\:{x}_{{i}} \:\in\mathbb{P}^{{n}} \\ $$$${the}\:{number}\:{of}\:{unique}\:{angles}\:{for}\:{points}\: \\ $$$${P}\left({x}_{\mathrm{1},} {x}_{\mathrm{2}} ,\centerdot\centerdot\centerdot,{x}_{{i}} ,\centerdot\centerdot\centerdot,{x}_{{n}} \right)\:{is} \\ $$$$\Phi=\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{i}} −\underset{{x}_{\mathrm{1}} =\mathrm{1}} {\overset{{p}_{\mathrm{1}} } {\sum}}\underset{{x}_{\mathrm{2}} =\mathrm{1}} {\overset{{p}_{\mathrm{2}} } {\sum}}\centerdot\centerdot\centerdot\underset{{x}_{{i}} =\mathrm{1}} {\overset{{p}_{{i}} } {\sum}}\centerdot\centerdot\centerdot\underset{{x}_{{n}} =\mathrm{1}} {\overset{{p}_{{n}} } {\sum}}{sign}\left[{GCD}\left({x}_{\mathrm{1}} ,{x}_{\mathrm{2}} ,\centerdot\centerdot\centerdot,{x}_{{i}} ,\centerdot\centerdot\centerdot,{x}_{{n}} \right)−\mathrm{1}\right] \\ $$
Commented by mrW1 last updated on 12/May/17
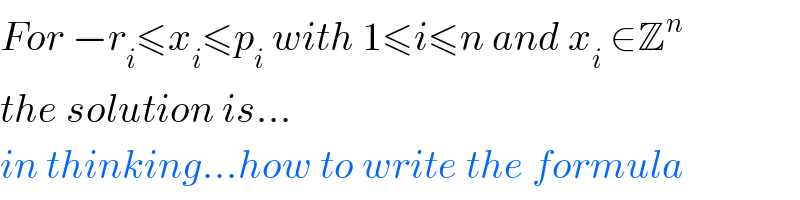
$${For}\:−{r}_{{i}} \leqslant{x}_{{i}} \leqslant{p}_{{i}} \:{with}\:\mathrm{1}\leqslant{i}\leqslant{n}\:{and}\:{x}_{{i}} \:\in\mathbb{Z}^{{n}} \\ $$$${the}\:{solution}\:{is}... \\ $$$${in}\:{thinking}...{how}\:{to}\:{write}\:{the}\:{formula} \\ $$
Commented by FilupS last updated on 12/May/17

$$\mathrm{why}\:\mathrm{is}\:{x}_{{i}} \in\mathbb{P}^{{n}} ? \\ $$
Commented by mrW1 last updated on 12/May/17

$${I}\:{wanted}\:{to}\:{solve}\:{this}\:{simple}\:{case}\:{at} \\ $$$${first}:\:\mathrm{1}\leqslant{x}_{{i}} \leqslant{p}_{{i}} . \\ $$$${The}\:{result}\:{for}\:{the}\:{case}\:−{r}_{{i}} \leqslant{x}_{{i}} \leqslant−\mathrm{1}\:{is} \\ $$$${the}\:{same}\:{as}\:\:{for}\:\mathrm{1}\leqslant{x}_{{i}} \leqslant{r}_{{i}} . \\ $$$${It}\:{means}\:{the}\:{problem}\:{for}\:{x}_{{i}} \in\mathbb{Z}^{{n}} \:{will} \\ $$$${be}\:{solved}\:{as}\:{a}\:{couple}\:{of}\:{problems} \\ $$$${for}\:{x}_{{i}} \in\mathbb{P}^{{n}.} \\ $$
Commented by mrW1 last updated on 12/May/17

$${Example}:\:{the}\:{solution}\:{for} \\ $$$$−\mathrm{127}\leqslant{x}\leqslant\mathrm{128} \\ $$$$−\mathrm{128}\leqslant{y}\leqslant\mathrm{127} \\ $$$${is}: \\ $$$$\Phi=\mathrm{128}×\mathrm{127}−\underset{{i}=\mathrm{1}} {\overset{\mathrm{128}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{\mathrm{127}} {\sum}}{sign}\left({GCD}\left({i},{j}\right)−\mathrm{1}\right) \\ $$$$+\mathrm{127}×\mathrm{127}−\underset{{i}=\mathrm{1}} {\overset{\mathrm{127}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{\mathrm{127}} {\sum}}{sign}\left({GCD}\left({i},{j}\right)−\mathrm{1}\right) \\ $$$$+\mathrm{127}×\mathrm{128}−\underset{{i}=\mathrm{1}} {\overset{\mathrm{127}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{\mathrm{128}} {\sum}}{sign}\left({GCD}\left({i},{j}\right)−\mathrm{1}\right) \\ $$$$+\mathrm{128}×\mathrm{128}−\underset{{i}=\mathrm{1}} {\overset{\mathrm{128}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{\mathrm{128}} {\sum}}{sign}\left({GCD}\left({i},{j}\right)−\mathrm{1}\right) \\ $$$$+\mathrm{4} \\ $$$$ \\ $$$${with}\:{line}\:\mathrm{1}\:{for}\:{quadrant}\:\mathrm{1}\:{and} \\ $$$${line}\:\mathrm{2}\:{for}\:{quadrant}\:\mathrm{2}\:{and} \\ $$$${line}\:\mathrm{3}\:{for}\:{quadrant}\:\mathrm{3}\:{and} \\ $$$${line}\:\mathrm{4}\:{for}\:{quadrant}\:\mathrm{4}\:{and} \\ $$$${line}\:\mathrm{5}\:{for}\:{points}\:{on}\:{axes} \\ $$
Commented by FilupS last updated on 12/May/17
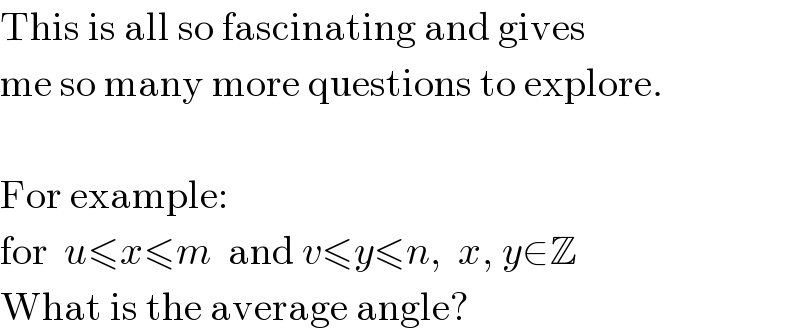
$$\mathrm{This}\:\mathrm{is}\:\mathrm{all}\:\mathrm{so}\:\mathrm{fascinating}\:\mathrm{and}\:\mathrm{gives} \\ $$$$\mathrm{me}\:\mathrm{so}\:\mathrm{many}\:\mathrm{more}\:\mathrm{questions}\:\mathrm{to}\:\mathrm{explore}. \\ $$$$\: \\ $$$$\mathrm{For}\:\mathrm{example}: \\ $$$$\mathrm{for}\:\:{u}\leqslant{x}\leqslant{m}\:\:\mathrm{and}\:{v}\leqslant{y}\leqslant{n},\:\:{x},\:{y}\in\mathbb{Z} \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{average}\:\mathrm{angle}? \\ $$
Commented by mrW1 last updated on 12/May/17
![Let′s say −u≤x≤m and −v≤y≤n. In quadrant 1 we have θ_(ij) =tan^(−1) ((y/x))=tan^(−1) ((j/i))=tan^(−1) (((j′)/(i′))) S_1 =Σ_(i=1) ^m Σ_(j=1) ^n θ_(ij) =Σ_(i=1) ^m Σ_(j=1) ^n tan^(−1) ((j/i)) In quadrant 2 we have θ_(ij) =tan^(−1) ((y/x))=π−tan^(−1) ((j/i))=π−tan^(−1) (((j′)/(i′))) S_2 =Σ_(i=1) ^u Σ_(j=1) ^n θ_(ij) =unπ−Σ_(i=1) ^u Σ_(j=1) ^n tan^(−1) ((j/i)) In quadrant 3 we have θ_(ij) =tan^(−1) ((y/x))=π+tan^(−1) ((j/i))=π+tan^(−1) (((j′)/(i′))) S_3 =Σ_(i=1) ^u Σ_(j=1) ^v θ_(ij) =uvπ+Σ_(i=1) ^u Σ_(j=1) ^v tan^(−1) ((j/i)) In quadrant 4 we have θ_(ij) =tan^(−1) ((y/x))=2π−tan^(−1) ((j/i))=2π−tan^(−1) (((j′)/(i′))) S_4 =Σ_(i=1) ^m Σ_(j=1) ^v θ_(ij) =2mvπ−Σ_(i=1) ^m Σ_(j=1) ^v tan^(−1) ((j/i)) On +x axis: m points with angle 0, On +y axis: n points with angle (π/2), On −x axis: u points with angle π, On −y axis: v points with angle ((3π)/2), S_5 =m×0+n×(π/2)+uπ+v×((3π)/2)=(((n+2u+3v)π)/2) Sum of all angles: S=S_1 +S_2 +S_3 +S_4 +S_5 =Σ_(i=1) ^m Σ_(j=1) ^n tan^(−1) ((j/i)) +unπ−Σ_(i=1) ^u Σ_(j=1) ^n tan^(−1) ((j/i)) +uvπ+Σ_(i=1) ^u Σ_(j=1) ^v tan^(−1) ((j/i)) +2mvπ−Σ_(i=1) ^m Σ_(j=1) ^v tan^(−1) ((j/i)) +(((n+2u+3v)π)/2) =(((2un+2uv+4mv+n+2u+3v)π)/2) +[Σ_(i=1) ^m −Σ_(i=1) ^u ][Σ_(j=1) ^n tan^(−1) ((j/i))−Σ_(j=1) ^v tan^(−1) ((j/i))] The average angle is θ^− =(S/((m+u+1)(n+v+1)))](Q13063.png)
$${Let}'{s}\:{say}\:−{u}\leqslant{x}\leqslant{m}\:{and}\:−{v}\leqslant{y}\leqslant{n}. \\ $$$$ \\ $$$${In}\:{quadrant}\:\mathrm{1}\:{we}\:{have} \\ $$$$\theta_{{ij}} =\mathrm{tan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right)=\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right)=\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}'}{{i}'}\right) \\ $$$${S}_{\mathrm{1}} =\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\theta_{{ij}} =\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right) \\ $$$$ \\ $$$${In}\:{quadrant}\:\mathrm{2}\:{we}\:{have} \\ $$$$\theta_{{ij}} =\mathrm{tan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right)=\pi−\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right)=\pi−\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}'}{{i}'}\right) \\ $$$${S}_{\mathrm{2}} =\underset{{i}=\mathrm{1}} {\overset{{u}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\theta_{{ij}} ={un}\pi−\underset{{i}=\mathrm{1}} {\overset{{u}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right) \\ $$$$ \\ $$$${In}\:{quadrant}\:\mathrm{3}\:{we}\:{have} \\ $$$$\theta_{{ij}} =\mathrm{tan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right)=\pi+\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right)=\pi+\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}'}{{i}'}\right) \\ $$$${S}_{\mathrm{3}} =\underset{{i}=\mathrm{1}} {\overset{{u}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{v}} {\sum}}\theta_{{ij}} ={uv}\pi+\underset{{i}=\mathrm{1}} {\overset{{u}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{v}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right) \\ $$$$ \\ $$$${In}\:{quadrant}\:\mathrm{4}\:{we}\:{have} \\ $$$$\theta_{{ij}} =\mathrm{tan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right)=\mathrm{2}\pi−\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right)=\mathrm{2}\pi−\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}'}{{i}'}\right) \\ $$$${S}_{\mathrm{4}} =\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{v}} {\sum}}\theta_{{ij}} =\mathrm{2}{mv}\pi−\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{v}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right) \\ $$$$ \\ $$$${On}\:+{x}\:{axis}:\:{m}\:{points}\:{with}\:{angle}\:\mathrm{0}, \\ $$$${On}\:+{y}\:{axis}:\:{n}\:{points}\:{with}\:{angle}\:\frac{\pi}{\mathrm{2}}, \\ $$$${On}\:−{x}\:{axis}:\:{u}\:{points}\:{with}\:{angle}\:\pi, \\ $$$${On}\:−{y}\:{axis}:\:{v}\:{points}\:{with}\:{angle}\:\frac{\mathrm{3}\pi}{\mathrm{2}}, \\ $$$${S}_{\mathrm{5}} ={m}×\mathrm{0}+{n}×\frac{\pi}{\mathrm{2}}+{u}\pi+{v}×\frac{\mathrm{3}\pi}{\mathrm{2}}=\frac{\left({n}+\mathrm{2}{u}+\mathrm{3}{v}\right)\pi}{\mathrm{2}} \\ $$$$ \\ $$$${Sum}\:{of}\:{all}\:{angles}: \\ $$$${S}={S}_{\mathrm{1}} +{S}_{\mathrm{2}} +{S}_{\mathrm{3}} +{S}_{\mathrm{4}} +{S}_{\mathrm{5}} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right) \\ $$$$+{un}\pi−\underset{{i}=\mathrm{1}} {\overset{{u}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right) \\ $$$$+{uv}\pi+\underset{{i}=\mathrm{1}} {\overset{{u}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{v}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right) \\ $$$$+\mathrm{2}{mv}\pi−\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}\underset{{j}=\mathrm{1}} {\overset{{v}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right) \\ $$$$+\frac{\left({n}+\mathrm{2}{u}+\mathrm{3}{v}\right)\pi}{\mathrm{2}} \\ $$$$=\frac{\left(\mathrm{2}{un}+\mathrm{2}{uv}+\mathrm{4}{mv}+{n}+\mathrm{2}{u}+\mathrm{3}{v}\right)\pi}{\mathrm{2}} \\ $$$$+\left[\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}−\underset{{i}=\mathrm{1}} {\overset{{u}} {\sum}}\right]\left[\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right)−\underset{{j}=\mathrm{1}} {\overset{{v}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{j}}{{i}}\right)\right] \\ $$$$ \\ $$$${The}\:{average}\:{angle}\:{is} \\ $$$$\overset{−} {\theta}=\frac{{S}}{\left({m}+{u}+\mathrm{1}\right)\left({n}+{v}+\mathrm{1}\right)} \\ $$
