Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 159796 by Ar Brandon last updated on 21/Nov/21

Montrer que la suite de^� finie par u_n =Σ_(k=1) ^n (x^k /k) est une suite de Cauchy.

$$\mathrm{Montrer}\:\mathrm{que}\:\mathrm{la}\:\mathrm{suite}\:\mathrm{d}\acute {\mathrm{e}finie}\:\mathrm{par}\: \\ $$$${u}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{x}^{{k}} }{{k}}\:\mathrm{est}\:\mathrm{une}\:\mathrm{suite}\:\mathrm{de}\:\mathrm{Cauchy}. \\ $$

Answered by alcohol last updated on 21/Nov/21

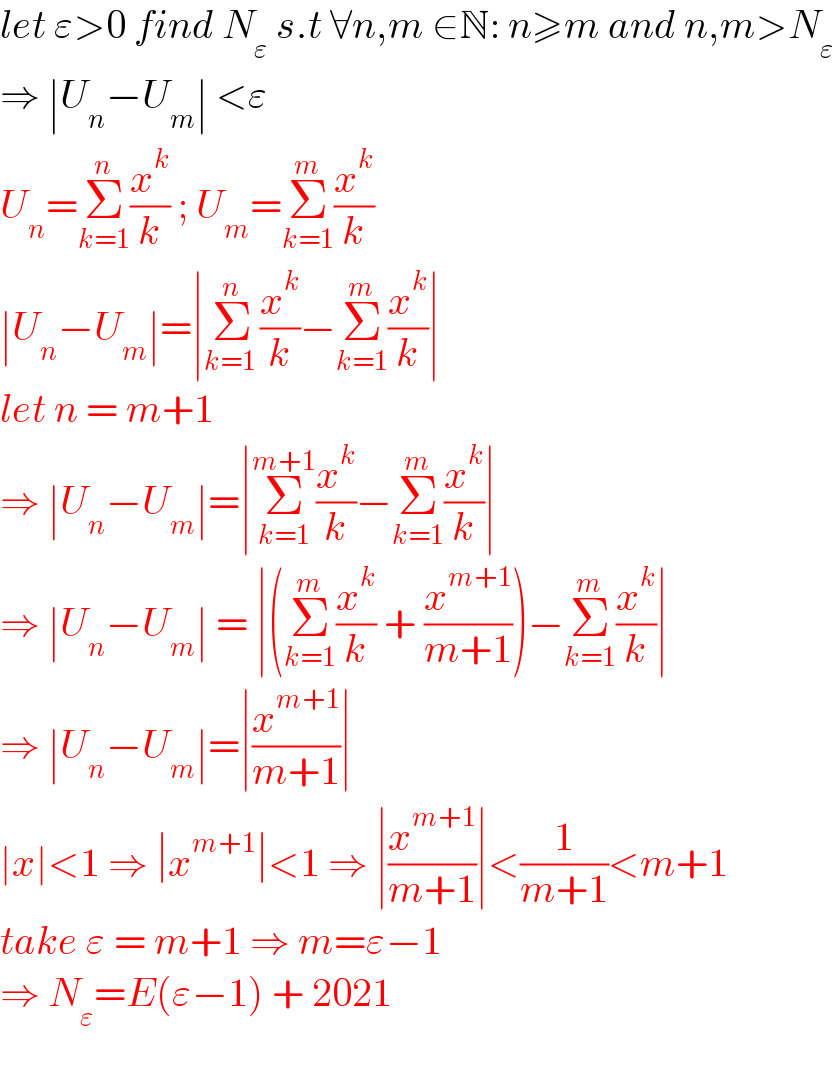
let ε>0 find N_ε s.t ∀n,m ∈N: n≥m and n,m>N_ε ⇒ ∣U_n −U_m ∣ <ε U_n =Σ_(k=1) ^n (x^k /k) ; U_m =Σ_(k=1) ^m (x^k /k) ∣U_n −U_m ∣=∣Σ_(k=1 ) ^n (x^k /k)−Σ_(k=1) ^m (x^k /k)∣ let n = m+1 ⇒ ∣U_n −U_m ∣=∣Σ_(k=1) ^(m+1) (x^k /k)−Σ_(k=1) ^m (x^k /k)∣ ⇒ ∣U_n −U_m ∣ = ∣(Σ_(k=1) ^m (x^k /k) + (x^(m+1) /(m+1)))−Σ_(k=1) ^m (x^k /k)∣ ⇒ ∣U_n −U_m ∣=∣(x^(m+1) /(m+1))∣ ∣x∣<1 ⇒ ∣x^(m+1) ∣<1 ⇒ ∣(x^(m+1) /(m+1))∣<(1/(m+1))<m+1 take ε = m+1 ⇒ m=ε−1 ⇒ N_ε =E(ε−1) + 2021

$${let}\:\varepsilon>\mathrm{0}\:{find}\:{N}_{\varepsilon} \:{s}.{t}\:\forall{n},{m}\:\in\mathbb{N}:\:{n}\geqslant{m}\:{and}\:{n},{m}>{N}_{\varepsilon} \\ $$$$\Rightarrow\:\mid{U}_{{n}} −{U}_{{m}} \mid\:<\varepsilon \\ $$$${U}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{x}^{{k}} }{{k}}\:;\:{U}_{{m}} =\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{x}^{{k}} }{{k}} \\ $$$$\mid{U}_{{n}} −{U}_{{m}} \mid=\mid\underset{{k}=\mathrm{1}\:} {\overset{{n}} {\sum}}\frac{{x}^{{k}} }{{k}}−\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{x}^{{k}} }{{k}}\mid \\ $$$${let}\:{n}\:=\:{m}+\mathrm{1} \\ $$$$\Rightarrow\:\mid{U}_{{n}} −{U}_{{m}} \mid=\mid\underset{{k}=\mathrm{1}} {\overset{{m}+\mathrm{1}} {\sum}}\frac{{x}^{{k}} }{{k}}−\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{x}^{{k}} }{{k}}\mid \\ $$$$\Rightarrow\:\mid{U}_{{n}} −{U}_{{m}} \mid\:=\:\mid\left(\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{x}^{{k}} }{{k}}\:+\:\frac{{x}^{{m}+\mathrm{1}} }{{m}+\mathrm{1}}\right)−\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{{x}^{{k}} }{{k}}\mid \\ $$$$\Rightarrow\:\mid{U}_{{n}} −{U}_{{m}} \mid=\mid\frac{{x}^{{m}+\mathrm{1}} }{{m}+\mathrm{1}}\mid \\ $$$$\mid{x}\mid<\mathrm{1}\:\Rightarrow\:\mid{x}^{{m}+\mathrm{1}} \mid<\mathrm{1}\:\Rightarrow\:\mid\frac{{x}^{{m}+\mathrm{1}} }{{m}+\mathrm{1}}\mid<\frac{\mathrm{1}}{{m}+\mathrm{1}}<{m}+\mathrm{1} \\ $$$${take}\:\varepsilon\:=\:{m}+\mathrm{1}\:\Rightarrow\:{m}=\varepsilon−\mathrm{1} \\ $$$$\Rightarrow\:{N}_{\varepsilon} ={E}\left(\varepsilon−\mathrm{1}\right)\:+\:\mathrm{2021} \\ $$$$ \\ $$

Commented by alcohol last updated on 21/Nov/21

what u asked

$${what}\:{u}\:{asked} \\ $$

Commented by Ar Brandon last updated on 21/Nov/21

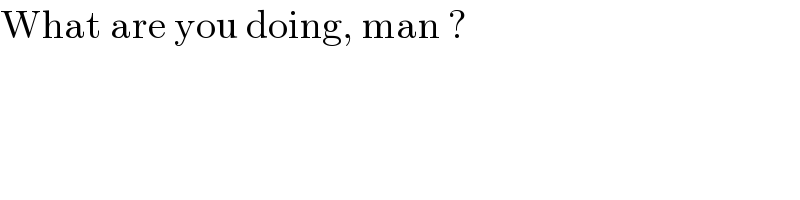
What are you doing, man ?

$$\mathrm{What}\:\mathrm{are}\:\mathrm{you}\:\mathrm{doing},\:\mathrm{man}\:? \\ $$

Commented by Ar Brandon last updated on 21/Nov/21

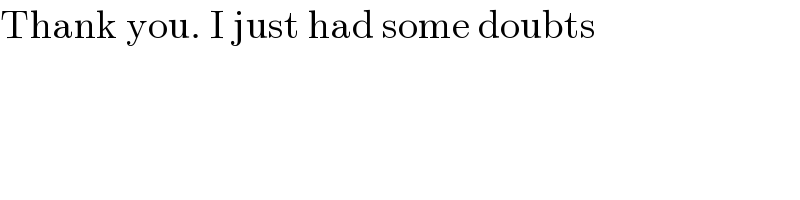
Thank you. I just had some doubts

$$\mathrm{Thank}\:\mathrm{you}.\:\mathrm{I}\:\mathrm{just}\:\mathrm{had}\:\mathrm{some}\:\mathrm{doubts} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com