Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 115815 by Ar Brandon last updated on 28/Sep/20

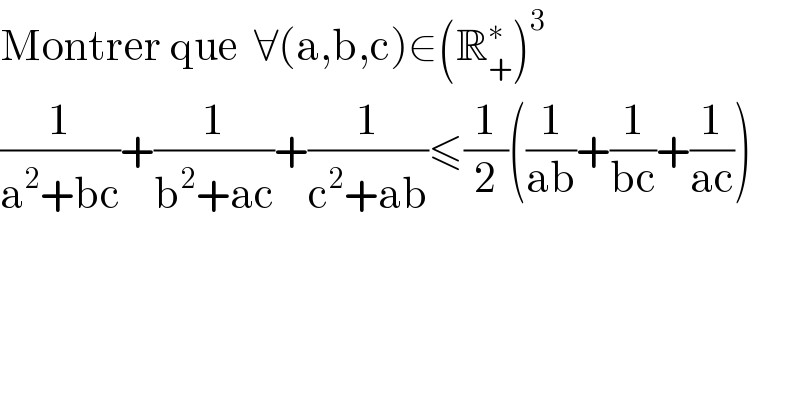
Montrer que ∀(a,b,c)∈(R_+ ^∗ )^3 (1/(a^2 +bc))+(1/(b^2 +ac))+(1/(c^2 +ab))≤(1/2)((1/(ab))+(1/(bc))+(1/(ac)))

$$\mathrm{Montrer}\:\mathrm{que}\:\:\forall\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)\in\left(\mathbb{R}_{+} ^{\ast} \right)^{\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} +\mathrm{bc}}+\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{2}} +\mathrm{ac}}+\frac{\mathrm{1}}{\mathrm{c}^{\mathrm{2}} +\mathrm{ab}}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{ab}}+\frac{\mathrm{1}}{\mathrm{bc}}+\frac{\mathrm{1}}{\mathrm{ac}}\right) \\ $$

Answered by 1549442205PVT last updated on 29/Sep/20

We have: (1/(a^2 +bc))+(1/(b^2 +ac))+(1/(c^2 +ab))≤(1/2)((1/(ab))+(1/(bc))+(1/(ac))) ⇔(1/(a^2 +bc))+(1/(b^2 +ac))+(1/(c^2 +ab))≤((a+b+c)/(2abc))(1) Applying Cauchy′s inequality for two positive numbers we have: a^2 +bc≥2a(√(bc)),b^2 +ac≥2b(√(ac)) c^2 +ab≥2(√(ab)),it follows that L.H.S≤(1/(2a(√(bc))))+(1/(2b(√(ac))))+(1/(2c(√(ab)))) Hence,we just need prove that: (1/(2a(√(bc))))+(1/(2b(√(ac))))+(1/(2c(√(ab))))≤((a+b+c)/(2abc))(2) ⇔(1/( (√a)))+(1/( (√b)))+(1/( (√c)))≤((a+b+c)/( (√(abc)))) ⇔(√(ab))+(√(bc))+(√(ca))≤a+b+c ⇔2((√(ab))+(√(bc))+(√(ca)))≤2(a+b+c) ⇔((√a)−(√b))^2 +((√b)−(√c))^2 +((√c)−(√a))^2 ≥0 This inequality is always true ∀a,b,c>0.Hence,(2)is true infer (1)is true.Thus,the given inequality is proved.The equality ocurrs if and only if a=b=c.(Q.E.D)

$$\mathrm{We}\:\mathrm{have}: \\ $$$$\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} +\mathrm{bc}}+\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{2}} +\mathrm{ac}}+\frac{\mathrm{1}}{\mathrm{c}^{\mathrm{2}} +\mathrm{ab}}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{ab}}+\frac{\mathrm{1}}{\mathrm{bc}}+\frac{\mathrm{1}}{\mathrm{ac}}\right) \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} +\mathrm{bc}}+\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{2}} +\mathrm{ac}}+\frac{\mathrm{1}}{\mathrm{c}^{\mathrm{2}} +\mathrm{ab}}\leqslant\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{2abc}}\left(\mathrm{1}\right) \\ $$$$\mathrm{Applying}\:\mathrm{Cauchy}'\mathrm{s}\:\mathrm{inequality}\:\mathrm{for}\:\mathrm{two} \\ $$$$\mathrm{positive}\:\mathrm{numbers}\:\mathrm{we}\:\mathrm{have}: \\ $$$$\:\mathrm{a}^{\mathrm{2}} +\mathrm{bc}\geqslant\mathrm{2a}\sqrt{\mathrm{bc}},\mathrm{b}^{\mathrm{2}} +\mathrm{ac}\geqslant\mathrm{2b}\sqrt{\mathrm{ac}} \\ $$$$\mathrm{c}^{\mathrm{2}} +\mathrm{ab}\geqslant\mathrm{2}\sqrt{\mathrm{ab}},\mathrm{it}\:\mathrm{follows}\:\mathrm{that} \\ $$$$\mathrm{L}.\mathrm{H}.\mathrm{S}\leqslant\frac{\mathrm{1}}{\mathrm{2a}\sqrt{\mathrm{bc}}}+\frac{\mathrm{1}}{\mathrm{2b}\sqrt{\mathrm{ac}}}+\frac{\mathrm{1}}{\mathrm{2c}\sqrt{\mathrm{ab}}} \\ $$$$\mathrm{Hence},\mathrm{we}\:\mathrm{just}\:\mathrm{need}\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{1}}{\mathrm{2a}\sqrt{\mathrm{bc}}}+\frac{\mathrm{1}}{\mathrm{2b}\sqrt{\mathrm{ac}}}+\frac{\mathrm{1}}{\mathrm{2c}\sqrt{\mathrm{ab}}}\leqslant\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{2abc}}\left(\mathrm{2}\right) \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{b}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{c}}}\leqslant\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\:\sqrt{\mathrm{abc}}} \\ $$$$\Leftrightarrow\sqrt{\mathrm{ab}}+\sqrt{\mathrm{bc}}+\sqrt{\mathrm{ca}}\leqslant\mathrm{a}+\mathrm{b}+\mathrm{c} \\ $$$$\Leftrightarrow\mathrm{2}\left(\sqrt{\mathrm{ab}}+\sqrt{\mathrm{bc}}+\sqrt{\mathrm{ca}}\right)\leqslant\mathrm{2}\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right) \\ $$$$\Leftrightarrow\left(\sqrt{\mathrm{a}}−\sqrt{\mathrm{b}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{b}}−\sqrt{\mathrm{c}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{c}}−\sqrt{\mathrm{a}}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{always}\:\mathrm{true} \\ $$$$\forall\mathrm{a},\mathrm{b},\mathrm{c}>\mathrm{0}.\mathrm{Hence},\left(\mathrm{2}\right)\mathrm{is}\:\mathrm{true}\:\mathrm{infer}\:\left(\mathrm{1}\right)\mathrm{is}\: \\ $$$$\mathrm{true}.\mathrm{Thus},\mathrm{the}\:\mathrm{given}\:\mathrm{inequality}\:\mathrm{is} \\ $$$$\mathrm{proved}.\mathrm{The}\:\mathrm{equality}\:\mathrm{ocurrs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only} \\ $$$$\mathrm{if}\:\mathrm{a}=\mathrm{b}=\mathrm{c}.\left(\boldsymbol{\mathrm{Q}}.\boldsymbol{\mathrm{E}}.\boldsymbol{\mathrm{D}}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com