
Question Number 183633 by a.lgnaoui last updated on 27/Dec/22
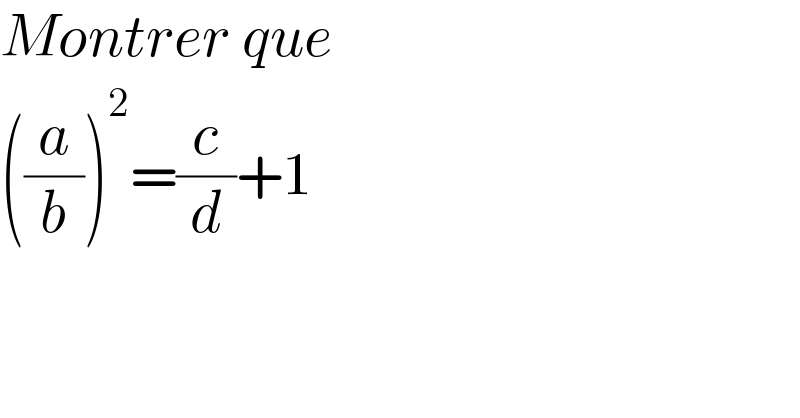
$${Montrer}\:{que} \\ $$$$\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} =\frac{{c}}{{d}}+\mathrm{1} \\ $$
Commented by a.lgnaoui last updated on 27/Dec/22
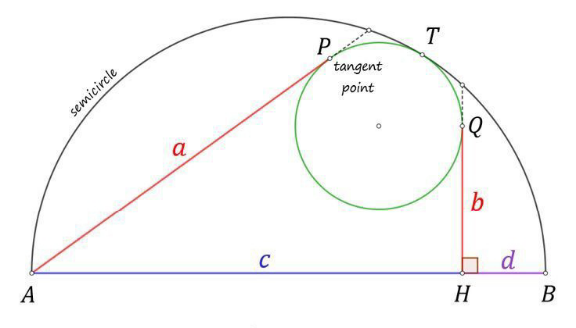
Answered by mr W last updated on 28/Dec/22
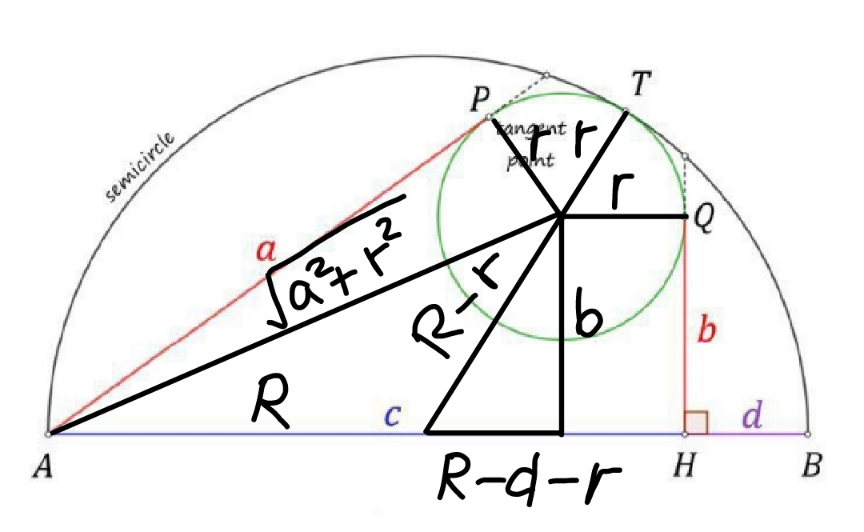
Commented by mr W last updated on 28/Dec/22
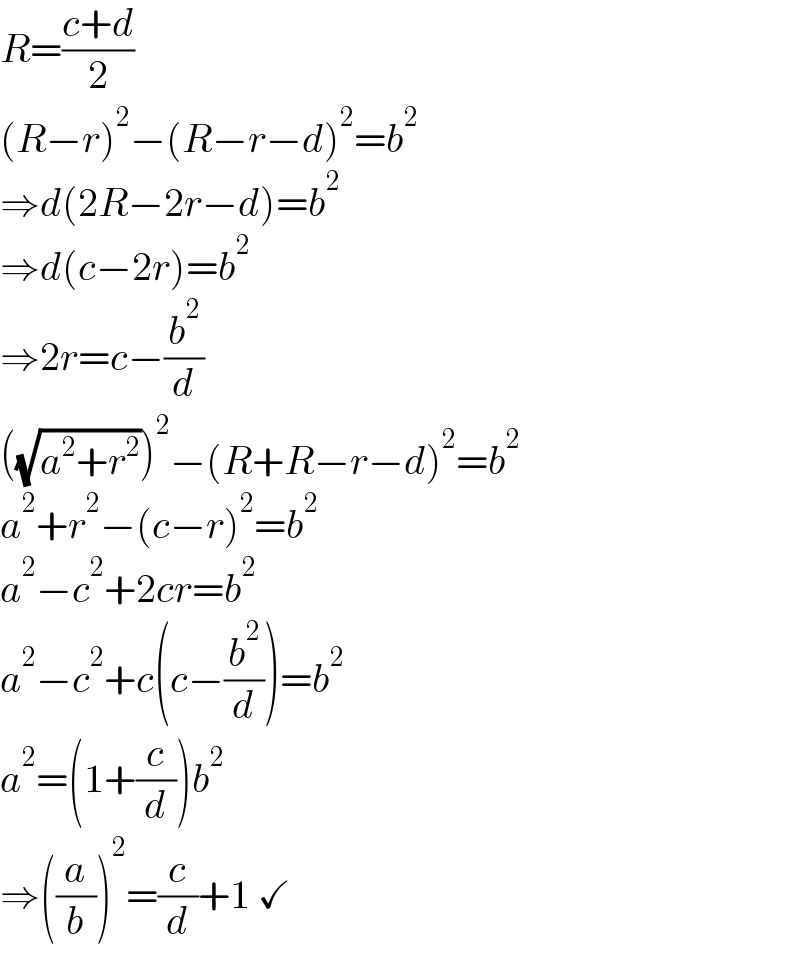
$${R}=\frac{{c}+{d}}{\mathrm{2}} \\ $$$$\left({R}−{r}\right)^{\mathrm{2}} −\left({R}−{r}−{d}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$$\Rightarrow{d}\left(\mathrm{2}{R}−\mathrm{2}{r}−{d}\right)={b}^{\mathrm{2}} \\ $$$$\Rightarrow{d}\left({c}−\mathrm{2}{r}\right)={b}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{r}={c}−\frac{{b}^{\mathrm{2}} }{{d}} \\ $$$$\left(\sqrt{{a}^{\mathrm{2}} +{r}^{\mathrm{2}} }\right)^{\mathrm{2}} −\left({R}+{R}−{r}−{d}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{r}^{\mathrm{2}} −\left({c}−{r}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} −{c}^{\mathrm{2}} +\mathrm{2}{cr}={b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} −{c}^{\mathrm{2}} +{c}\left({c}−\frac{{b}^{\mathrm{2}} }{{d}}\right)={b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} =\left(\mathrm{1}+\frac{{c}}{{d}}\right){b}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} =\frac{{c}}{{d}}+\mathrm{1}\:\checkmark \\ $$
