
Question Number 187142 by a.lgnaoui last updated on 14/Feb/23
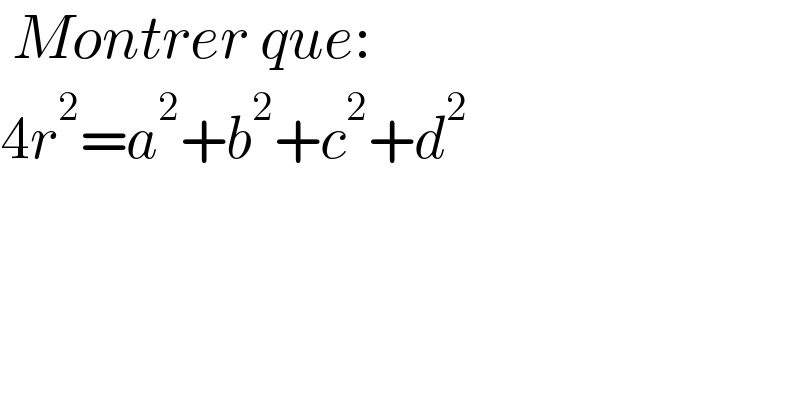
$$\:{Montrer}\:{que}: \\ $$$$\mathrm{4}{r}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 14/Feb/23
Commented by mahdipoor last updated on 14/Feb/23
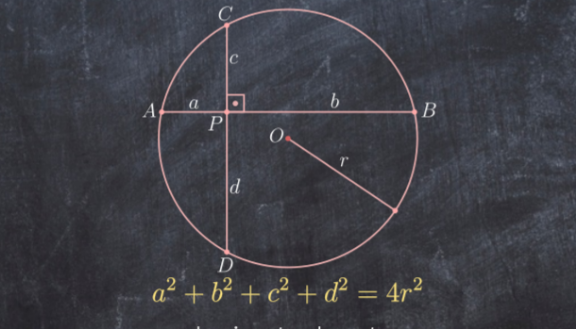
![C(O,r) : x^2 +y^2 =r^2 P=(i,j) { ((line CPD : x=i)),((line APB : y=j)) :} A=(−(√(r^2 −j^2 )),j) B=(+(√(r^2 −j^2 )),j) C=(i,(√(r^2 −i^2 ))) D=(i,−(√(r^2 −i^2 ))) a^2 +b^2 +c^2 +d^2 =∣AP∣^2 +∣AB∣^2 +...= [(i−(−(√(r^2 −j^2 ))))^2 +(j−j)^2 ]+[(i−(√(r^2 −j^2 )))^2 +(j−j)^2 ] +...=2i^2 +2(r^2 −j^2 )+2j^2 +2(r^2 −i^2 )=4r^2](Q187160.png)
$${C}\left({O},{r}\right)\::\:\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${P}=\left({i},{j}\right)\begin{cases}{{line}\:{CPD}\::\:{x}={i}}\\{{line}\:{APB}\::\:{y}={j}}\end{cases} \\ $$$${A}=\left(−\sqrt{{r}^{\mathrm{2}} −{j}^{\mathrm{2}} },{j}\right)\:\:\:\:\:\:\:\:{B}=\left(+\sqrt{{r}^{\mathrm{2}} −{j}^{\mathrm{2}} },{j}\right) \\ $$$${C}=\left({i},\sqrt{{r}^{\mathrm{2}} −{i}^{\mathrm{2}} }\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:{D}=\left({i},−\sqrt{{r}^{\mathrm{2}} −{i}^{\mathrm{2}} }\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mid{AP}\mid^{\mathrm{2}} +\mid{AB}\mid^{\mathrm{2}} +...= \\ $$$$\left[\left({i}−\left(−\sqrt{{r}^{\mathrm{2}} −{j}^{\mathrm{2}} }\right)\right)^{\mathrm{2}} +\left({j}−{j}\right)^{\mathrm{2}} \right]+\left[\left({i}−\sqrt{{r}^{\mathrm{2}} −{j}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left({j}−{j}\right)^{\mathrm{2}} \right] \\ $$$$+...=\mathrm{2}{i}^{\mathrm{2}} +\mathrm{2}\left({r}^{\mathrm{2}} −{j}^{\mathrm{2}} \right)+\mathrm{2}{j}^{\mathrm{2}} +\mathrm{2}\left({r}^{\mathrm{2}} −{i}^{\mathrm{2}} \right)=\mathrm{4}{r}^{\mathrm{2}} \\ $$
Answered by mr W last updated on 14/Feb/23
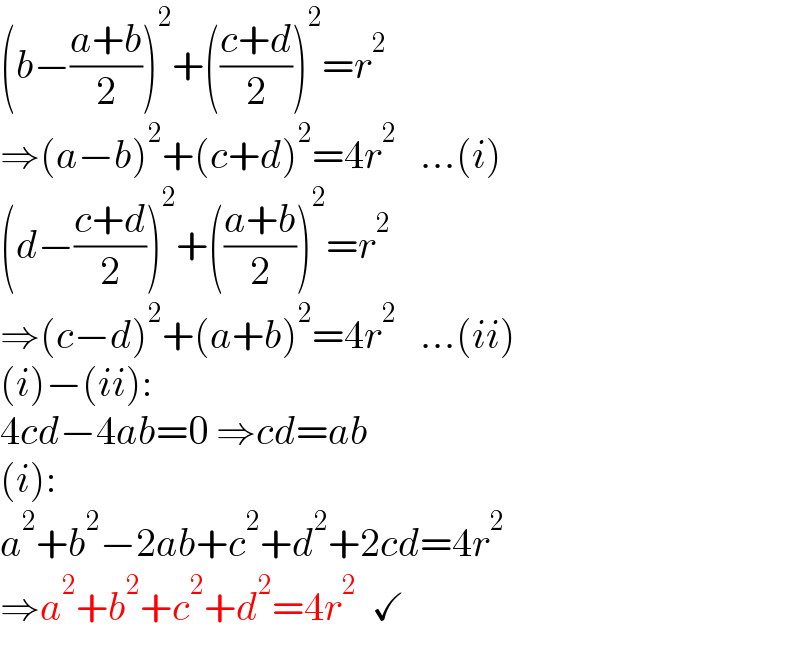
$$\left({b}−\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{c}+{d}}{\mathrm{2}}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\left({a}−{b}\right)^{\mathrm{2}} +\left({c}+{d}\right)^{\mathrm{2}} =\mathrm{4}{r}^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$$$\left({d}−\frac{{c}+{d}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \: \\ $$$$\Rightarrow\left({c}−{d}\right)^{\mathrm{2}} +\left({a}+{b}\right)^{\mathrm{2}} =\mathrm{4}{r}^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\mathrm{4}{cd}−\mathrm{4}{ab}=\mathrm{0}\:\Rightarrow{cd}={ab} \\ $$$$\left({i}\right): \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}+{c}^{\mathrm{2}} +{d}^{\mathrm{2}} +\mathrm{2}{cd}=\mathrm{4}{r}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} =\mathrm{4}{r}^{\mathrm{2}} \:\:\checkmark \\ $$
