Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 62942 by Tawa1 last updated on 27/Jun/19

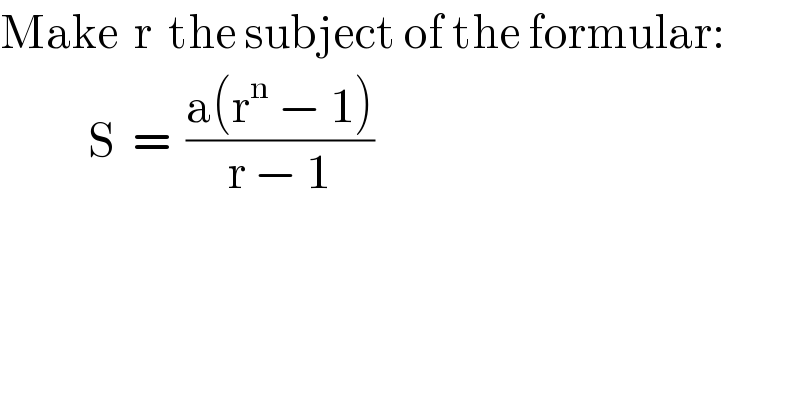
Make r the subject of the formular: S = ((a(r^n − 1))/(r − 1))

$$\mathrm{Make}\:\:\mathrm{r}\:\:\mathrm{the}\:\mathrm{subject}\:\mathrm{of}\:\mathrm{the}\:\mathrm{formular}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{S}\:\:=\:\:\frac{\mathrm{a}\left(\mathrm{r}^{\mathrm{n}} \:−\:\mathrm{1}\right)}{\mathrm{r}\:−\:\mathrm{1}} \\ $$

Commented by Tawa1 last updated on 27/Jun/19

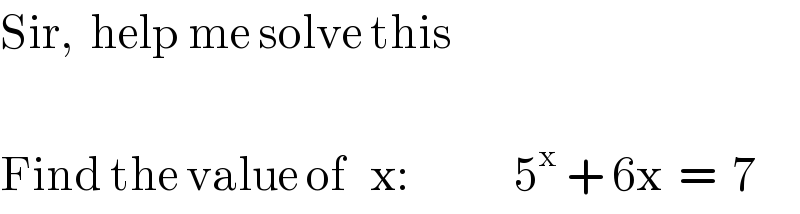
Sir, help me solve this Find the value of x: 5^x + 6x = 7

$$\mathrm{Sir},\:\:\mathrm{help}\:\mathrm{me}\:\mathrm{solve}\:\mathrm{this} \\ $$$$\:\:\:\:\:\:\: \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:\:\mathrm{x}:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}^{\mathrm{x}} \:+\:\mathrm{6x}\:\:=\:\:\mathrm{7} \\ $$

Commented by Tawa1 last updated on 27/Jun/19

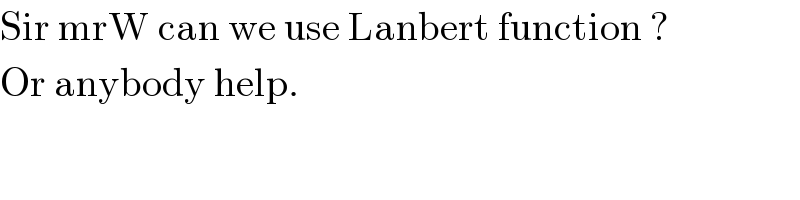
Sir mrW can we use Lanbert function ? Or anybody help.

$$\mathrm{Sir}\:\mathrm{mrW}\:\mathrm{can}\:\mathrm{we}\:\mathrm{use}\:\mathrm{Lanbert}\:\mathrm{function}\:? \\ $$$$\mathrm{Or}\:\mathrm{anybody}\:\mathrm{help}. \\ $$

Commented by mr W last updated on 27/Jun/19

no

$${no} \\ $$

Commented by Tawa1 last updated on 27/Jun/19

Thank you sir. God bless you

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$

Commented by mr W last updated on 27/Jun/19

5^x +6x=7 5^x =6((7/6)−x) ((7/6)−x)5^(−x) =(1/6) ((7/6)−x)5^((7/6)−x) =(1/6)×5^(7/6) ((7/6)−x)e^(((7/6)−x)ln 5) =(1/6)×5^(7/6) [((7/6)−x)ln 5]e^(((7/6)−x)ln 5) =(1/6)×5^(7/6) ×ln 5 ⇒((7/6)−x)ln 5=W((1/6)×5^(7/6) ×ln 5) ⇒x=(7/6)−(1/(ln 5))W((1/6)×5^(7/6) ×ln 5) ⇒≈(7/6)−((0.7933)/(ln 5))=0.6737

$$\mathrm{5}^{{x}} +\mathrm{6}{x}=\mathrm{7} \\ $$$$\mathrm{5}^{{x}} =\mathrm{6}\left(\frac{\mathrm{7}}{\mathrm{6}}−{x}\right) \\ $$$$\left(\frac{\mathrm{7}}{\mathrm{6}}−{x}\right)\mathrm{5}^{−{x}} =\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\left(\frac{\mathrm{7}}{\mathrm{6}}−{x}\right)\mathrm{5}^{\frac{\mathrm{7}}{\mathrm{6}}−{x}} =\frac{\mathrm{1}}{\mathrm{6}}×\mathrm{5}^{\frac{\mathrm{7}}{\mathrm{6}}} \\ $$$$\left(\frac{\mathrm{7}}{\mathrm{6}}−{x}\right){e}^{\left(\frac{\mathrm{7}}{\mathrm{6}}−{x}\right)\mathrm{ln}\:\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{6}}×\mathrm{5}^{\frac{\mathrm{7}}{\mathrm{6}}} \\ $$$$\left[\left(\frac{\mathrm{7}}{\mathrm{6}}−{x}\right)\mathrm{ln}\:\mathrm{5}\right]{e}^{\left(\frac{\mathrm{7}}{\mathrm{6}}−{x}\right)\mathrm{ln}\:\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{6}}×\mathrm{5}^{\frac{\mathrm{7}}{\mathrm{6}}} ×\mathrm{ln}\:\mathrm{5} \\ $$$$\Rightarrow\left(\frac{\mathrm{7}}{\mathrm{6}}−{x}\right)\mathrm{ln}\:\mathrm{5}={W}\left(\frac{\mathrm{1}}{\mathrm{6}}×\mathrm{5}^{\frac{\mathrm{7}}{\mathrm{6}}} ×\mathrm{ln}\:\mathrm{5}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{7}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{5}}\mathbb{W}\left(\frac{\mathrm{1}}{\mathrm{6}}×\mathrm{5}^{\frac{\mathrm{7}}{\mathrm{6}}} ×\mathrm{ln}\:\mathrm{5}\right) \\ $$$$\Rightarrow\approx\frac{\mathrm{7}}{\mathrm{6}}−\frac{\mathrm{0}.\mathrm{7933}}{\mathrm{ln}\:\mathrm{5}}=\mathrm{0}.\mathrm{6737} \\ $$

Commented by kaivan.ahmadi last updated on 27/Jun/19

5^x =7−6x if we plote y_1 =5^x and y_2 =7−6x then we see that they cut off each othere at one point,this means that this equation has one root. now if f(x)=5^x +6x−7=0 {: ((f(0)<0)),((f(1)>0)) }⇒f(0)f(1)<0 f((1/2))<0 so the root is between ((1/2),1) f((3/4))>0 so the root is between ((1/2),(3/4))

$$\mathrm{5}^{{x}} =\mathrm{7}−\mathrm{6}{x} \\ $$$${if}\:{we}\:{plote}\:{y}_{\mathrm{1}} =\mathrm{5}^{{x}} \:{and}\:{y}_{\mathrm{2}} =\mathrm{7}−\mathrm{6}{x}\:{then}\:{we}\:{see}\:{that} \\ $$$${they}\:{cut}\:{off}\:{each}\:{othere}\:{at}\:{one}\:{point},{this} \\ $$$${means}\:{that}\:{this}\:{equation}\:{has}\:{one}\:{root}. \\ $$$${now}\:{if} \\ $$$${f}\left({x}\right)=\mathrm{5}^{{x}} +\mathrm{6}{x}−\mathrm{7}=\mathrm{0} \\ $$$$ \\ $$$$\left.\begin{matrix}{{f}\left(\mathrm{0}\right)<\mathrm{0}}\\{{f}\left(\mathrm{1}\right)>\mathrm{0}}\end{matrix}\right\}\Rightarrow{f}\left(\mathrm{0}\right){f}\left(\mathrm{1}\right)<\mathrm{0} \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)<\mathrm{0} \\ $$$${so}\:{the}\:{root}\:{is}\:{between}\:\left(\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}\right) \\ $$$${f}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)>\mathrm{0} \\ $$$${so}\:{the}\:{root}\:{is}\:{between}\:\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Hope last updated on 27/Jun/19

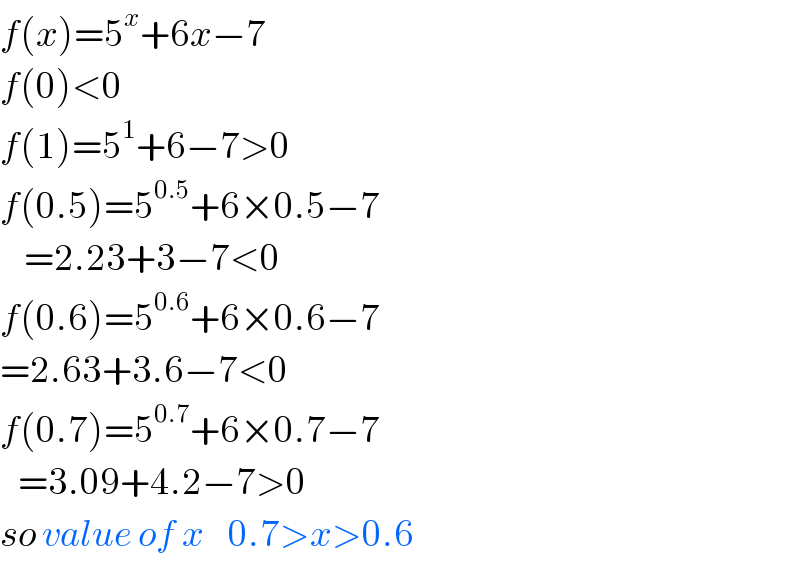
f(x)=5^x +6x−7 f(0)<0 f(1)=5^1 +6−7>0 f(0.5)=5^(0.5) +6×0.5−7 =2.23+3−7<0 f(0.6)=5^(0.6) +6×0.6−7 =2.63+3.6−7<0 f(0.7)=5^(0.7) +6×0.7−7 =3.09+4.2−7>0 so value of x 0.7>x>0.6

$${f}\left({x}\right)=\mathrm{5}^{{x}} +\mathrm{6}{x}−\mathrm{7} \\ $$$${f}\left(\mathrm{0}\right)<\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{5}^{\mathrm{1}} +\mathrm{6}−\mathrm{7}>\mathrm{0} \\ $$$${f}\left(\mathrm{0}.\mathrm{5}\right)=\mathrm{5}^{\mathrm{0}.\mathrm{5}} +\mathrm{6}×\mathrm{0}.\mathrm{5}−\mathrm{7} \\ $$$$\:\:\:\:=\mathrm{2}.\mathrm{23}+\mathrm{3}−\mathrm{7}<\mathrm{0} \\ $$$${f}\left(\mathrm{0}.\mathrm{6}\right)=\mathrm{5}^{\mathrm{0}.\mathrm{6}} +\mathrm{6}×\mathrm{0}.\mathrm{6}−\mathrm{7} \\ $$$$=\mathrm{2}.\mathrm{63}+\mathrm{3}.\mathrm{6}−\mathrm{7}<\mathrm{0} \\ $$$${f}\left(\mathrm{0}.\mathrm{7}\right)=\mathrm{5}^{\mathrm{0}.\mathrm{7}} +\mathrm{6}×\mathrm{0}.\mathrm{7}−\mathrm{7} \\ $$$$\:\:\:=\mathrm{3}.\mathrm{09}+\mathrm{4}.\mathrm{2}−\mathrm{7}>\mathrm{0} \\ $$$${so}\:{value}\:{of}\:{x}\:\:\:\:\mathrm{0}.\mathrm{7}>{x}>\mathrm{0}.\mathrm{6} \\ $$

Commented by Tawa1 last updated on 27/Jun/19

Wow, God bless you sir

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 27/Jun/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Tawa1 last updated on 27/Jun/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by peter frank last updated on 27/Jun/19

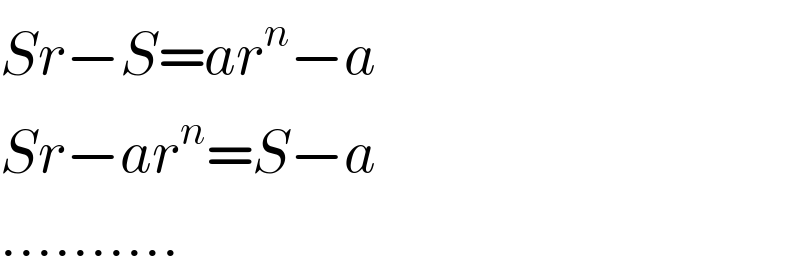
Sr−S=ar^n −a Sr−ar^n =S−a ..........

$${Sr}−{S}={ar}^{{n}} −{a} \\ $$$${Sr}−{ar}^{{n}} ={S}−{a} \\ $$$$.......... \\ $$

Commented by Tawa1 last updated on 27/Jun/19

How to find r sir

$$\mathrm{How}\:\mathrm{to}\:\mathrm{find}\:\:\mathrm{r}\:\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com