
Question Number 209860 by lmcp1203 last updated on 23/Jul/24

$$ \\ $$$$\mathrm{Magnitude}\:\mathrm{A}\:\mathrm{varies}\:\mathrm{proportionally}\:\mathrm{with}\:\left(\mathrm{B}\:\mathrm{squared}\:+\:\mathrm{4}\right)\:\mathrm{and}\:\mathrm{magnitude}\:\mathrm{B}\:\mathrm{varies}\:\mathrm{proportionally}\:\mathrm{with} \\ $$$$\left({t}\mathrm{he}\:\mathrm{root}\:\mathrm{of}\:\mathrm{C}\right)\:−\:\mathrm{5}.\:\mathrm{Also}\:\mathrm{when}\:\mathrm{A}\:\mathrm{is}\:\mathrm{16}\:,\:\mathrm{B}\:\mathrm{is}\:\mathrm{12}\:\mathrm{and}\:\mathrm{C}\:\mathrm{takes}\:\mathrm{the}\:\mathrm{value}\:\mathrm{81}.\:\mathrm{Calculate}\:\mathrm{the}\:\mathrm{value}\:\mathrm{that}\:\mathrm{A}\:\mathrm{takes} \\ $$$$\mathrm{wh}{e}\mathrm{n}\:\mathrm{C}\:\mathrm{is}\:\mathrm{49}.\:\:\:{help}\:\:{me}.\:{please}.\:{thanks} \\ $$
Answered by mr W last updated on 23/Jul/24
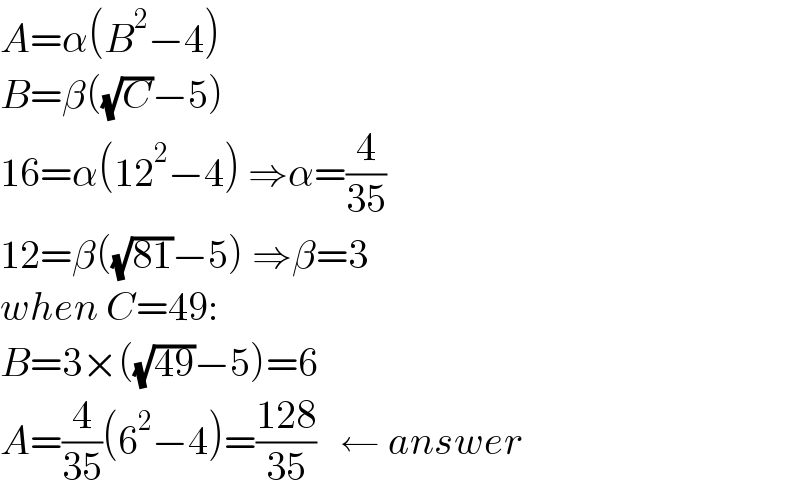
$${A}=\alpha\left({B}^{\mathrm{2}} −\mathrm{4}\right) \\ $$$${B}=\beta\left(\sqrt{{C}}−\mathrm{5}\right) \\ $$$$\mathrm{16}=\alpha\left(\mathrm{12}^{\mathrm{2}} −\mathrm{4}\right)\:\Rightarrow\alpha=\frac{\mathrm{4}}{\mathrm{35}} \\ $$$$\mathrm{12}=\beta\left(\sqrt{\mathrm{81}}−\mathrm{5}\right)\:\Rightarrow\beta=\mathrm{3} \\ $$$${when}\:{C}=\mathrm{49}: \\ $$$${B}=\mathrm{3}×\left(\sqrt{\mathrm{49}}−\mathrm{5}\right)=\mathrm{6} \\ $$$${A}=\frac{\mathrm{4}}{\mathrm{35}}\left(\mathrm{6}^{\mathrm{2}} −\mathrm{4}\right)=\frac{\mathrm{128}}{\mathrm{35}}\:\:\:\leftarrow\:{answer} \\ $$
Answered by lmcp1203 last updated on 23/Jul/24

$${thank}\:{you}.\: \\ $$
