
Question Number 194821 by sniper237 last updated on 16/Jul/23

$${M}\:{a}\:{inside}\:{poin}\:{in}\:\:\Delta{ABC}. \\ $$$${M}\:=\:{bar}\:\left\{\left({A},\:{area}\left({MBC}\right)\right),\:\left({B},\:{area}\left({MAC}\right)\right),\left({C},{area}\left({MAB}\right)\right)\right\} \\ $$
Commented by mr W last updated on 16/Jul/23
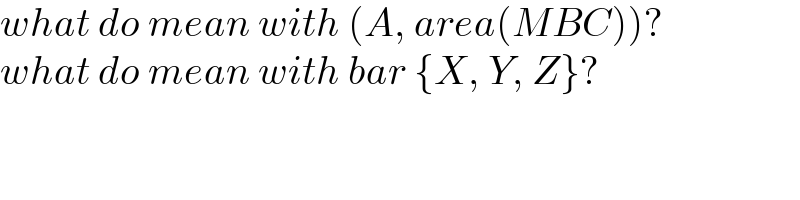
$${what}\:{do}\:{mean}\:{with}\:\left({A},\:{area}\left({MBC}\right)\right)? \\ $$$${what}\:{do}\:{mean}\:{with}\:{bar}\:\left\{{X},\:{Y},\:{Z}\right\}? \\ $$
Commented by sniper237 last updated on 16/Jul/23
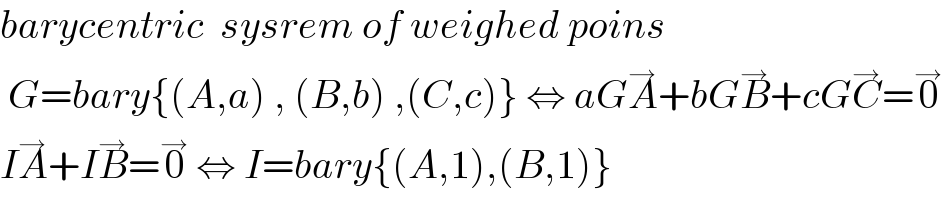
$${barycentric}\:\:{sysrem}\:{of}\:{weighed}\:{poins} \\ $$$$\:{G}={bary}\left\{\left({A},{a}\right)\:,\:\left({B},{b}\right)\:,\left({C},{c}\right)\right\}\:\Leftrightarrow\:{aG}\overset{\rightarrow} {{A}}+{bG}\overset{\rightarrow} {{B}}+{cG}\overset{\rightarrow} {{C}}=\overset{\rightarrow} {\mathrm{0}} \\ $$$${I}\overset{\rightarrow} {{A}}+{I}\overset{\rightarrow} {{B}}=\overset{\rightarrow} {\mathrm{0}}\:\Leftrightarrow\:{I}={bary}\left\{\left({A},\mathrm{1}\right),\left({B},\mathrm{1}\right)\right\} \\ $$
