Question and Answers Forum

LogicQuestion and Answers: Page 5

Question Number 46631 Answers: 0 Comments: 1

Question Number 44584 Answers: 1 Comments: 5

Prove that if a, b, c ∈ Z and a^2 + b^2 = c^2 , then 3 ∣ ab

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{if}\:\:{a},\:{b},\:{c}\:\in\:\mathbb{Z}\:\:\mathrm{and}\:\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:=\:{c}^{\mathrm{2}} ,\:\mathrm{then} \\ $$$$\mathrm{3}\:\mid\:{ab} \\ $$

Question Number 36450 Answers: 1 Comments: 2

Question Number 35562 Answers: 0 Comments: 2

Is there a backwards “⇒”?

$$\mathrm{Is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{backwards}\:``\Rightarrow''? \\ $$

Question Number 33217 Answers: 0 Comments: 7

Question Number 33216 Answers: 1 Comments: 0

Question Number 29308 Answers: 2 Comments: 0

Solve: w^3 = − 16

$$\mathrm{Solve}:\:\:\:\mathrm{w}^{\mathrm{3}} \:=\:−\:\mathrm{16} \\ $$

Question Number 28302 Answers: 0 Comments: 1

Question Number 26721 Answers: 0 Comments: 1

−2y(y−12)(y−1)or(y−12)(−2y^2 −2y) both are same.

$$−\mathrm{2}{y}\left({y}−\mathrm{12}\right)\left({y}−\mathrm{1}\right){or}\left({y}−\mathrm{12}\right)\left(−\mathrm{2}{y}^{\mathrm{2}} −\mathrm{2}{y}\right)\:\:{both}\:{are}\:{same}. \\ $$

Question Number 24211 Answers: 1 Comments: 13

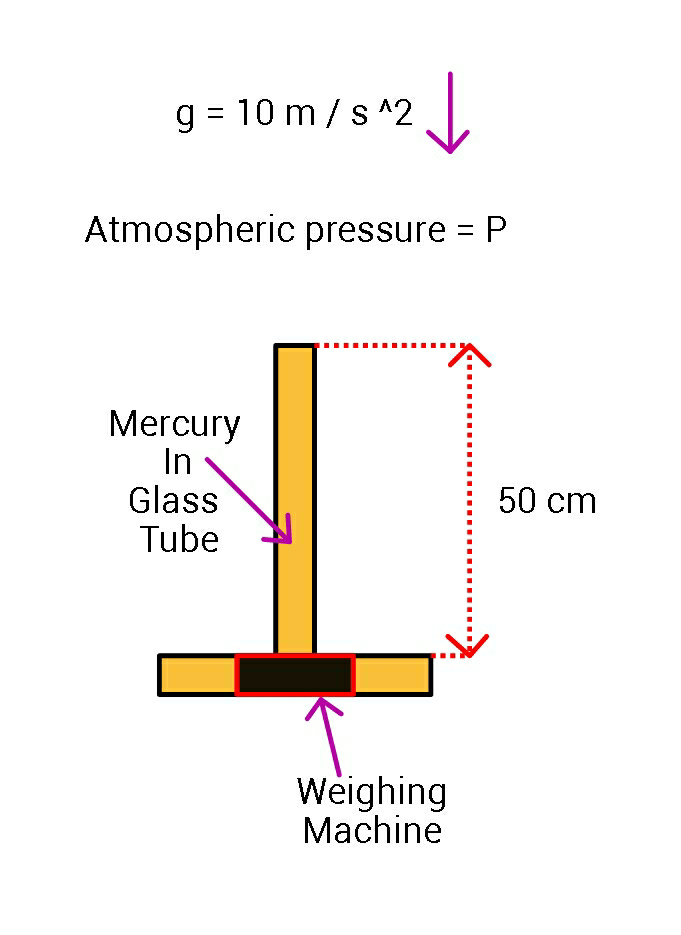
Question Number 23508 Answers: 1 Comments: 1

Question Number 22872 Answers: 1 Comments: 4

Question Number 19516 Answers: 1 Comments: 0

Let Akbar and Birbal together have n marbles, where n > 0. Akbar says to Birbal, “If I give you some marbles then you will have twice as many marbles as I will have.” Birbal says to Akbar, “If I give you some marbles then you will have thrice as many marbles as I will have.” What is the minimum possible value of n for which the above statements are true?

$$\mathrm{Let}\:\mathrm{Akbar}\:\mathrm{and}\:\mathrm{Birbal}\:\mathrm{together}\:\mathrm{have}\:{n} \\ $$$$\mathrm{marbles},\:\mathrm{where}\:{n}\:>\:\mathrm{0}. \\ $$$$\mathrm{Akbar}\:\mathrm{says}\:\mathrm{to}\:\mathrm{Birbal},\:``\mathrm{If}\:\mathrm{I}\:\mathrm{give}\:\mathrm{you}\:\mathrm{some} \\ $$$$\mathrm{marbles}\:\mathrm{then}\:\mathrm{you}\:\mathrm{will}\:\mathrm{have}\:\mathrm{twice}\:\mathrm{as} \\ $$$$\mathrm{many}\:\mathrm{marbles}\:\mathrm{as}\:\mathrm{I}\:\mathrm{will}\:\mathrm{have}.''\:\mathrm{Birbal} \\ $$$$\mathrm{says}\:\mathrm{to}\:\mathrm{Akbar},\:``\mathrm{If}\:\mathrm{I}\:\mathrm{give}\:\mathrm{you}\:\mathrm{some} \\ $$$$\mathrm{marbles}\:\mathrm{then}\:\mathrm{you}\:\mathrm{will}\:\mathrm{have}\:\mathrm{thrice}\:\mathrm{as} \\ $$$$\mathrm{many}\:\mathrm{marbles}\:\mathrm{as}\:\mathrm{I}\:\mathrm{will}\:\mathrm{have}.'' \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{possible}\:\mathrm{value}\:\mathrm{of} \\ $$$${n}\:\mathrm{for}\:\mathrm{which}\:\mathrm{the}\:\mathrm{above}\:\mathrm{statements}\:\mathrm{are} \\ $$$$\mathrm{true}? \\ $$

Question Number 18133 Answers: 1 Comments: 0

A 4×4×4 wooden cube is painted so that one pair of opposite faces is blue, one pair green and one pair red. The cube is now sliced into 64 cubes of side 1 unit each. (i) How many of the smaller cubes have no painted face? (ii) How many of the smaller cubes have exactly one painted face? (iii) How many of the smaller cubes have exactly two painted face? (iv) How many of the smaller cubes have exactly three painted face? (v) How many of the smaller cubes have exactly one face painted blue and one face painted green?

$$\mathrm{A}\:\mathrm{4}×\mathrm{4}×\mathrm{4}\:\mathrm{wooden}\:\mathrm{cube}\:\mathrm{is}\:\mathrm{painted}\:\mathrm{so} \\ $$$$\mathrm{that}\:\mathrm{one}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{opposite}\:\mathrm{faces}\:\mathrm{is}\:\mathrm{blue}, \\ $$$$\mathrm{one}\:\mathrm{pair}\:\mathrm{green}\:\mathrm{and}\:\mathrm{one}\:\mathrm{pair}\:\mathrm{red}.\:\mathrm{The} \\ $$$$\mathrm{cube}\:\mathrm{is}\:\mathrm{now}\:\mathrm{sliced}\:\mathrm{into}\:\mathrm{64}\:\mathrm{cubes}\:\mathrm{of}\:\mathrm{side} \\ $$$$\mathrm{1}\:\mathrm{unit}\:\mathrm{each}. \\ $$$$\left(\mathrm{i}\right)\:\mathrm{How}\:\mathrm{many}\:\mathrm{of}\:\mathrm{the}\:\mathrm{smaller}\:\mathrm{cubes}\:\mathrm{have} \\ $$$$\mathrm{no}\:\mathrm{painted}\:\mathrm{face}? \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{How}\:\mathrm{many}\:\mathrm{of}\:\mathrm{the}\:\mathrm{smaller}\:\mathrm{cubes}\:\mathrm{have} \\ $$$$\mathrm{exactly}\:\mathrm{one}\:\mathrm{painted}\:\mathrm{face}? \\ $$$$\left(\mathrm{iii}\right)\:\mathrm{How}\:\mathrm{many}\:\mathrm{of}\:\mathrm{the}\:\mathrm{smaller}\:\mathrm{cubes}\:\mathrm{have} \\ $$$$\mathrm{exactly}\:\mathrm{two}\:\mathrm{painted}\:\mathrm{face}? \\ $$$$\left(\mathrm{iv}\right)\:\mathrm{How}\:\mathrm{many}\:\mathrm{of}\:\mathrm{the}\:\mathrm{smaller}\:\mathrm{cubes}\:\mathrm{have} \\ $$$$\mathrm{exactly}\:\mathrm{three}\:\mathrm{painted}\:\mathrm{face}? \\ $$$$\left(\mathrm{v}\right)\:\mathrm{How}\:\mathrm{many}\:\mathrm{of}\:\mathrm{the}\:\mathrm{smaller}\:\mathrm{cubes}\:\mathrm{have} \\ $$$$\mathrm{exactly}\:\mathrm{one}\:\mathrm{face}\:\mathrm{painted}\:\mathrm{blue}\:\mathrm{and}\:\mathrm{one} \\ $$$$\mathrm{face}\:\mathrm{painted}\:\mathrm{green}? \\ $$

Question Number 17729 Answers: 1 Comments: 3

A lotus plant in a pool of water is (1/2) cubit above water level. When propelled by air, the lotus sinks in the pool 2 cubits away from its position. Find the depth of water in the pool.

$$\mathrm{A}\:\mathrm{lotus}\:\mathrm{plant}\:\mathrm{in}\:\mathrm{a}\:\mathrm{pool}\:\mathrm{of}\:\mathrm{water}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cubit}\:\mathrm{above}\:\mathrm{water}\:\mathrm{level}.\:\mathrm{When} \\ $$$$\mathrm{propelled}\:\mathrm{by}\:\mathrm{air},\:\mathrm{the}\:\mathrm{lotus}\:\mathrm{sinks}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{pool}\:\mathrm{2}\:\mathrm{cubits}\:\mathrm{away}\:\mathrm{from}\:\mathrm{its}\:\mathrm{position}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{depth}\:\mathrm{of}\:\mathrm{water}\:\mathrm{in}\:\mathrm{the}\:\mathrm{pool}. \\ $$

Question Number 17612 Answers: 1 Comments: 2

The accompanying diagram is a road- plan of a city. All the roads go east- west or north-south, with the exception of one shown. Due to repairs one road is impassable at the point X, Of all the possible routes from P to Q, there are several shortest routes. How many such shortest routes are there?

$$\mathrm{The}\:\mathrm{accompanying}\:\mathrm{diagram}\:\mathrm{is}\:\mathrm{a}\:\mathrm{road}- \\ $$$$\mathrm{plan}\:\mathrm{of}\:\mathrm{a}\:\mathrm{city}.\:\mathrm{All}\:\mathrm{the}\:\mathrm{roads}\:\mathrm{go}\:\mathrm{east}- \\ $$$$\mathrm{west}\:\mathrm{or}\:\mathrm{north}-\mathrm{south},\:\mathrm{with}\:\mathrm{the} \\ $$$$\mathrm{exception}\:\mathrm{of}\:\mathrm{one}\:\mathrm{shown}.\:\mathrm{Due}\:\mathrm{to}\:\mathrm{repairs} \\ $$$$\mathrm{one}\:\mathrm{road}\:\mathrm{is}\:\mathrm{impassable}\:\mathrm{at}\:\mathrm{the}\:\mathrm{point}\:\mathrm{X}, \\ $$$$\mathrm{Of}\:\mathrm{all}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{routes}\:\mathrm{from}\:\mathrm{P}\:\mathrm{to}\:\mathrm{Q}, \\ $$$$\mathrm{there}\:\mathrm{are}\:\mathrm{several}\:\mathrm{shortest}\:\mathrm{routes}.\:\mathrm{How} \\ $$$$\mathrm{many}\:\mathrm{such}\:\mathrm{shortest}\:\mathrm{routes}\:\mathrm{are}\:\mathrm{there}? \\ $$

Question Number 17169 Answers: 2 Comments: 0

The base of a pyramid is an equilateral triangle of side length 6 cm. The other edges of the pyramid are each of length (√(15)) cm. Find the volume of the pyramid.

$$\mathrm{The}\:\mathrm{base}\:\mathrm{of}\:\mathrm{a}\:\mathrm{pyramid}\:\mathrm{is}\:\mathrm{an}\:\mathrm{equilateral} \\ $$$$\mathrm{triangle}\:\mathrm{of}\:\mathrm{side}\:\mathrm{length}\:\mathrm{6}\:\mathrm{cm}.\:\mathrm{The}\:\mathrm{other} \\ $$$$\mathrm{edges}\:\mathrm{of}\:\mathrm{the}\:\mathrm{pyramid}\:\mathrm{are}\:\mathrm{each}\:\mathrm{of}\:\mathrm{length} \\ $$$$\sqrt{\mathrm{15}}\:\mathrm{cm}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{volume}\:\mathrm{of}\:\mathrm{the}\:\mathrm{pyramid}. \\ $$

Question Number 16942 Answers: 1 Comments: 0

A distance of 200 km is to be covered by car in less than 10 hours. Yash does it in two parts. He first drives for 150 km at an average speed of 36 km/hr, without stopping. After taking rest for 30 minutes, he starts again and covers the remaining distance non-stop. His average for the entire journey (including the period of rest) exceeds that for the second part by 5 km/hr. Find the speed at which he covers the second part.

$$\mathrm{A}\:\mathrm{distance}\:\mathrm{of}\:\mathrm{200}\:\mathrm{km}\:\mathrm{is}\:\mathrm{to}\:\mathrm{be}\:\mathrm{covered}\:\mathrm{by} \\ $$$$\mathrm{car}\:\mathrm{in}\:\mathrm{less}\:\mathrm{than}\:\mathrm{10}\:\mathrm{hours}.\:\mathrm{Yash}\:\mathrm{does}\:\mathrm{it} \\ $$$$\mathrm{in}\:\mathrm{two}\:\mathrm{parts}.\:\mathrm{He}\:\mathrm{first}\:\mathrm{drives}\:\mathrm{for}\:\mathrm{150}\:\mathrm{km} \\ $$$$\mathrm{at}\:\mathrm{an}\:\mathrm{average}\:\mathrm{speed}\:\mathrm{of}\:\mathrm{36}\:\mathrm{km}/\mathrm{hr}, \\ $$$$\mathrm{without}\:\mathrm{stopping}.\:\mathrm{After}\:\mathrm{taking}\:\mathrm{rest}\:\mathrm{for} \\ $$$$\mathrm{30}\:\mathrm{minutes},\:\mathrm{he}\:\mathrm{starts}\:\mathrm{again}\:\mathrm{and}\:\mathrm{covers} \\ $$$$\mathrm{the}\:\mathrm{remaining}\:\mathrm{distance}\:\mathrm{non}-\mathrm{stop}.\:\mathrm{His} \\ $$$$\mathrm{average}\:\mathrm{for}\:\mathrm{the}\:\mathrm{entire}\:\mathrm{journey} \\ $$$$\left(\mathrm{including}\:\mathrm{the}\:\mathrm{period}\:\mathrm{of}\:\mathrm{rest}\right)\:\mathrm{exceeds} \\ $$$$\mathrm{that}\:\mathrm{for}\:\mathrm{the}\:\mathrm{second}\:\mathrm{part}\:\mathrm{by}\:\mathrm{5}\:\mathrm{km}/\mathrm{hr}. \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{speed}\:\mathrm{at}\:\mathrm{which}\:\mathrm{he}\:\mathrm{covers}\:\mathrm{the} \\ $$$$\mathrm{second}\:\mathrm{part}. \\ $$

Question Number 16938 Answers: 1 Comments: 2

The Object shown in the diagram is made by gluing together the adjacent faces of six wooden cubes, each having edges of length 2 cm. Find the total surface area of the object in square centimetres.

$$\mathrm{The}\:\mathrm{Object}\:\mathrm{shown}\:\mathrm{in}\:\mathrm{the}\:\mathrm{diagram}\:\mathrm{is} \\ $$$$\mathrm{made}\:\mathrm{by}\:\mathrm{gluing}\:\mathrm{together}\:\mathrm{the}\:\mathrm{adjacent} \\ $$$$\mathrm{faces}\:\mathrm{of}\:\mathrm{six}\:\mathrm{wooden}\:\mathrm{cubes},\:\mathrm{each}\:\mathrm{having} \\ $$$$\mathrm{edges}\:\mathrm{of}\:\mathrm{length}\:\mathrm{2}\:\mathrm{cm}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{total} \\ $$$$\mathrm{surface}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{object}\:\mathrm{in}\:\mathrm{square} \\ $$$$\mathrm{centimetres}. \\ $$

Question Number 16936 Answers: 0 Comments: 5

In the diagram, it is possible to travel only along an edge in the direction indicated by the arrow. How many different routes from A to B are there in all?

$$\mathrm{In}\:\mathrm{the}\:\mathrm{diagram},\:\mathrm{it}\:\mathrm{is}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{travel} \\ $$$$\mathrm{only}\:\mathrm{along}\:\mathrm{an}\:\mathrm{edge}\:\mathrm{in}\:\mathrm{the}\:\mathrm{direction} \\ $$$$\mathrm{indicated}\:\mathrm{by}\:\mathrm{the}\:\mathrm{arrow}.\:\mathrm{How}\:\mathrm{many} \\ $$$$\mathrm{different}\:\mathrm{routes}\:\mathrm{from}\:\mathrm{A}\:\mathrm{to}\:\mathrm{B}\:\mathrm{are}\:\mathrm{there} \\ $$$$\mathrm{in}\:\mathrm{all}? \\ $$

Question Number 16701 Answers: 1 Comments: 0

Find distinct natural numbers from 1 to 9 such that these six equations are satisfied simultaneously: (1) a + bc = 20 (2) d + e + f = 20 (3) g − hi = −20 (4) adg = 20 (5) b + eh = 20 (6) c + f − i = 10

$$\mathrm{Find}\:\mathrm{distinct}\:\mathrm{natural}\:\mathrm{numbers}\:\mathrm{from}\:\mathrm{1} \\ $$$$\mathrm{to}\:\mathrm{9}\:\mathrm{such}\:\mathrm{that}\:\mathrm{these}\:\mathrm{six}\:\mathrm{equations}\:\mathrm{are} \\ $$$$\mathrm{satisfied}\:\mathrm{simultaneously}: \\ $$$$\left(\mathrm{1}\right)\:{a}\:+\:{bc}\:=\:\mathrm{20} \\ $$$$\left(\mathrm{2}\right)\:{d}\:+\:{e}\:+\:{f}\:=\:\mathrm{20} \\ $$$$\left(\mathrm{3}\right)\:{g}\:−\:{hi}\:=\:−\mathrm{20} \\ $$$$\left(\mathrm{4}\right)\:{adg}\:=\:\mathrm{20} \\ $$$$\left(\mathrm{5}\right)\:{b}\:+\:{eh}\:=\:\mathrm{20} \\ $$$$\left(\mathrm{6}\right)\:{c}\:+\:{f}\:−\:{i}\:=\:\mathrm{10} \\ $$

Question Number 15601 Answers: 0 Comments: 0

order of a circle whose centre is origin and radius is r .

$$\mathrm{order}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{whose}\:\mathrm{centre}\:\mathrm{is}\: \\ $$$$\mathrm{origin}\:\mathrm{and}\:\mathrm{radius}\:\mathrm{is}\:\mathrm{r}\:. \\ $$

Question Number 15201 Answers: 0 Comments: 0

If z = x + jy , where x and y are real, show that the locus ∣((z − 2)/(z + 1))∣ = 2 is a circle and determine its centre and radius.

$$\mathrm{If}\:\:\mathrm{z}\:=\:\mathrm{x}\:+\:\mathrm{jy}\:,\:\mathrm{where}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{are}\:\mathrm{real},\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{locus}\:\:\mid\frac{\mathrm{z}\:−\:\mathrm{2}}{\mathrm{z}\:+\:\mathrm{1}}\mid\:=\:\mathrm{2}\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{circle} \\ $$$$\mathrm{and}\:\mathrm{determine}\:\mathrm{its}\:\mathrm{centre}\:\mathrm{and}\:\mathrm{radius}. \\ $$

Question Number 13988 Answers: 0 Comments: 3

Question Number 13893 Answers: 0 Comments: 3

Let n be an odd positive integer. On some field, n gunmen are placed such that all pairwise distances between them are different. At a signal, every gunman takes out his gun and shoots the closest gunman. Prove that: (a) at least one gunman survives; (b) no gunman is shot more than 5 times; (c) the trajectories of the bullets do not intersect.

$$\mathrm{Let}\:{n}\:\mathrm{be}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{positive}\:\mathrm{integer}.\:\mathrm{On} \\ $$$$\mathrm{some}\:\mathrm{field},\:{n}\:\mathrm{gunmen}\:\mathrm{are}\:\mathrm{placed}\:\mathrm{such} \\ $$$$\mathrm{that}\:\mathrm{all}\:\mathrm{pairwise}\:\mathrm{distances}\:\mathrm{between} \\ $$$$\mathrm{them}\:\mathrm{are}\:\mathrm{different}.\:\mathrm{At}\:\mathrm{a}\:\mathrm{signal},\:\mathrm{every} \\ $$$$\mathrm{gunman}\:\mathrm{takes}\:\mathrm{out}\:\mathrm{his}\:\mathrm{gun}\:\mathrm{and}\:\mathrm{shoots} \\ $$$$\mathrm{the}\:\mathrm{closest}\:\mathrm{gunman}.\:\mathrm{Prove}\:\mathrm{that}: \\ $$$$\left(\mathrm{a}\right)\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{gunman}\:\mathrm{survives}; \\ $$$$\left(\mathrm{b}\right)\:\mathrm{no}\:\mathrm{gunman}\:\mathrm{is}\:\mathrm{shot}\:\mathrm{more}\:\mathrm{than}\:\mathrm{5} \\ $$$$\mathrm{times}; \\ $$$$\left(\mathrm{c}\right)\:\mathrm{the}\:\mathrm{trajectories}\:\mathrm{of}\:\mathrm{the}\:\mathrm{bullets}\:\mathrm{do} \\ $$$$\mathrm{not}\:\mathrm{intersect}. \\ $$

Question Number 13891 Answers: 0 Comments: 1

Consider n red and n blue points in the plane, no three of them being collinear. Prove that one can connect each red point to a blue one with a segment such that no two segments intersect.

$$\mathrm{Consider}\:{n}\:\mathrm{red}\:\mathrm{and}\:{n}\:\mathrm{blue}\:\mathrm{points}\:\mathrm{in} \\ $$$$\mathrm{the}\:\mathrm{plane},\:\mathrm{no}\:\mathrm{three}\:\mathrm{of}\:\mathrm{them}\:\mathrm{being}\:\mathrm{collinear}. \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{one}\:\mathrm{can}\:\mathrm{connect}\:\mathrm{each}\:\mathrm{red} \\ $$$$\mathrm{point}\:\mathrm{to}\:\mathrm{a}\:\mathrm{blue}\:\mathrm{one}\:\mathrm{with}\:\mathrm{a}\:\mathrm{segment} \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{no}\:\mathrm{two}\:\mathrm{segments}\:\mathrm{intersect}. \\ $$

Pg 1 Pg 2 Pg 3 Pg 4 Pg 5 Pg 6 Pg 7

Contact: info@tinkutara.com