
LogicQuestion and Answers: Page 4
Question Number 93623 Answers: 0 Comments: 2

Question Number 93618 Answers: 0 Comments: 1
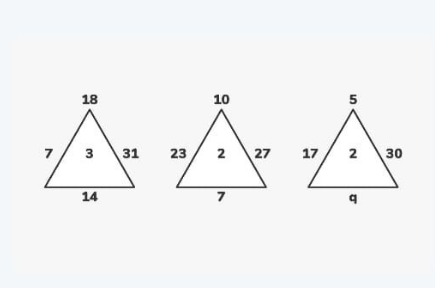
Question Number 92687 Answers: 0 Comments: 0
Question Number 92673 Answers: 1 Comments: 2
Question Number 90801 Answers: 0 Comments: 3
Question Number 90233 Answers: 0 Comments: 5
Question Number 90200 Answers: 0 Comments: 7
Question Number 88943 Answers: 0 Comments: 2
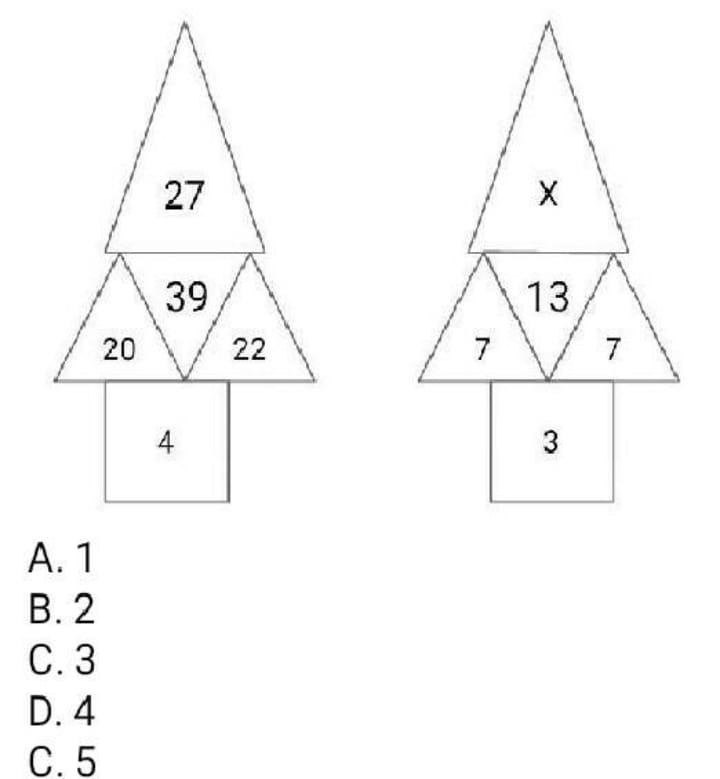
Question Number 88940 Answers: 1 Comments: 0

Question Number 88690 Answers: 1 Comments: 0

Question Number 85555 Answers: 1 Comments: 0
$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{7}=\mathrm{0} \\ $$
Question Number 79462 Answers: 1 Comments: 0
Question Number 78671 Answers: 1 Comments: 0
$${prove}\:{p}\Rightarrow{q}\:{and}\:{negetion}\:{of}\:{q}\Rightarrow{negation}\:{of}\:{p} \\ $$
Question Number 75255 Answers: 0 Comments: 0
Question Number 75254 Answers: 1 Comments: 0
Question Number 75257 Answers: 1 Comments: 0
Question Number 74246 Answers: 2 Comments: 0

Question Number 71849 Answers: 1 Comments: 0
Question Number 70742 Answers: 0 Comments: 1
Question Number 70168 Answers: 1 Comments: 3
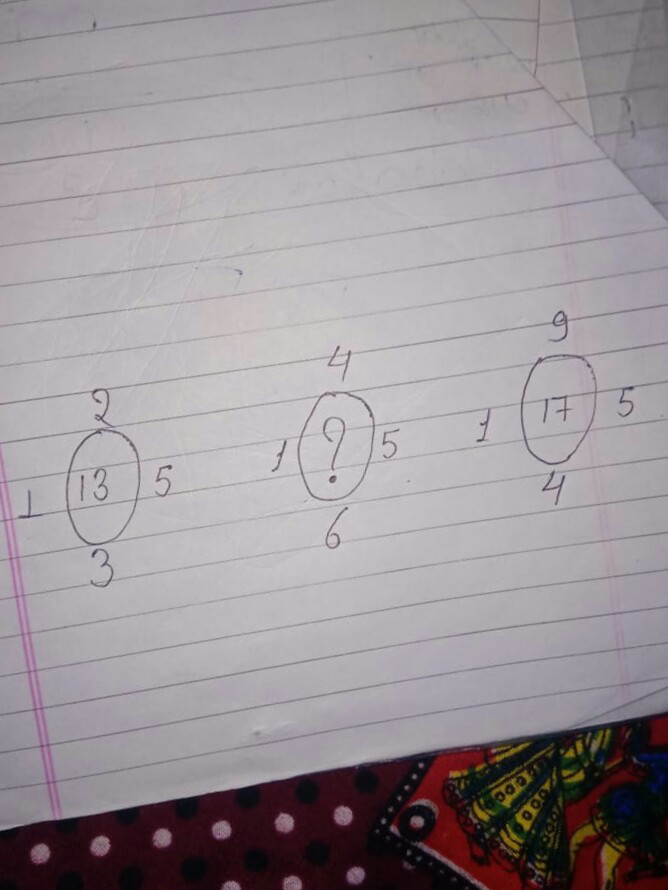
Question Number 69116 Answers: 0 Comments: 0
Question Number 68695 Answers: 1 Comments: 0
Question Number 67651 Answers: 0 Comments: 0
Question Number 65427 Answers: 0 Comments: 1

Question Number 61934 Answers: 1 Comments: 2
Question Number 60484 Answers: 1 Comments: 2
