Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 188984 by normans last updated on 10/Mar/23

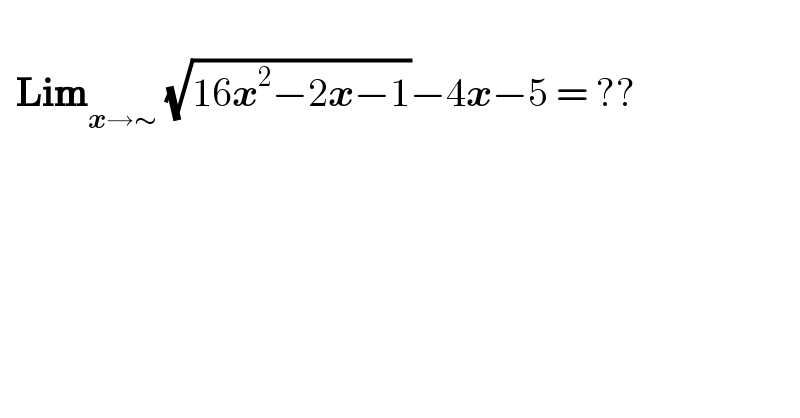
Lim_(x→∼) (√(16x^2 −2x−1))−4x−5 = ??

$$ \\ $$$$\:\:\boldsymbol{\mathrm{Lim}}_{\boldsymbol{{x}}\rightarrow\sim} \:\sqrt{\mathrm{16}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{x}}−\mathrm{1}}−\mathrm{4}\boldsymbol{{x}}−\mathrm{5}\:=\:??\:\:\:\: \\ $$$$ \\ $$

Commented by MJS_new last updated on 13/Mar/23

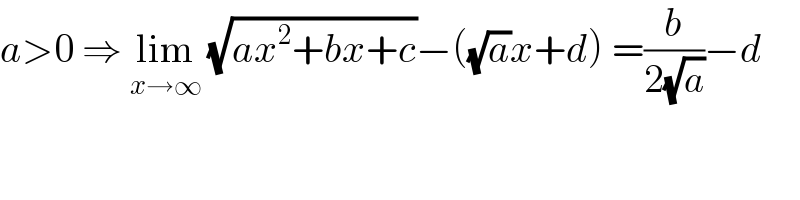
a>0 ⇒ lim_(x→∞) (√(ax^2 +bx+c))−((√a)x+d) =(b/(2(√a)))−d

$${a}>\mathrm{0}\:\Rightarrow\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{{ax}^{\mathrm{2}} +{bx}+{c}}−\left(\sqrt{{a}}{x}+{d}\right)\:=\frac{{b}}{\mathrm{2}\sqrt{{a}}}−{d} \\ $$

Commented by cortano12 last updated on 13/Mar/23

it should be L=(b/(2(√a))) −d

$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{L}=\frac{\mathrm{b}}{\mathrm{2}\sqrt{\mathrm{a}}}\:−\mathrm{d} \\ $$$$ \\ $$

Commented by cortano12 last updated on 13/Mar/23

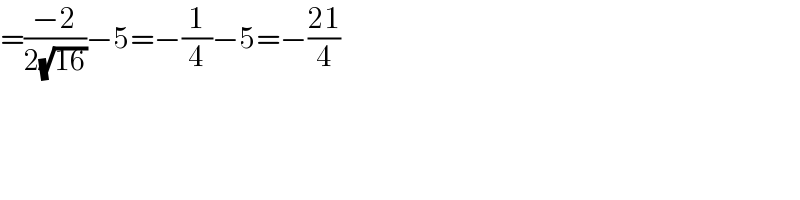
=((−2)/(2(√(16))))−5=−(1/4)−5=−((21)/4)

$$=\frac{−\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{16}}}−\mathrm{5}=−\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{5}=−\frac{\mathrm{21}}{\mathrm{4}} \\ $$

Commented by MJS_new last updated on 13/Mar/23

yes, thank you

$$\mathrm{yes},\:\mathrm{thank}\:\mathrm{you} \\ $$

Answered by cortano12 last updated on 10/Mar/23

lim_(x→∞) (√(16x^2 −2x−1))−4x−5 = lim_(x→∞) 4x [ (√(1−(1/(8x))−(1/(16x^2 ))))−1−(5/(4x)) ] [ (1/(4x)) = h ; h→0 ] = lim_(h→0) (1/h) [ (√(1−(1/2)h−h^2 ))−1−5h ] = −5 + lim_(h→0) (((√(1−(1/2)h−h^2 ))−1)/h) = −5+(1/2) lim_(h→0) ((h(−(1/2)−h))/h) =−((21)/4)

$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{16x}^{\mathrm{2}} −\mathrm{2x}−\mathrm{1}}−\mathrm{4x}−\mathrm{5} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{4x}\:\left[\:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8x}}−\frac{\mathrm{1}}{\mathrm{16x}^{\mathrm{2}} }}−\mathrm{1}−\frac{\mathrm{5}}{\mathrm{4x}}\:\right] \\ $$$$\:\left[\:\frac{\mathrm{1}}{\mathrm{4x}}\:=\:\mathrm{h}\:;\:\mathrm{h}\rightarrow\mathrm{0}\:\right] \\ $$$$=\:\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{h}}\:\left[\:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{h}−\mathrm{h}^{\mathrm{2}} }−\mathrm{1}−\mathrm{5h}\:\right] \\ $$$$=\:−\mathrm{5}\:+\:\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{h}−\mathrm{h}^{\mathrm{2}} }−\mathrm{1}}{\mathrm{h}} \\ $$$$=\:−\mathrm{5}+\frac{\mathrm{1}}{\mathrm{2}}\:\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{h}\left(−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{h}\right)}{\mathrm{h}} \\ $$$$=−\frac{\mathrm{21}}{\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com