
Question Number 49151 by rahul 19 last updated on 03/Dec/18
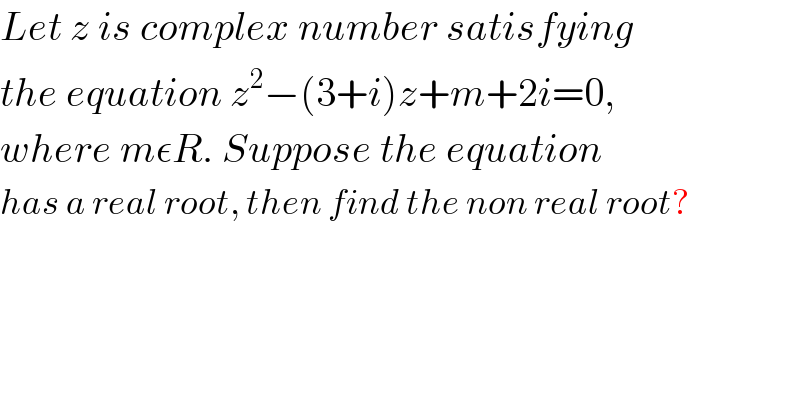
$${Let}\:{z}\:{is}\:{complex}\:{number}\:{satisfying} \\ $$$${the}\:{equation}\:{z}^{\mathrm{2}} −\left(\mathrm{3}+{i}\right){z}+{m}+\mathrm{2}{i}=\mathrm{0}, \\ $$$${where}\:{m}\epsilon{R}.\:{Suppose}\:{the}\:{equation} \\ $$$${has}\:{a}\:{real}\:{root},\:{then}\:{find}\:{the}\:{non}\:{real}\:{root}? \\ $$
Answered by mr W last updated on 03/Dec/18

$${z}_{\mathrm{1}} ={a}={the}\:{real}\:{root} \\ $$$${z}_{\mathrm{2}} ={p}+{qi}={the}\:{non}\:{real}\:{root} \\ $$$${a}+{p}+{qi}=\mathrm{3}+{i} \\ $$$${a}\left({p}+{qi}\right)={m}+\mathrm{2}{i} \\ $$$${q}=\mathrm{1} \\ $$$${a}+{p}=\mathrm{3} \\ $$$${aq}=\mathrm{2}\Rightarrow{a}=\mathrm{2} \\ $$$${ap}={m} \\ $$$$\Rightarrow{p}=\mathrm{1} \\ $$$$\Rightarrow{z}_{\mathrm{2}} =\mathrm{1}+{i} \\ $$$${m}=\mathrm{2} \\ $$
Commented by rahul 19 last updated on 04/Dec/18
thanks sir ����
