Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 19687 by Tinkutara last updated on 14/Aug/17

Let z_1 , z_2 , z_3 be three vertices of an equilateral triangle circumscribing the circle ∣z∣ = (1/2). If z_1 = (1/2) + (((√3)i)/2) and z_1 , z_2 , z_3 are in anticlockwise sense then z_2 is

$$\mathrm{Let}\:{z}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} ,\:{z}_{\mathrm{3}} \:\mathrm{be}\:\mathrm{three}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{an} \\ $$$$\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{circumscribing}\:\mathrm{the} \\ $$$$\mathrm{circle}\:\mid{z}\mid\:=\:\frac{\mathrm{1}}{\mathrm{2}}.\:\mathrm{If}\:{z}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\:\mathrm{and}\:{z}_{\mathrm{1}} , \\ $$$${z}_{\mathrm{2}} ,\:{z}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{in}\:\mathrm{anticlockwise}\:\mathrm{sense}\:\mathrm{then}\:{z}_{\mathrm{2}} \:\mathrm{is} \\ $$

Answered by ajfour last updated on 14/Aug/17

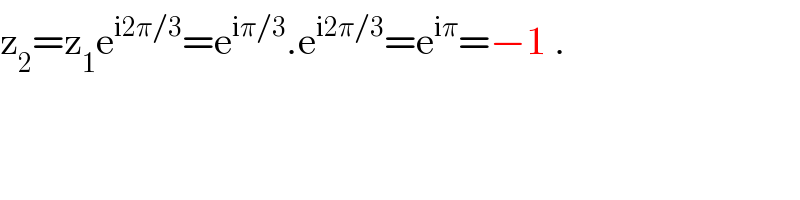
z_2 =z_1 e^(i2π/3) =e^(iπ/3) .e^(i2π/3) =e^(iπ) =−1 .

$$\mathrm{z}_{\mathrm{2}} =\mathrm{z}_{\mathrm{1}} \mathrm{e}^{\mathrm{i2}\pi/\mathrm{3}} =\mathrm{e}^{\mathrm{i}\pi/\mathrm{3}} .\mathrm{e}^{\mathrm{i2}\pi/\mathrm{3}} =\mathrm{e}^{\mathrm{i}\pi} =−\mathrm{1}\:. \\ $$

Commented by Tinkutara last updated on 14/Aug/17

Thank you very much Sir!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com