
Question Number 207194 by sniper237 last updated on 09/May/24
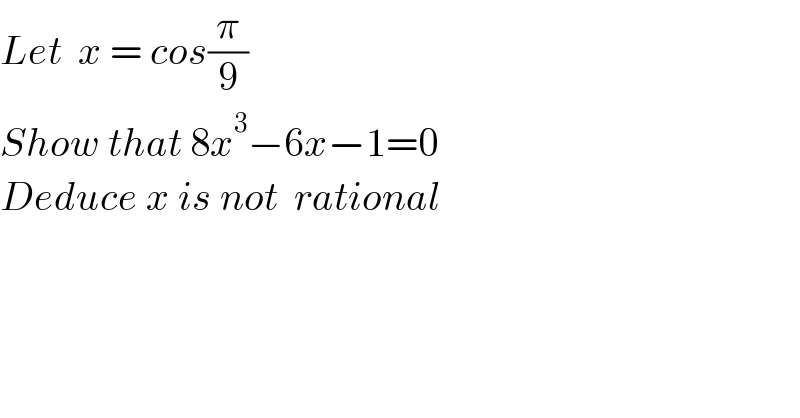
$${Let}\:\:{x}\:=\:{cos}\frac{\pi}{\mathrm{9}}\: \\ $$$${Show}\:{that}\:\mathrm{8}{x}^{\mathrm{3}} −\mathrm{6}{x}−\mathrm{1}=\mathrm{0} \\ $$$${Deduce}\:{x}\:{is}\:{not}\:\:{rational}\: \\ $$
Answered by Berbere last updated on 09/May/24
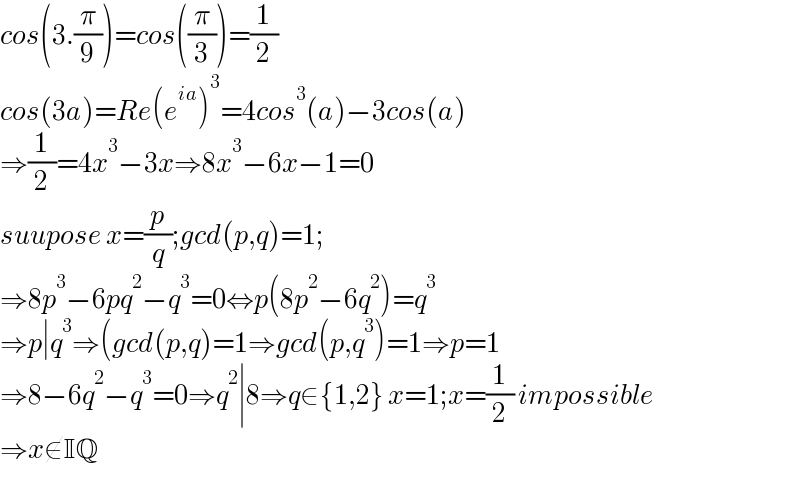
$${cos}\left(\mathrm{3}.\frac{\pi}{\mathrm{9}}\right)={cos}\left(\frac{\pi}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${cos}\left(\mathrm{3}{a}\right)={Re}\left({e}^{{ia}} \right)^{\mathrm{3}} =\mathrm{4}{cos}^{\mathrm{3}} \left({a}\right)−\mathrm{3}{cos}\left({a}\right) \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{4}{x}^{\mathrm{3}} −\mathrm{3}{x}\Rightarrow\mathrm{8}{x}^{\mathrm{3}} −\mathrm{6}{x}−\mathrm{1}=\mathrm{0} \\ $$$${suupose}\:{x}=\frac{{p}}{{q}};{gcd}\left({p},{q}\right)=\mathrm{1}; \\ $$$$\Rightarrow\mathrm{8}{p}^{\mathrm{3}} −\mathrm{6}{pq}^{\mathrm{2}} −{q}^{\mathrm{3}} =\mathrm{0}\Leftrightarrow{p}\left(\mathrm{8}{p}^{\mathrm{2}} −\mathrm{6}{q}^{\mathrm{2}} \right)={q}^{\mathrm{3}} \\ $$$$\Rightarrow{p}\mid{q}^{\mathrm{3}} \Rightarrow\left({gcd}\left({p},{q}\right)=\mathrm{1}\Rightarrow{gcd}\left({p},{q}^{\mathrm{3}} \right)=\mathrm{1}\Rightarrow{p}=\mathrm{1}\right. \\ $$$$\Rightarrow\mathrm{8}−\mathrm{6}{q}^{\mathrm{2}} −{q}^{\mathrm{3}} =\mathrm{0}\Rightarrow{q}^{\mathrm{2}} \mid\mathrm{8}\Rightarrow{q}\in\left\{\mathrm{1},\mathrm{2}\right\}\:{x}=\mathrm{1};{x}=\frac{\mathrm{1}}{\mathrm{2}}\:{impossible} \\ $$$$\Rightarrow{x}\notin\mathbb{IQ} \\ $$
