
Question Number 216875 by ArshadS last updated on 23/Feb/25
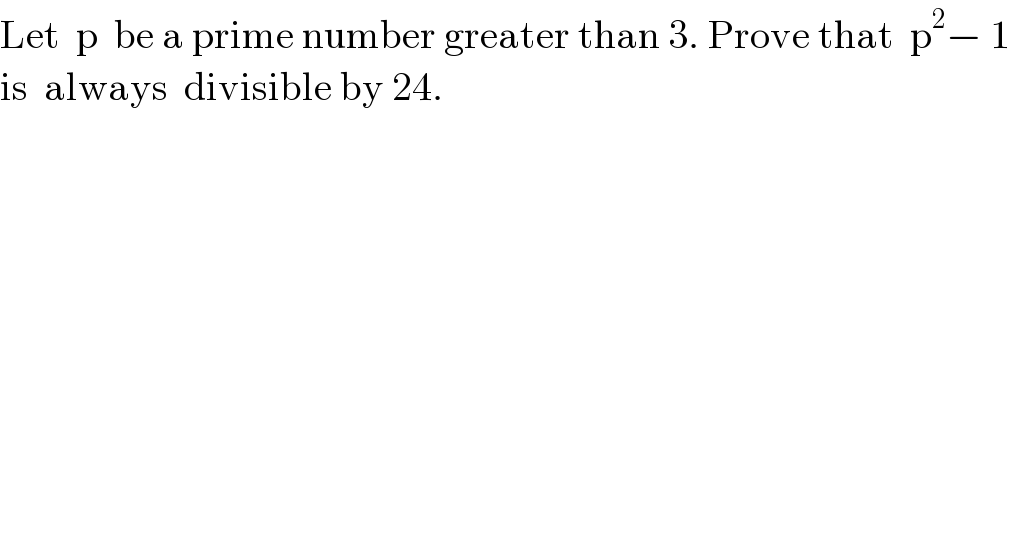
$$\mathrm{Let}\:\:\mathrm{p}\:\:\mathrm{be}\:\mathrm{a}\:\mathrm{prime}\:\mathrm{number}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{3}.\:\mathrm{Prove}\:\mathrm{that}\:\:\mathrm{p}^{\mathrm{2}} −\:\mathrm{1}\:\: \\ $$$$\mathrm{is}\:\:\mathrm{always}\:\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{24}. \\ $$
Answered by maths2 last updated on 23/Feb/25
![(p−1)(p+1) 3∣(p−1)(p+1);since p≡1,2[3] p≡1,3,5,7[8] ⇒p^2 ≡1[8]⇒8∣p^2 −1 since 3 and 8 are coprim 3.8=24∣p^2 −1](Q216877.png)
$$\left({p}−\mathrm{1}\right)\left({p}+\mathrm{1}\right) \\ $$$$\mathrm{3}\mid\left({p}−\mathrm{1}\right)\left({p}+\mathrm{1}\right);{since}\:{p}\equiv\mathrm{1},\mathrm{2}\left[\mathrm{3}\right] \\ $$$${p}\equiv\mathrm{1},\mathrm{3},\mathrm{5},\mathrm{7}\left[\mathrm{8}\right] \\ $$$$\Rightarrow{p}^{\mathrm{2}} \equiv\mathrm{1}\left[\mathrm{8}\right]\Rightarrow\mathrm{8}\mid{p}^{\mathrm{2}} −\mathrm{1} \\ $$$${since}\:\mathrm{3}\:{and}\:\mathrm{8}\:{are}\:{coprim}\:\mathrm{3}.\mathrm{8}=\mathrm{24}\mid{p}^{\mathrm{2}} −\mathrm{1} \\ $$
Commented by ArshadS last updated on 23/Feb/25
$$\mathcal{N}{ice}!\:\mathcal{T}{hanks}\:{sir}! \\ $$
