
Question Number 209881 by naka3546 last updated on 24/Jul/24
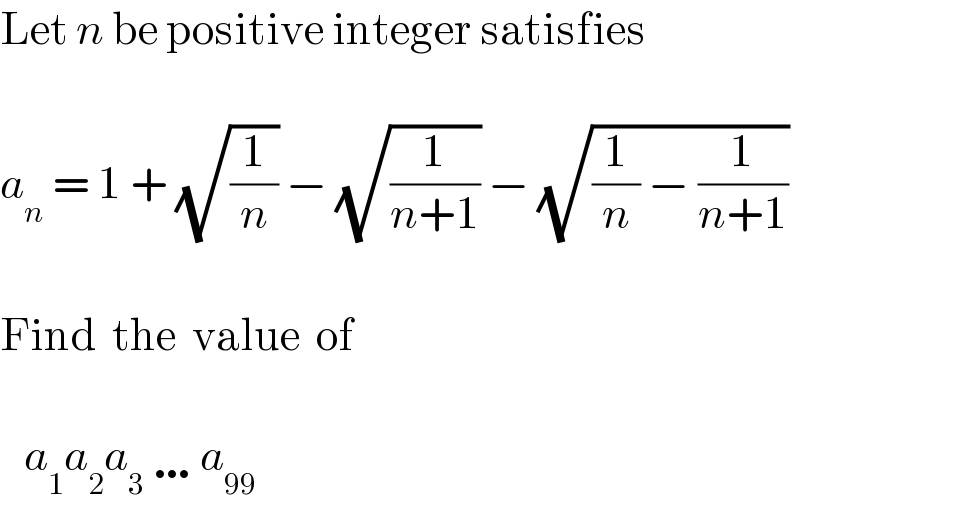
$$\mathrm{Let}\:{n}\:\mathrm{be}\:\mathrm{positive}\:\mathrm{integer}\:\mathrm{satisfies} \\ $$$$ \\ $$$${a}_{{n}} \:=\:\mathrm{1}\:+\:\sqrt{\frac{\mathrm{1}}{{n}}}\:−\:\sqrt{\frac{\mathrm{1}}{{n}+\mathrm{1}}}\:−\:\sqrt{\frac{\mathrm{1}}{{n}}\:−\:\frac{\mathrm{1}}{{n}+\mathrm{1}}} \\ $$$$ \\ $$$$\mathrm{Find}\:\:\mathrm{the}\:\:\mathrm{value}\:\:\mathrm{of}\: \\ $$$$ \\ $$$$\:\:\:{a}_{\mathrm{1}} {a}_{\mathrm{2}} {a}_{\mathrm{3}} \:\ldots{a}_{\mathrm{99}} \\ $$
Commented by Frix last updated on 24/Jul/24
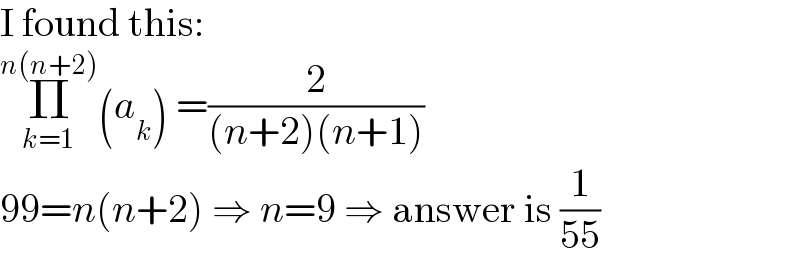
$$\mathrm{I}\:\mathrm{found}\:\mathrm{this}: \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}\left({n}+\mathrm{2}\right)} {\prod}}\left({a}_{{k}} \right)\:=\frac{\mathrm{2}}{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right)} \\ $$$$\mathrm{99}={n}\left({n}+\mathrm{2}\right)\:\Rightarrow\:{n}=\mathrm{9}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{55}} \\ $$
Commented by naka3546 last updated on 24/Jul/24

$$\mathrm{Thanks} \\ $$
