
Question Number 215760 by MATHEMATICSAM last updated on 17/Jan/25
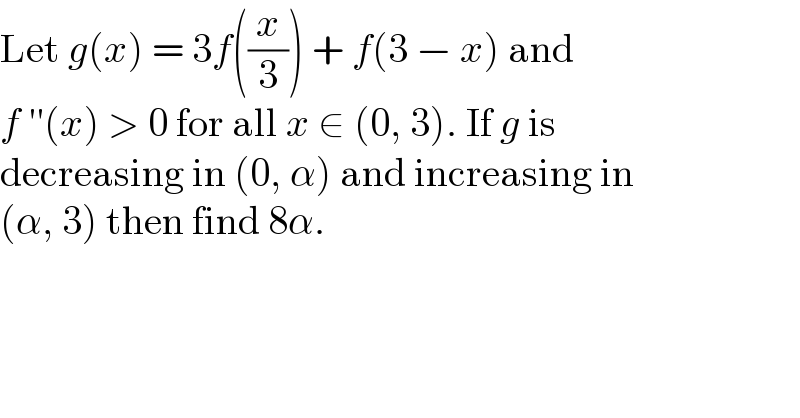
$$\mathrm{Let}\:{g}\left({x}\right)\:=\:\mathrm{3}{f}\left(\frac{{x}}{\mathrm{3}}\right)\:+\:{f}\left(\mathrm{3}\:−\:{x}\right)\:\mathrm{and}\: \\ $$$${f}\:''\left({x}\right)\:>\:\mathrm{0}\:\mathrm{for}\:\mathrm{all}\:{x}\:\in\:\left(\mathrm{0},\:\mathrm{3}\right).\:\mathrm{If}\:{g}\:\mathrm{is}\: \\ $$$$\mathrm{decreasing}\:\mathrm{in}\:\left(\mathrm{0},\:\alpha\right)\:\mathrm{and}\:\mathrm{increasing}\:\mathrm{in} \\ $$$$\left(\alpha,\:\mathrm{3}\right)\:\mathrm{then}\:\mathrm{find}\:\mathrm{8}\alpha. \\ $$
Answered by universe last updated on 18/Jan/25

$${f}''\left({x}\right)>\mathrm{0}=>{f}'\:{is}\:{strictly}\:{increasing}\: \\ $$$${g}'\left({x}\right)={f}'\left({x}/\mathrm{3}\right)−{f}'\left(\mathrm{3}−{x}\right) \\ $$$${g}'\left({x}\right)=\mathrm{0} \\ $$$$\frac{{x}}{\mathrm{3}}\:=\:\mathrm{3}−{x} \\ $$$${x}+{x}/\mathrm{3}=\:\mathrm{3} \\ $$$$\:{x}\:=\:\frac{\mathrm{9}}{\mathrm{4}}\:{is}\:{a}\:{critical}\:{point} \\ $$$${g}\left({x}\right)\:{is}\:{decreing}\:\left(\mathrm{0},\mathrm{9}/\mathrm{4}\right) \\ $$$$\:\alpha\:=\mathrm{9}/\mathrm{4} \\ $$$$\mathrm{8}\alpha\:=\:\mathrm{18} \\ $$$$ \\ $$
Commented by MATHEMATICSAM last updated on 17/Jan/25

$$\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{given}\:\mathrm{18} \\ $$
