Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 53212 by Joel578 last updated on 19/Jan/19

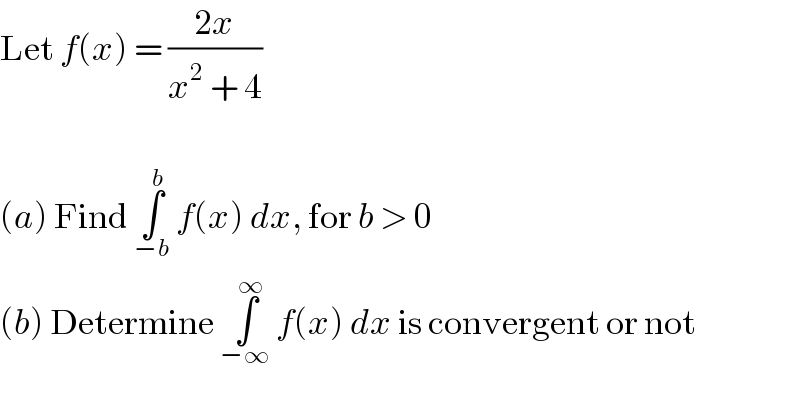
Let f(x) = ((2x)/(x^2 + 4)) (a) Find ∫_(−b) ^b f(x) dx, for b > 0 (b) Determine ∫_(−∞) ^∞ f(x) dx is convergent or not

$$\mathrm{Let}\:{f}\left({x}\right)\:=\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\:\mathrm{4}} \\ $$ $$ \\ $$ $$\left({a}\right)\:\mathrm{Find}\:\underset{−{b}} {\overset{{b}} {\int}}\:{f}\left({x}\right)\:{dx},\:\mathrm{for}\:{b}\:>\:\mathrm{0} \\ $$ $$\left({b}\right)\:\mathrm{Determine}\:\underset{−\infty} {\overset{\infty} {\int}}\:{f}\left({x}\right)\:{dx}\:\mathrm{is}\:\mathrm{convergent}\:\mathrm{or}\:\mathrm{not} \\ $$

Commented byJoel578 last updated on 19/Jan/19

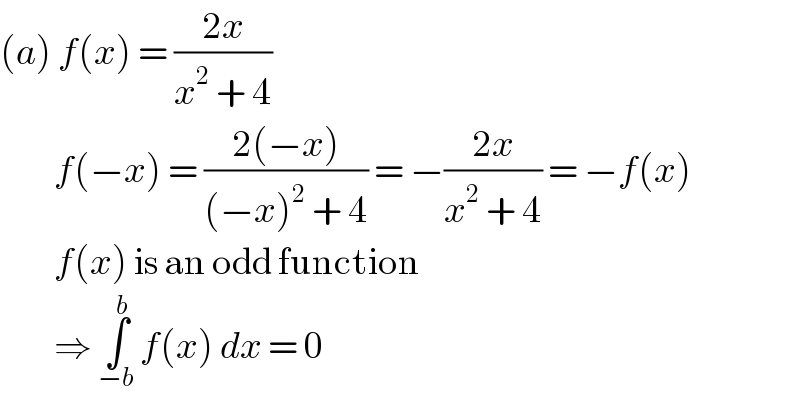
(a) f(x) = ((2x)/(x^2 + 4)) f(−x) = ((2(−x))/((−x)^2 + 4)) = −((2x)/(x^2 + 4)) = −f(x) f(x) is an odd function ⇒ ∫_(−b) ^b f(x) dx = 0

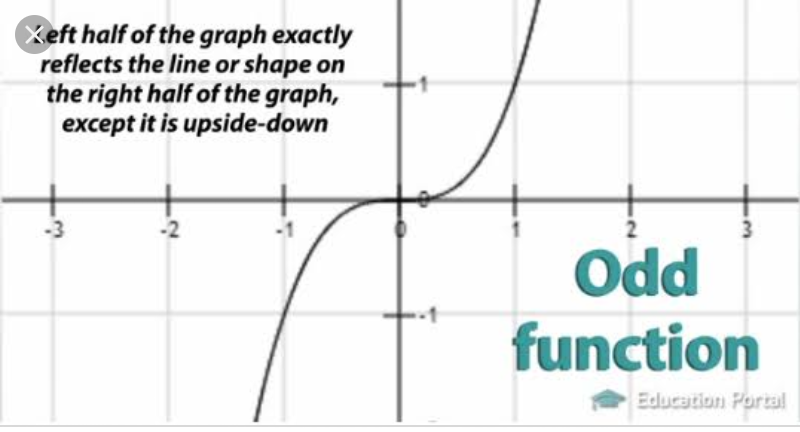
$$\left({a}\right)\:{f}\left({x}\right)\:=\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\:\mathrm{4}} \\ $$ $$\:\:\:\:\:\:\:\:\:{f}\left(−{x}\right)\:=\:\frac{\mathrm{2}\left(−{x}\right)}{\left(−{x}\right)^{\mathrm{2}} \:+\:\mathrm{4}}\:=\:−\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+\:\mathrm{4}}\:=\:−{f}\left({x}\right) \\ $$ $$\:\:\:\:\:\:\:\:\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{an}\:\mathrm{odd}\:\mathrm{function} \\ $$ $$\:\:\:\:\:\:\:\:\:\Rightarrow\:\underset{−{b}} {\overset{{b}} {\int}}\:{f}\left({x}\right)\:{dx}\:=\:\mathrm{0} \\ $$

Commented byJoel578 last updated on 19/Jan/19

Please help with part (b)

$$\mathrm{Please}\:\mathrm{help}\:\mathrm{with}\:\mathrm{part}\:\left({b}\right) \\ $$

Commented bytanmay.chaudhury50@gmail.com last updated on 19/Jan/19

1.((2x)/(x^2 +4)) is odd function because f(−x)=−f(x) 2.the intregal ∫_(−b) ^b ((2x)/(x^2 +4))dx=∫_(−b) ^0 ((2x)/(x^2 +4))dx+∫_0 ^b ((2x)/(x^2 +4))dx I=I_1 +I_2 though I_1 =I_2 but I_1 represent area bound by curve ((2x)/(4+x^2 )) from x=−b to x=0 but that area is below x axis so negetive area . I_2 represent the area bound by the curve ((2x)/(4+x^2 )) from x=0 to x=b above x axis so +ve area hence I_1 +I_2 =0 this is my opinion let others comment...

$$\mathrm{1}.\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}\:{is}\:{odd}\:{function}\:\:{because}\:{f}\left(−{x}\right)=−{f}\left({x}\right) \\ $$ $$\mathrm{2}.{the}\:{intregal}\:\int_{−{b}} ^{{b}} \frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}=\int_{−{b}} ^{\mathrm{0}} \frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}+\int_{\mathrm{0}} ^{{b}} \frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx} \\ $$ $${I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} \\ $$ $${though}\:{I}_{\mathrm{1}} ={I}_{\mathrm{2}} \:{but}\:{I}_{\mathrm{1}} {represent}\:{area}\:{bound}\:{by} \\ $$ $${curve}\:\frac{\mathrm{2}{x}}{\mathrm{4}+{x}^{\mathrm{2}} }\:\:{from}\:\:{x}=−{b}\:\:{to}\:{x}=\mathrm{0}\:\:{but}\:{that}\:{area} \\ $$ $${is}\:{below}\:{x}\:{axis}\:{so}\:\:{negetive}\:{area}\:. \\ $$ $${I}_{\mathrm{2}} \:{represent}\:{the}\:{area}\:{bound}\:{by}\:{the}\:{curve}\:\frac{\mathrm{2}{x}}{\mathrm{4}+{x}^{\mathrm{2}} } \\ $$ $${from}\:{x}=\mathrm{0}\:\:{to}\:{x}={b}\:\:{above}\:{x}\:{axis}\:{so}\:+{ve}\:{area} \\ $$ $${hence}\:{I}_{\mathrm{1}} +{I}_{\mathrm{2}} =\mathrm{0} \\ $$ $${this}\:{is}\:{my}\:{opinion}\:{let}\:{others}\:{comment}... \\ $$ $$ \\ $$ $$ \\ $$

Commented byafachri last updated on 19/Jan/19

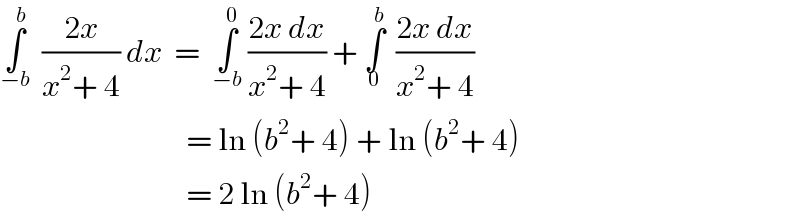
∫_(−b) ^b ((2x)/(x^2 + 4)) dx = ∫_(−b) ^0 ((2x dx)/(x^2 + 4)) + ∫_0 ^b ((2x dx)/(x^2 + 4)) = ln (b^2 + 4) + ln (b^2 + 4) = 2 ln (b^2 + 4)

$$\underset{−{b}} {\overset{{b}} {\int}}\:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:{dx}\:\:=\:\:\underset{−{b}} {\overset{\mathrm{0}} {\int}}\:\frac{\mathrm{2}{x}\:{dx}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:+\:\underset{\mathrm{0}} {\overset{{b}} {\int}}\:\:\frac{\mathrm{2}{x}\:{dx}}{{x}^{\mathrm{2}} +\:\mathrm{4}} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{ln}\:\left({b}^{\mathrm{2}} +\:\mathrm{4}\right)\:+\:\mathrm{ln}\:\left({b}^{\mathrm{2}} +\:\mathrm{4}\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\:\mathrm{ln}\:\left({b}^{\mathrm{2}} +\:\mathrm{4}\right) \\ $$

Commented byafachri last updated on 19/Jan/19

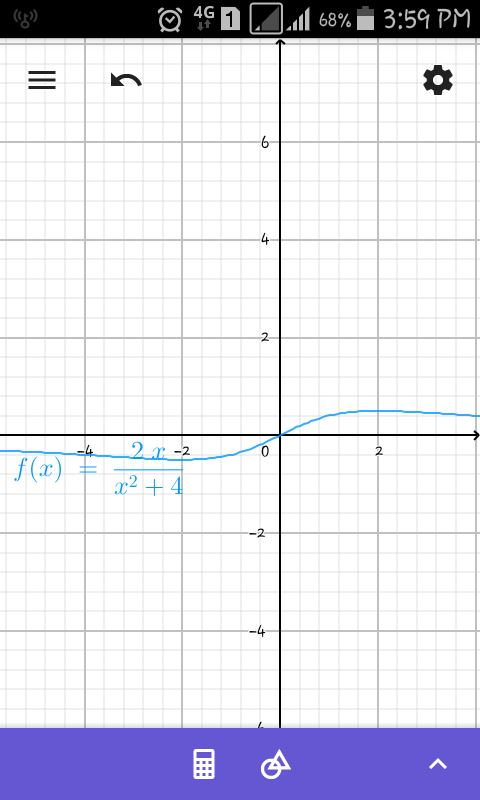
Commented byafachri last updated on 19/Jan/19

in my opinion to the part B, we can define ∫_(−∞) ^∞ f(x) is convergent or not by check the limit. it′s divergent while lim_(x→∞) f(x) = ∞. lim_(x→∞) ((2x)/(x^2 + 4)) = lim_(x→∞) ((x^2 ((2/x)))/(x^2 (1 + (4/x^2 )))) = lim_(x→∞) (0/(1 + 0)) = 0 f(x) = ((2x)/(x^2 + 4)) converges so ∫_(−∞) ^∞ f(x) does.

$$\mathrm{in}\:\mathrm{my}\:\mathrm{opinion}\:\mathrm{to}\:\mathrm{the}\:\mathrm{part}\:\mathrm{B},\:\mathrm{we}\:\mathrm{can}\:\mathrm{define} \\ $$ $$\underset{−\infty} {\overset{\infty} {\int}}{f}\left({x}\right)\:\mathrm{is}\:\mathrm{convergent}\:\mathrm{or}\:\mathrm{not}\:\mathrm{by}\:\mathrm{check}\:\mathrm{the} \\ $$ $$\mathrm{limit}.\:\mathrm{it}'\mathrm{s}\:\mathrm{divergent}\:\mathrm{while}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{f}\left({x}\right)\:=\:\infty. \\ $$ $$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\frac{{x}^{\mathrm{2}} \left(\frac{\mathrm{2}}{{x}}\right)}{{x}^{\mathrm{2}} \left(\mathrm{1}\:+\:\frac{\mathrm{4}}{{x}^{\mathrm{2}} }\right)} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\:\frac{\mathrm{0}}{\mathrm{1}\:+\:\mathrm{0}} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{0} \\ $$ $${f}\left({x}\right)\:=\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:\:\:\mathrm{converges}\:\mathrm{so}\:\underset{−\infty} {\overset{\infty} {\int}}{f}\left({x}\right)\:\mathrm{does}. \\ $$

Commented byafachri last updated on 19/Jan/19

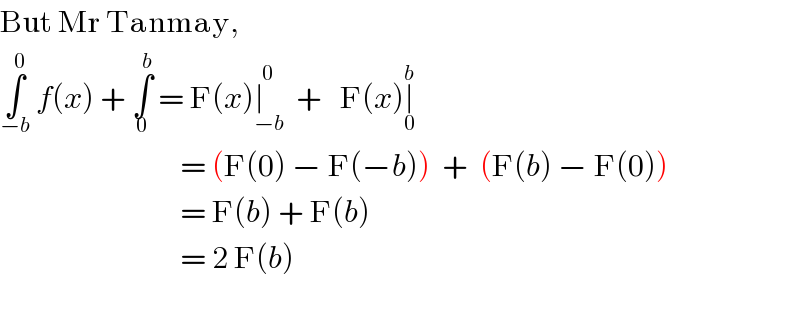
But Mr Tanmay, ∫_(−b) ^0 f(x) + ∫_0 ^b = F(x)∣_(−b) ^0 + F(x)∣_0 ^b = (F(0) − F(−b)) + (F(b) − F(0)) = F(b) + F(b) = 2 F(b)

$$\mathrm{But}\:\mathrm{Mr}\:\mathrm{Tanmay},\: \\ $$ $$\underset{−{b}} {\overset{\mathrm{0}} {\int}}\:{f}\left({x}\right)\:+\:\underset{\mathrm{0}} {\overset{{b}} {\int}}\:=\:\mathrm{F}\left({x}\right)\underset{−{b}} {\overset{\mathrm{0}} {\mid}}\:\:+\:\:\:\mathrm{F}\left({x}\right)\underset{\mathrm{0}} {\overset{{b}} {\mid}} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{F}\left(\mathrm{0}\right)\:−\:\mathrm{F}\left(−{b}\right)\right)\:\:+\:\:\left(\mathrm{F}\left({b}\right)\:−\:\mathrm{F}\left(\mathrm{0}\right)\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{F}\left({b}\right)\:+\:\mathrm{F}\left({b}\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\:\mathrm{F}\left({b}\right) \\ $$ $$ \\ $$

Commented bytanmay.chaudhury50@gmail.com last updated on 19/Jan/19

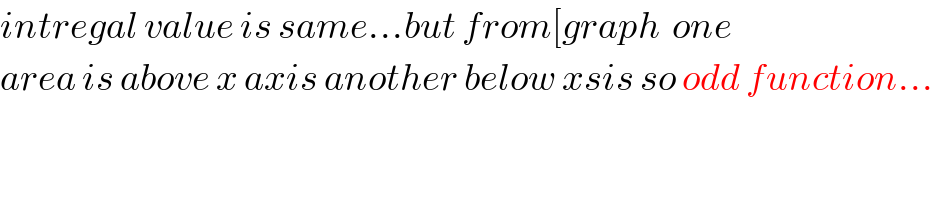
intregal value is same...but from[graph one area is above x axis another below xsis so odd function...

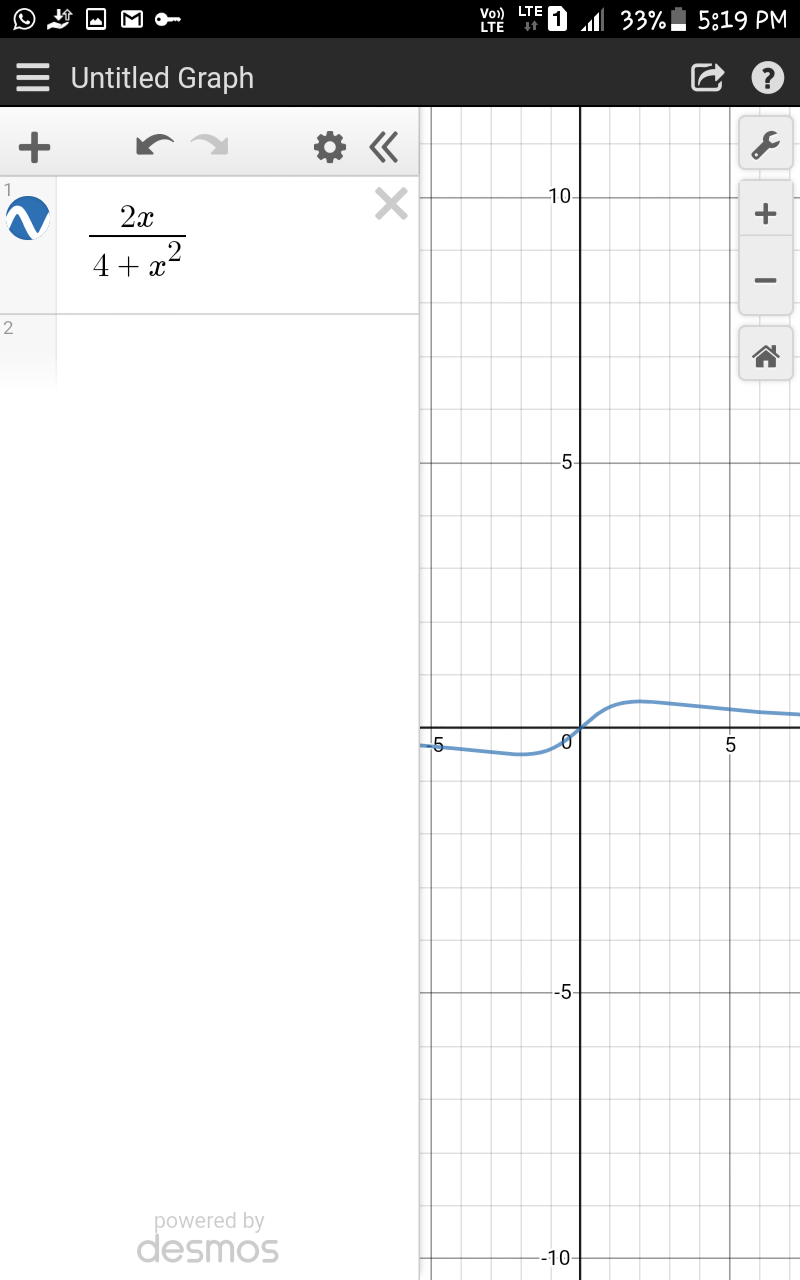
$${intregal}\:{value}\:{is}\:{same}...{but}\:{from}\left[{graph}\:\:{one}\right. \\ $$ $${area}\:{is}\:{above}\:{x}\:{axis}\:{another}\:{below}\:{xsis}\:{so}\:{odd}\:{function}... \\ $$

Commented bytanmay.chaudhury50@gmail.com last updated on 19/Jan/19

Commented bytanmay.chaudhury50@gmail.com last updated on 19/Jan/19

Commented bytanmay.chaudhury50@gmail.com last updated on 19/Jan/19

Commented bytanmay.chaudhury50@gmail.com last updated on 19/Jan/19

Commented byafachri last updated on 19/Jan/19

thank you Mr Damian and all of you Sir who have corrected me for my mistake. what an interesting forum here. now i′m understand it.

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Mr}\:\mathrm{Damian}\:\mathrm{and}\:\mathrm{all}\:\mathrm{of}\:\mathrm{you}\:\mathrm{Sir} \\ $$ $$\mathrm{who}\:\mathrm{have}\:\mathrm{corrected}\:\mathrm{me}\:\mathrm{for}\:\mathrm{my}\:\mathrm{mistake}.\: \\ $$ $$\mathrm{what}\:\mathrm{an}\:\mathrm{interesting}\:\mathrm{forum}\:\mathrm{here}.\:\mathrm{now}\:\mathrm{i}'\mathrm{m} \\ $$ $$\mathrm{understand}\:\mathrm{it}. \\ $$

Commented byafachri last updated on 19/Jan/19

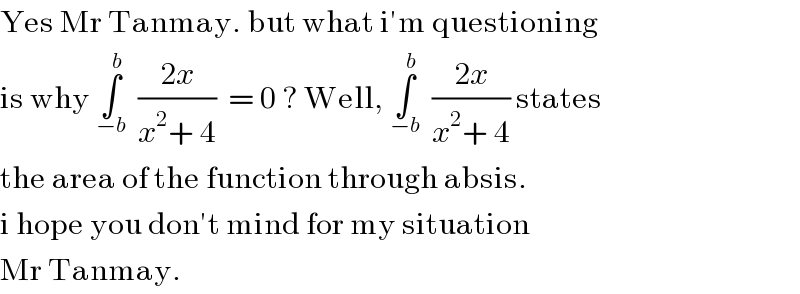
Yes Mr Tanmay. but what i′m questioning is why ∫_(−b) ^b ((2x)/(x^2 + 4)) = 0 ? Well, ∫_(−b) ^b ((2x)/(x^2 + 4)) states the area of the function through absis. i hope you don′t mind for my situation Mr Tanmay.

$$\mathrm{Yes}\:\mathrm{Mr}\:\mathrm{Tanmay}.\:\mathrm{but}\:\mathrm{what}\:\mathrm{i}'\mathrm{m}\:\mathrm{questioning} \\ $$ $$\mathrm{is}\:\mathrm{why}\:\underset{−{b}} {\overset{{b}} {\int}}\:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:\:=\:\mathrm{0}\:?\:\mathrm{Well},\:\underset{−{b}} {\overset{{b}} {\int}}\:\:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\:\mathrm{4}}\:\mathrm{states} \\ $$ $$\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mathrm{through}\:\mathrm{absis}.\: \\ $$ $$\mathrm{i}\:\mathrm{hope}\:\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{mind}\:\mathrm{for}\:\mathrm{my}\:\mathrm{situation}\: \\ $$ $$\mathrm{Mr}\:\mathrm{Tanmay}. \\ $$

Commented bytanmay.chaudhury50@gmail.com last updated on 19/Jan/19

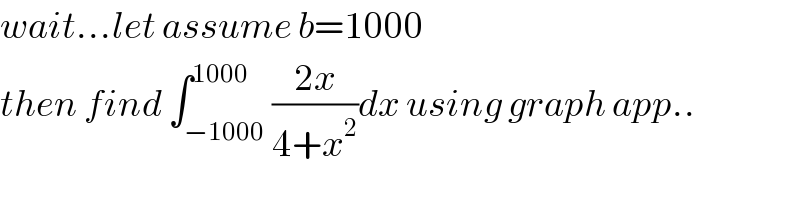
wait...let assume b=1000 then find ∫_(−1000) ^(1000) ((2x)/(4+x^2 ))dx using graph app..

$${wait}...{let}\:{assume}\:{b}=\mathrm{1000} \\ $$ $${then}\:{find}\:\int_{−\mathrm{1000}} ^{\mathrm{1000}} \frac{\mathrm{2}{x}}{\mathrm{4}+{x}^{\mathrm{2}} }{dx}\:{using}\:{graph}\:{app}.. \\ $$

Commented bytanmay.chaudhury50@gmail.com last updated on 19/Jan/19

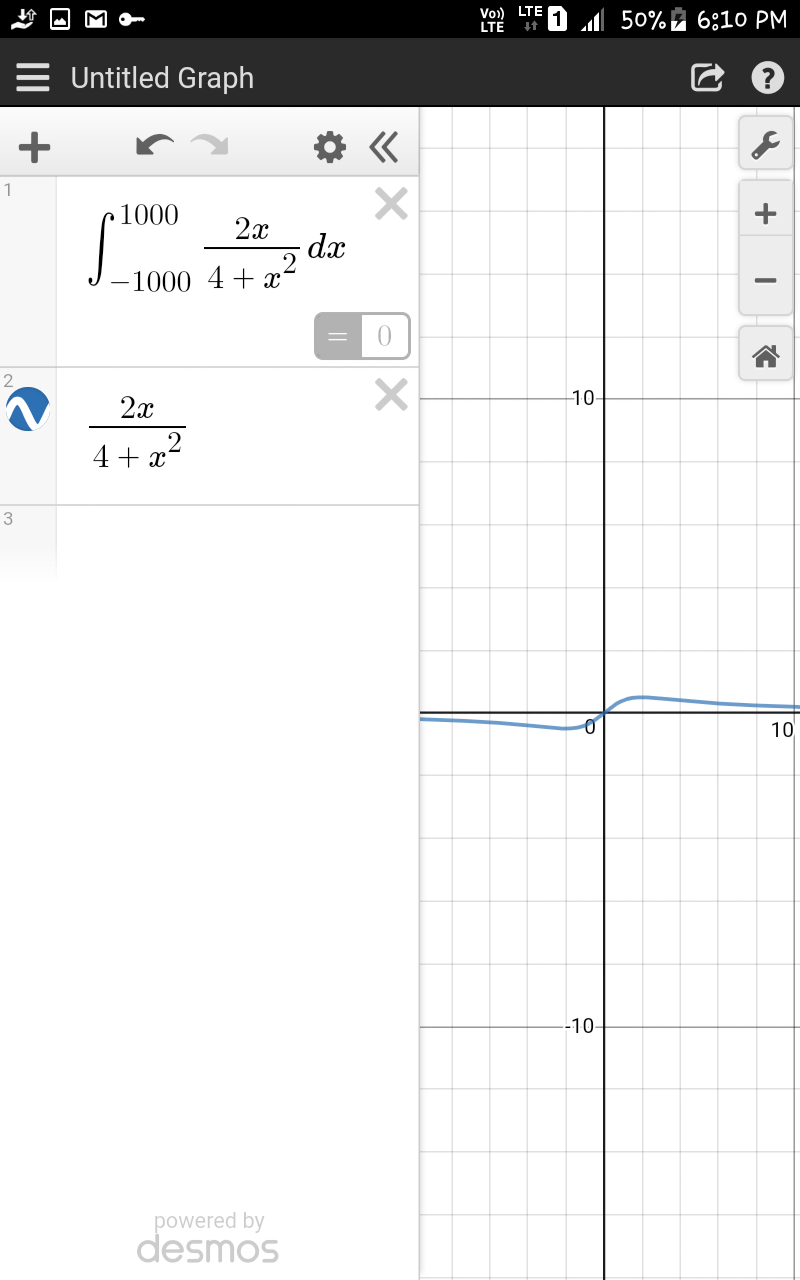
Commented byafachri last updated on 19/Jan/19

Yes Mr Tanmay. Done. Thank You so much. Really appreciate your time Mr Tanmay

$$\mathrm{Yes}\:\mathrm{Mr}\:\mathrm{Tanmay}.\:\mathrm{Done}.\:\mathrm{Thank}\:\mathrm{You} \\ $$ $$\mathrm{so}\:\mathrm{much}.\:\mathrm{Really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$ $$\mathrm{Mr}\:\mathrm{Tanmay} \\ $$

Commented byafachri last updated on 19/Jan/19

Commented byJDamian last updated on 19/Jan/19

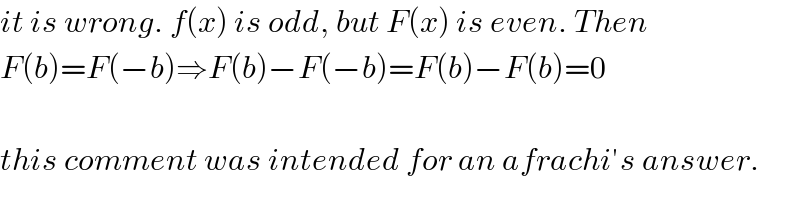
it is wrong. f(x) is odd, but F(x) is even. Then F(b)=F(−b)⇒F(b)−F(−b)=F(b)−F(b)=0 this comment was intended for an afrachi′s answer.

$${it}\:{is}\:{wrong}.\:{f}\left({x}\right)\:{is}\:{odd},\:{but}\:{F}\left({x}\right)\:{is}\:{even}.\:{Then} \\ $$ $${F}\left({b}\right)={F}\left(−{b}\right)\Rightarrow{F}\left({b}\right)−{F}\left(−{b}\right)={F}\left({b}\right)−{F}\left({b}\right)=\mathrm{0} \\ $$ $$ \\ $$ $${this}\:{comment}\:{was}\:{intended}\:{for}\:{an}\:{afrachi}'{s}\:{answer}. \\ $$

Commented byJoel578 last updated on 20/Jan/19

Thanks you Sir afachri, tanmay, JDamian for the answers. Actually I′m agree with Sir tanmay. That′s what I have been taught in Calculus 1. There is a difference between a definite integral and a definite integral as an area

$$\mathrm{Thanks}\:\mathrm{you}\:\mathrm{Sir}\:\mathrm{afachri},\:\mathrm{tanmay},\:\mathrm{JDamian}\:\mathrm{for}\:\mathrm{the}\:\mathrm{answers}. \\ $$ $$\mathrm{Actually}\:\mathrm{I}'\mathrm{m}\:\mathrm{agree}\:\mathrm{with}\:\mathrm{Sir}\:\mathrm{tanmay}.\:\mathrm{That}'\mathrm{s}\: \\ $$ $$\mathrm{what}\:\mathrm{I}\:\mathrm{have}\:\mathrm{been}\:\mathrm{taught}\:\mathrm{in}\:\mathrm{Calculus}\:\mathrm{1}. \\ $$ $$\mathrm{There}\:\mathrm{is}\:\mathrm{a}\:\mathrm{difference}\:\mathrm{between}\:\mathrm{a}\:\mathrm{definite}\:\mathrm{integral} \\ $$ $$\mathrm{and}\:\mathrm{a}\:\mathrm{definite}\:\mathrm{integral}\:\mathrm{as}\:\mathrm{an}\:\mathrm{area} \\ $$

Commented bymaxmathsup by imad last updated on 23/Jan/19

for all odd function integrable on ]−a,a[ a∈R^− we have ∫_(−a) ^a f(x)dx =0.

$$\left.{for}\:{all}\:\:{odd}\:{function}\:\:{integrable}\:{on}\:\right]−{a},{a}\left[\:{a}\in\overset{−} {{R}}\:\:\:{we}\:{have}\:\right. \\ $$ $$\int_{−{a}} ^{{a}} {f}\left({x}\right){dx}\:=\mathrm{0}. \\ $$

Answered by MJS last updated on 20/Jan/19

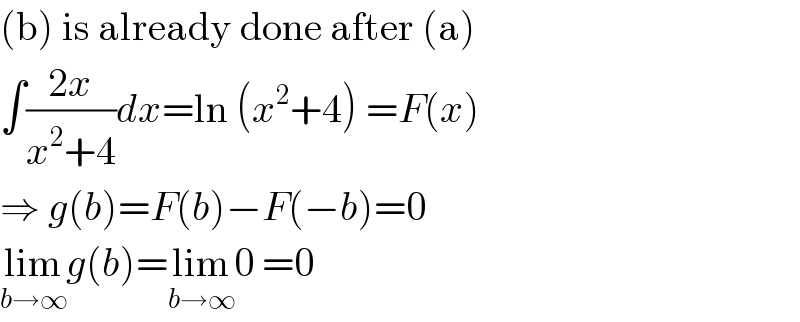
(b) is already done after (a) ∫((2x)/(x^2 +4))dx=ln (x^2 +4) =F(x) ⇒ g(b)=F(b)−F(−b)=0 lim_(b→∞) g(b)=lim_(b→∞) 0 =0

$$\left(\mathrm{b}\right)\:\mathrm{is}\:\mathrm{already}\:\mathrm{done}\:\mathrm{after}\:\left(\mathrm{a}\right) \\ $$ $$\int\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}=\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{4}\right)\:={F}\left({x}\right) \\ $$ $$\Rightarrow\:{g}\left({b}\right)={F}\left({b}\right)−{F}\left(−{b}\right)=\mathrm{0} \\ $$ $$\underset{{b}\rightarrow\infty} {\mathrm{lim}}{g}\left({b}\right)=\underset{{b}\rightarrow\infty} {\mathrm{lim}0}\:=\mathrm{0} \\ $$

Commented byJoel578 last updated on 20/Jan/19

thank you very much

$${thank}\:{you}\:{very}\:{much} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 19/Jan/19

b) it is my opinion... ∫_(−∞) ^(+∞) f(x)dx lim_(h→−∞) ∫_h ^0 f(x) dx=−ve A lim_(k→+∞) ∫_0 ^k f(x)dx=+ve A so ∫_(−∞) ^(+∞) ((2x)/(4+x^2 ))dx=0 anoother way... x=2tanθ dx=2sec^2 θdθ ∫_(−(π/2)) ^(π/2) ((2×2tanθ×2sec^2 θdθ)/(4+4tan^2 θ)) =∫_(−(π/2)) ^(π/2) ((8tanθsec^2 θ)/(4sec^2 θ))dθ =2∣lnsecθ∣_(−(π/2)) ^(π/2) =−2∣lncosθ∣_(−(π/2)) ^(π/2) =−2[lncos((π/2))−lncos(−(π/2))] =0 it is my opinion...let others comment...

$$\left.{b}\right)\:{it}\:{is}\:{my}\:{opinion}... \\ $$ $$\int_{−\infty} ^{+\infty} {f}\left({x}\right){dx} \\ $$ $$\underset{{h}\rightarrow−\infty} {\mathrm{lim}}\int_{{h}} ^{\mathrm{0}} \:{f}\left({x}\right)\:{dx}=−{ve}\:{A} \\ $$ $$\underset{{k}\rightarrow+\infty} {\mathrm{lim}}\:\int_{\mathrm{0}} ^{{k}} {f}\left({x}\right){dx}=+{ve}\:{A} \\ $$ $${so}\:\int_{−\infty} ^{+\infty} \frac{\mathrm{2}{x}}{\mathrm{4}+{x}^{\mathrm{2}} }{dx}=\mathrm{0} \\ $$ $${anoother}\:{way}... \\ $$ $${x}=\mathrm{2}{tan}\theta\:\:{dx}=\mathrm{2}{sec}^{\mathrm{2}} \theta{d}\theta \\ $$ $$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}×\mathrm{2}{tan}\theta×\mathrm{2}{sec}^{\mathrm{2}} \theta{d}\theta}{\mathrm{4}+\mathrm{4}{tan}^{\mathrm{2}} \theta} \\ $$ $$=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{8}{tan}\theta{sec}^{\mathrm{2}} \theta}{\mathrm{4}{sec}^{\mathrm{2}} \theta}{d}\theta \\ $$ $$=\mathrm{2}\mid{lnsec}\theta\mid_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \\ $$ $$=−\mathrm{2}\mid{lncos}\theta\mid_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \\ $$ $$=−\mathrm{2}\left[{lncos}\left(\frac{\pi}{\mathrm{2}}\right)−{lncos}\left(−\frac{\pi}{\mathrm{2}}\right)\right] \\ $$ $$=\mathrm{0} \\ $$ $${it}\:{is}\:{my}\:{opinion}...{let}\:{others}\:{comment}... \\ $$

Commented byJoel578 last updated on 20/Jan/19

thank you very much

$${thank}\:{you}\:{very}\:{much} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com