Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 50186 by rahul 19 last updated on 14/Dec/18

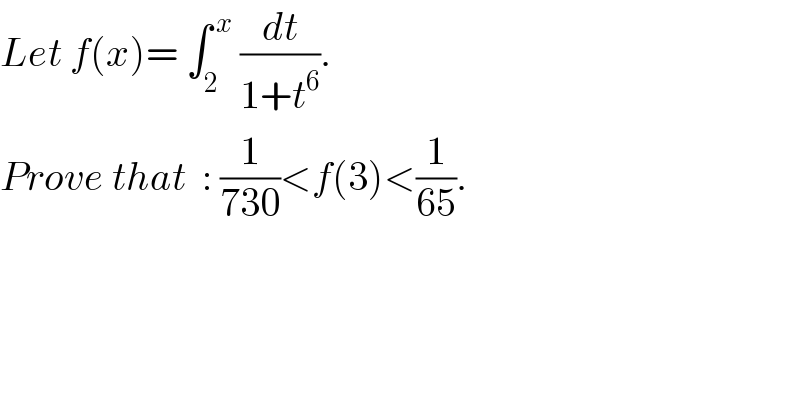
Let f(x)= ∫_2 ^( x) (dt/(1+t^6 )). Prove that : (1/(730))<f(3)<(1/(65)).

$${Let}\:{f}\left({x}\right)=\:\int_{\mathrm{2}} ^{\:{x}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{6}} }. \\ $$ $${Prove}\:{that}\:\::\:\frac{\mathrm{1}}{\mathrm{730}}<{f}\left(\mathrm{3}\right)<\frac{\mathrm{1}}{\mathrm{65}}. \\ $$

Answered by mr W last updated on 16/Dec/18

F(t)=(1/(1+t^6 )) is a decreasing function f(3)=∫_2 ^3 (dt/(1+t^6 )) f(3)<F(2)×(3−2)=F(2)=(1/(1+2^6 ))=(1/(1+64))=(1/(65)) f(3)>F(3)×(3−2)=F(3)=(1/(1+3^6 ))=(1/(1+9×9×9))=(1/(1+729))=(1/(730)) ⇒(1/(730))<f(3)<(1/(65))

$${F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{6}} }\:{is}\:{a}\:{decreasing}\:{function} \\ $$ $${f}\left(\mathrm{3}\right)=\int_{\mathrm{2}} ^{\mathrm{3}} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{6}} } \\ $$ $${f}\left(\mathrm{3}\right)<{F}\left(\mathrm{2}\right)×\left(\mathrm{3}−\mathrm{2}\right)={F}\left(\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\mathrm{6}} }=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{64}}=\frac{\mathrm{1}}{\mathrm{65}} \\ $$ $${f}\left(\mathrm{3}\right)>{F}\left(\mathrm{3}\right)×\left(\mathrm{3}−\mathrm{2}\right)={F}\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{3}^{\mathrm{6}} }=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{9}×\mathrm{9}×\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{729}}=\frac{\mathrm{1}}{\mathrm{730}} \\ $$ $$\Rightarrow\frac{\mathrm{1}}{\mathrm{730}}<{f}\left(\mathrm{3}\right)<\frac{\mathrm{1}}{\mathrm{65}} \\ $$

Commented bymr W last updated on 14/Dec/18

Commented bymr W last updated on 15/Dec/18

it is exact as you can see in the diagram. there exists such a point ξ. we know it exists, but we don′t know where it is. ∫_a ^b F(t)dt=area under the curve from a to b. if F(t) is decreasing, it′s obvious that ∫_a ^b F(t)dt<(b−a)F(a)=rectangle with max. height ∫_a ^b F(t)dt>(b−a)F(b)=rectangle with min. height if F(t) is increasing, it′s obvious that ∫_a ^b F(t)dt>(b−a)F(a) ∫_a ^b F(t)dt<(b−a)F(b)

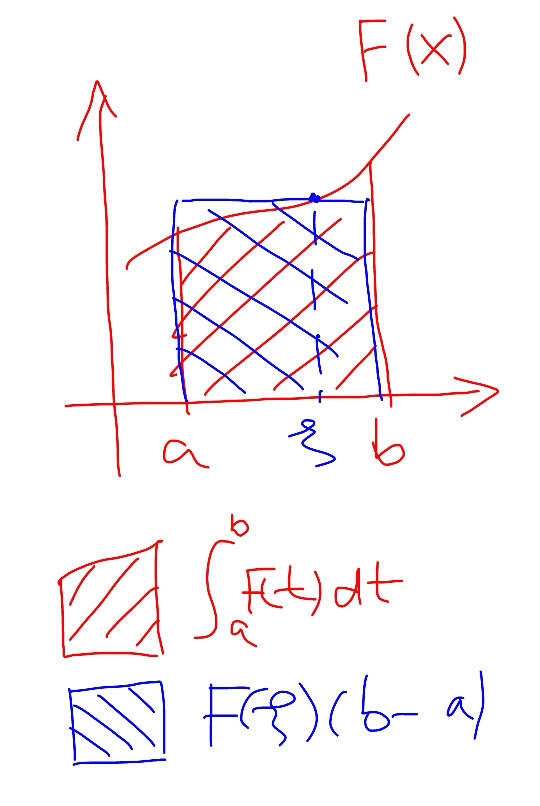
$${it}\:{is}\:{exact}\:{as}\:{you}\:{can}\:{see}\:{in}\:{the}\:{diagram}. \\ $$ $${there}\:{exists}\:{such}\:{a}\:{point}\:\xi.\:\:{we}\:{know} \\ $$ $${it}\:{exists},\:{but}\:{we}\:{don}'{t}\:{know}\:{where}\:{it} \\ $$ $${is}. \\ $$ $$\int_{{a}} ^{{b}} {F}\left({t}\right){dt}={area}\:{under}\:{the}\:{curve}\:{from}\:{a}\:{to}\:{b}. \\ $$ $$ \\ $$ $${if}\:{F}\left({t}\right)\:{is}\:{decreasing},\:{it}'{s}\:{obvious}\:{that} \\ $$ $$\int_{{a}} ^{{b}} {F}\left({t}\right){dt}<\left({b}−{a}\right){F}\left({a}\right)={rectangle}\:{with}\:{max}.\:{height} \\ $$ $$\int_{{a}} ^{{b}} {F}\left({t}\right){dt}>\left({b}−{a}\right){F}\left({b}\right)={rectangle}\:{with}\:{min}.\:{height} \\ $$ $$ \\ $$ $${if}\:{F}\left({t}\right)\:{is}\:{increasing},\:{it}'{s}\:{obvious}\:{that} \\ $$ $$\int_{{a}} ^{{b}} {F}\left({t}\right){dt}>\left({b}−{a}\right){F}\left({a}\right) \\ $$ $$\int_{{a}} ^{{b}} {F}\left({t}\right){dt}<\left({b}−{a}\right){F}\left({b}\right) \\ $$

Commented byrahul 19 last updated on 15/Dec/18

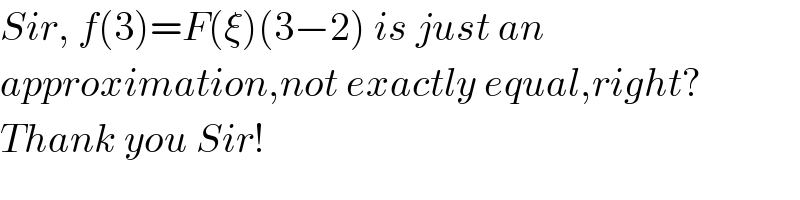
Sir, f(3)=F(ξ)(3−2) is just an approximation,not exactly equal,right? Thank you Sir!

$${Sir},\:{f}\left(\mathrm{3}\right)={F}\left(\xi\right)\left(\mathrm{3}−\mathrm{2}\right)\:{is}\:{just}\:{an}\: \\ $$ $${approximation},{not}\:{exactly}\:{equal},{right}? \\ $$ $${Thank}\:{you}\:{Sir}! \\ $$

Commented byrahul 19 last updated on 15/Dec/18

Perfect explaination!��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com