
Question Number 139323 by snipers237 last updated on 25/Apr/21
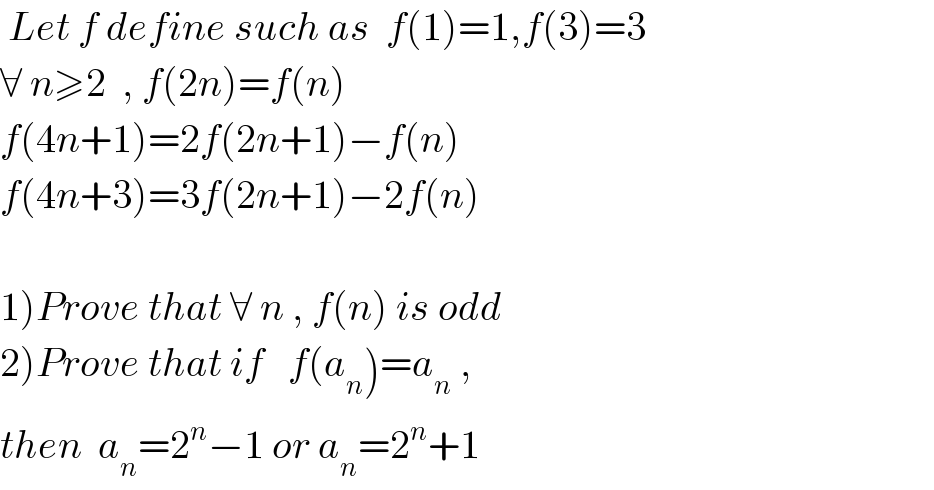
$$\:{Let}\:{f}\:{define}\:{such}\:{as}\:\:{f}\left(\mathrm{1}\right)=\mathrm{1},{f}\left(\mathrm{3}\right)=\mathrm{3} \\ $$$$\forall\:{n}\geqslant\mathrm{2}\:\:,\:{f}\left(\mathrm{2}{n}\right)={f}\left({n}\right)\: \\ $$$${f}\left(\mathrm{4}{n}+\mathrm{1}\right)=\mathrm{2}{f}\left(\mathrm{2}{n}+\mathrm{1}\right)−{f}\left({n}\right) \\ $$$${f}\left(\mathrm{4}{n}+\mathrm{3}\right)=\mathrm{3}{f}\left(\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{2}{f}\left({n}\right) \\ $$$$ \\ $$$$\left.\mathrm{1}\right){Prove}\:{that}\:\forall\:{n}\:,\:{f}\left({n}\right)\:{is}\:{odd} \\ $$$$\left.\mathrm{2}\right){Prove}\:{that}\:{if}\:\:\:{f}\left({a}_{{n}} \right)={a}_{{n}} \:, \\ $$$${then}\:\:{a}_{{n}} =\mathrm{2}^{{n}} −\mathrm{1}\:{or}\:{a}_{{n}} =\mathrm{2}^{{n}} +\mathrm{1} \\ $$
