Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 207085 by necx122 last updated on 06/May/24

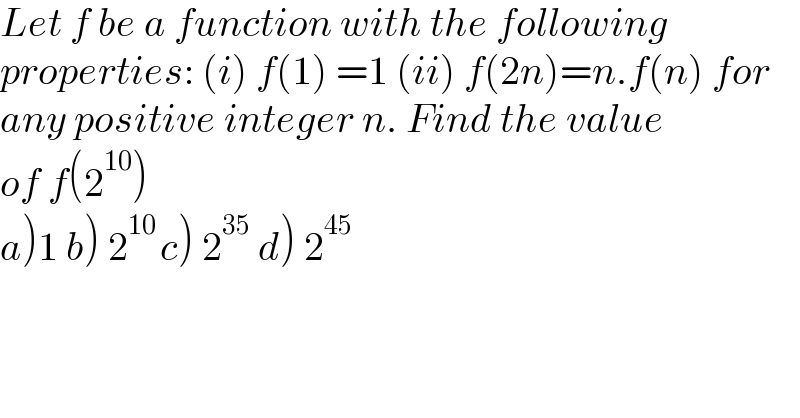
Let f be a function with the following properties: (i) f(1) =1 (ii) f(2n)=n.f(n) for any positive integer n. Find the value of f(2^(10) ) a)1 b) 2^(10 ) c) 2^(35) d) 2^(45)

$${Let}\:{f}\:{be}\:{a}\:{function}\:{with}\:{the}\:{following} \\ $$$${properties}:\:\left({i}\right)\:{f}\left(\mathrm{1}\right)\:=\mathrm{1}\:\left({ii}\right)\:{f}\left(\mathrm{2}{n}\right)={n}.{f}\left({n}\right)\:{for} \\ $$$${any}\:{positive}\:{integer}\:{n}.\:{Find}\:{the}\:{value} \\ $$$${of}\:{f}\left(\mathrm{2}^{\mathrm{10}} \right) \\ $$$$\left.{a}\left.\right)\left.\mathrm{1}\left.\:{b}\right)\:\mathrm{2}^{\mathrm{10}\:} {c}\right)\:\mathrm{2}^{\mathrm{35}} \:{d}\right)\:\mathrm{2}^{\mathrm{45}} \\ $$

Answered by A5T last updated on 06/May/24

f(2n)=nf(n) f(n)=(n/2)f((n/2))=(n/2)×(n/4)f((n/4)) =(n^q /2^(1+2+3+...+q) )f((n/2^q )) [by induction] ⇒f(2^(10) )=(((2^(10) )^(10) )/2^(1+2+3+...+10) )f((2^(10) /2^(10) ))=(2^(100) /2^(55) )=2^(45)

$${f}\left(\mathrm{2}{n}\right)={nf}\left({n}\right) \\ $$$${f}\left({n}\right)=\frac{{n}}{\mathrm{2}}{f}\left(\frac{{n}}{\mathrm{2}}\right)=\frac{{n}}{\mathrm{2}}×\frac{{n}}{\mathrm{4}}{f}\left(\frac{{n}}{\mathrm{4}}\right) \\ $$$$=\frac{{n}^{{q}} }{\mathrm{2}^{\mathrm{1}+\mathrm{2}+\mathrm{3}+...+{q}} }{f}\left(\frac{{n}}{\mathrm{2}^{{q}} }\right)\:\:\left[{by}\:{induction}\right] \\ $$$$\Rightarrow{f}\left(\mathrm{2}^{\mathrm{10}} \right)=\frac{\left(\mathrm{2}^{\mathrm{10}} \right)^{\mathrm{10}} }{\mathrm{2}^{\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{10}} }{f}\left(\frac{\mathrm{2}^{\mathrm{10}} }{\mathrm{2}^{\mathrm{10}} }\right)=\frac{\mathrm{2}^{\mathrm{100}} }{\mathrm{2}^{\mathrm{55}} }=\mathrm{2}^{\mathrm{45}} \\ $$

Commented by A5T last updated on 06/May/24

f(2^(10) )=f(2×2^9 )=2^9 ×f(2^9 )=2^9 ×[2^8 ×f(2^8 )] =2^(9+8) ×2^7 f(2^7 )=2^(9+8+7+...+3) ×2^2 f(2^2 ) =2^(9+8+7+...+2) ×2f(2)=2^(45)

$${f}\left(\mathrm{2}^{\mathrm{10}} \right)={f}\left(\mathrm{2}×\mathrm{2}^{\mathrm{9}} \right)=\mathrm{2}^{\mathrm{9}} ×{f}\left(\mathrm{2}^{\mathrm{9}} \right)=\mathrm{2}^{\mathrm{9}} ×\left[\mathrm{2}^{\mathrm{8}} ×{f}\left(\mathrm{2}^{\mathrm{8}} \right)\right] \\ $$$$=\mathrm{2}^{\mathrm{9}+\mathrm{8}} ×\mathrm{2}^{\mathrm{7}} {f}\left(\mathrm{2}^{\mathrm{7}} \right)=\mathrm{2}^{\mathrm{9}+\mathrm{8}+\mathrm{7}+...+\mathrm{3}} ×\mathrm{2}^{\mathrm{2}} {f}\left(\mathrm{2}^{\mathrm{2}} \right) \\ $$$$=\mathrm{2}^{\mathrm{9}+\mathrm{8}+\mathrm{7}+...+\mathrm{2}} ×\mathrm{2}{f}\left(\mathrm{2}\right)=\mathrm{2}^{\mathrm{45}} \\ $$

Commented by necx122 last updated on 06/May/24

Thank you sir. I know you tried your best to expain yet, I still dont understand

$${Thank}\:{you}\:{sir}.\:{I}\:{know}\:{you}\:{tried}\:{your} \\ $$$${best}\:{to}\:{expain}\:{yet},\:{I}\:{still}\:{dont}\:{understand} \\ $$

Commented by necx122 last updated on 06/May/24

This now, is very clear. Thank you so much great teacher.

$${This}\:{now},\:{is}\:{very}\:{clear}.\:{Thank}\:{you}\:{so} \\ $$$${much}\:{great}\:{teacher}. \\ $$

Answered by A5T last updated on 06/May/24

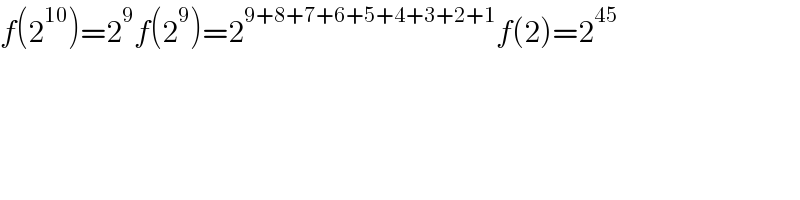
f(2^(10) )=2^9 f(2^9 )=2^(9+8+7+6+5+4+3+2+1) f(2)=2^(45)

$${f}\left(\mathrm{2}^{\mathrm{10}} \right)=\mathrm{2}^{\mathrm{9}} {f}\left(\mathrm{2}^{\mathrm{9}} \right)=\mathrm{2}^{\mathrm{9}+\mathrm{8}+\mathrm{7}+\mathrm{6}+\mathrm{5}+\mathrm{4}+\mathrm{3}+\mathrm{2}+\mathrm{1}} {f}\left(\mathrm{2}\right)=\mathrm{2}^{\mathrm{45}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com