Question and Answers Forum

All Questions      Topic List

Set Theory Questions

Previous in All Question      Next in All Question      

Previous in Set Theory      Next in Set Theory      

Question Number 216532 by sniper237 last updated on 11/Feb/25

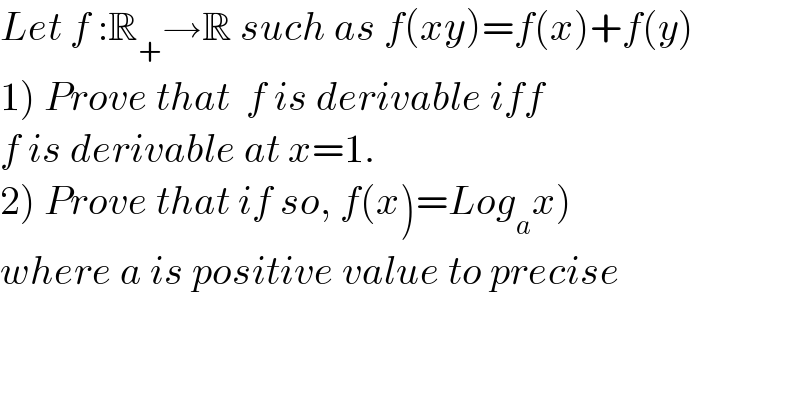
Let f :R_+ →R such as f(xy)=f(x)+f(y) 1) Prove that f is derivable iff f is derivable at x=1. 2) Prove that if so, f(x)=Log_a x) where a is positive value to precise

$${Let}\:{f}\::\mathbb{R}_{+} \rightarrow\mathbb{R}\:{such}\:{as}\:{f}\left({xy}\right)={f}\left({x}\right)+{f}\left({y}\right) \\ $$$$\left.\mathrm{1}\right)\:{Prove}\:{that}\:\:{f}\:{is}\:{derivable}\:{iff}\:\: \\ $$$${f}\:{is}\:{derivable}\:{at}\:{x}=\mathrm{1}. \\ $$$$\left.\mathrm{2}\left.\right)\:{Prove}\:{that}\:{if}\:{so},\:{f}\left({x}\right)={Log}_{{a}} {x}\right)\: \\ $$$${where}\:{a}\:{is}\:{positive}\:{value}\:{to}\:{precise} \\ $$

Answered by maths2 last updated on 11/Feb/25

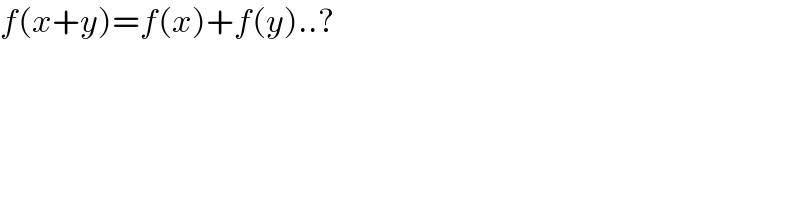
f(x+y)=f(x)+f(y)..?

$${f}\left({x}+{y}\right)={f}\left({x}\right)+{f}\left({y}\right)..? \\ $$$$ \\ $$

Commented by sniper237 last updated on 11/Feb/25

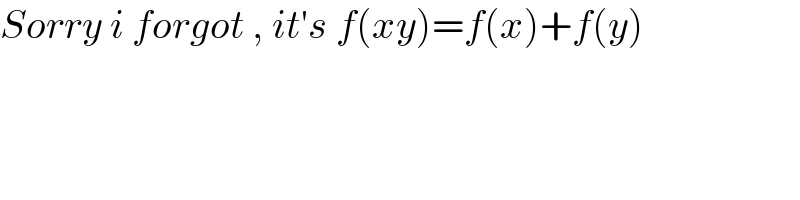
Sorry i forgot , it′s f(xy)=f(x)+f(y)

$${Sorry}\:{i}\:{forgot}\:,\:{it}'{s}\:{f}\left({xy}\right)={f}\left({x}\right)+{f}\left({y}\right) \\ $$

Answered by maths2 last updated on 13/Feb/25

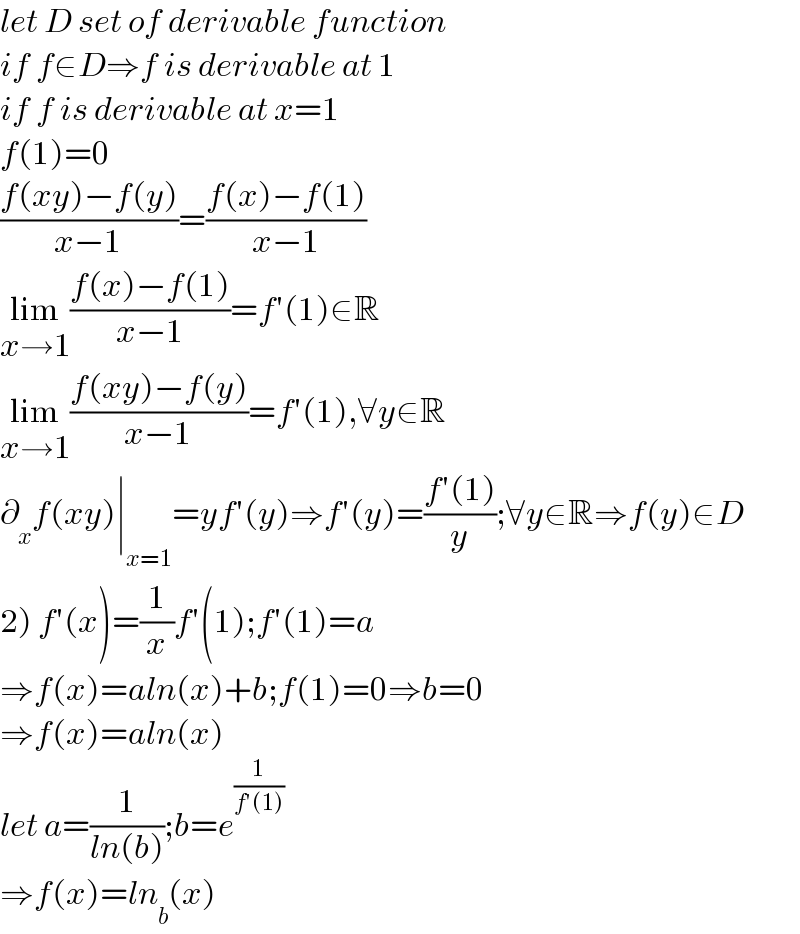
let D set of derivable function if f∈D⇒f is derivable at 1 if f is derivable at x=1 f(1)=0 ((f(xy)−f(y))/(x−1))=((f(x)−f(1))/(x−1)) lim_(x→1) ((f(x)−f(1))/(x−1))=f′(1)∈R lim_(x→1) ((f(xy)−f(y))/(x−1))=f′(1),∀y∈R ∂_x f(xy)∣_(x=1) =yf′(y)⇒f′(y)=((f′(1))/y);∀y∈R⇒f(y)∈D 2) f′(x)=(1/x)f′(1);f′(1)=a ⇒f(x)=aln(x)+b;f(1)=0⇒b=0 ⇒f(x)=aln(x) let a=(1/(ln(b)));b=e^(1/(f′(1))) ⇒f(x)=ln_b (x)

$${let}\:{D}\:{set}\:{of}\:{derivable}\:{function} \\ $$$${if}\:{f}\in{D}\Rightarrow{f}\:{is}\:{derivable}\:{at}\:\mathrm{1} \\ $$$${if}\:{f}\:{is}\:{derivable}\:{at}\:{x}=\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\frac{{f}\left({xy}\right)−{f}\left({y}\right)}{{x}−\mathrm{1}}=\frac{{f}\left({x}\right)−{f}\left(\mathrm{1}\right)}{{x}−\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{f}\left({x}\right)−{f}\left(\mathrm{1}\right)}{{x}−\mathrm{1}}={f}'\left(\mathrm{1}\right)\in\mathbb{R} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{f}\left({xy}\right)−{f}\left({y}\right)}{{x}−\mathrm{1}}={f}'\left(\mathrm{1}\right),\forall{y}\in\mathbb{R} \\ $$$$\partial_{{x}} {f}\left({xy}\right)\mid_{{x}=\mathrm{1}} ={yf}'\left({y}\right)\Rightarrow{f}'\left({y}\right)=\frac{{f}'\left(\mathrm{1}\right)}{{y}};\forall{y}\in\mathbb{R}\Rightarrow{f}\left({y}\right)\in{D} \\ $$$$\left.\mathrm{2}\right)\:{f}'\left({x}\right)=\frac{\mathrm{1}}{{x}}{f}'\left(\mathrm{1}\right);{f}'\left(\mathrm{1}\right)={a} \\ $$$$\Rightarrow{f}\left({x}\right)={aln}\left({x}\right)+{b};{f}\left(\mathrm{1}\right)=\mathrm{0}\Rightarrow{b}=\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)={aln}\left({x}\right) \\ $$$${let}\:{a}=\frac{\mathrm{1}}{{ln}\left({b}\right)};{b}={e}^{\frac{\mathrm{1}}{{f}'\left(\mathrm{1}\right)}} \\ $$$$\Rightarrow{f}\left({x}\right)={ln}_{{b}} \left({x}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com