
Previous in Relation and Functions Next in Relation and Functions
Question Number 13601 by Tinkutara last updated on 21/May/17
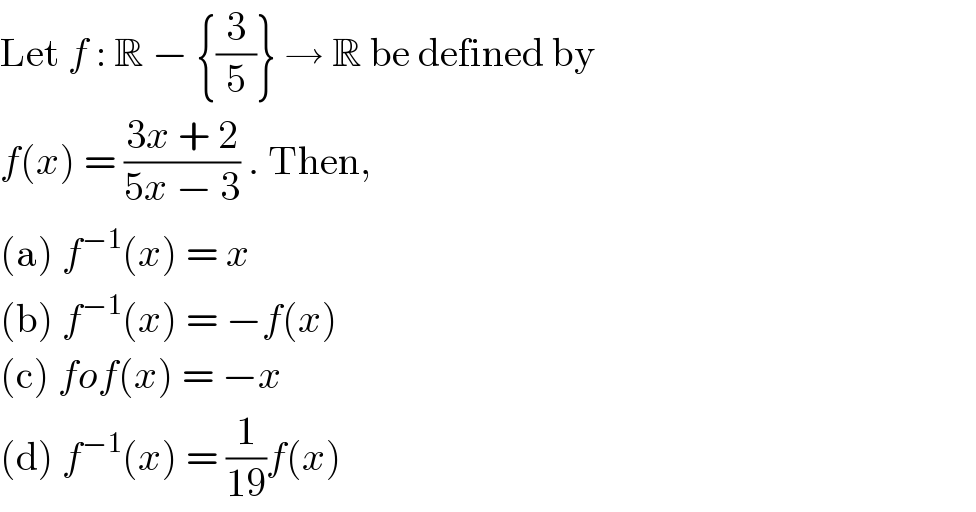
$$\mathrm{Let}\:{f}\::\:\mathbb{R}\:−\:\left\{\frac{\mathrm{3}}{\mathrm{5}}\right\}\:\rightarrow\:\mathbb{R}\:\mathrm{be}\:\mathrm{defined}\:\mathrm{by} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{3}{x}\:+\:\mathrm{2}}{\mathrm{5}{x}\:−\:\mathrm{3}}\:.\:\mathrm{Then}, \\ $$$$\left(\mathrm{a}\right)\:{f}^{−\mathrm{1}} \left({x}\right)\:=\:{x} \\ $$$$\left(\mathrm{b}\right)\:{f}^{−\mathrm{1}} \left({x}\right)\:=\:−{f}\left({x}\right) \\ $$$$\left(\mathrm{c}\right)\:{fof}\left({x}\right)\:=\:−{x} \\ $$$$\left(\mathrm{d}\right)\:{f}^{−\mathrm{1}} \left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{19}}{f}\left({x}\right) \\ $$
Answered by mrW1 last updated on 21/May/17

$${y}\:=\:\frac{\mathrm{3}{x}\:+\:\mathrm{2}}{\mathrm{5}{x}\:−\:\mathrm{3}} \\ $$$$\mathrm{5}{yx}−\mathrm{3}{y}=\mathrm{3}{x}+\mathrm{2} \\ $$$$\left(\mathrm{5}{y}−\mathrm{3}\right){x}=\mathrm{3}{y}+\mathrm{2} \\ $$$${x}=\frac{\mathrm{3}{y}+\mathrm{2}}{\mathrm{5}{y}−\mathrm{3}} \\ $$$$\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\frac{\mathrm{3}{x}+\mathrm{2}}{\mathrm{5}{x}−\mathrm{3}}={f}\left({x}\right) \\ $$$${fof}\left({x}\right)=\frac{\mathrm{3}\left(\frac{\mathrm{3}{x}+\mathrm{2}}{\mathrm{5}{x}−\mathrm{3}}\right)+\mathrm{2}}{\mathrm{5}\left(\frac{\mathrm{3}{x}+\mathrm{2}}{\mathrm{5}{x}−\mathrm{3}}\right)−\mathrm{3}}=\frac{\mathrm{9}{x}+\mathrm{6}+\mathrm{10}{x}−\mathrm{6}}{\mathrm{15}{x}+\mathrm{10}−\mathrm{15}{x}+\mathrm{9}}=\frac{\mathrm{19}{x}}{\mathrm{19}}={x} \\ $$$$ \\ $$$${no}\:{answer}\:{seems}\:{to}\:{be}\:{true}... \\ $$
