
Question Number 196872 by York12 last updated on 02/Sep/23
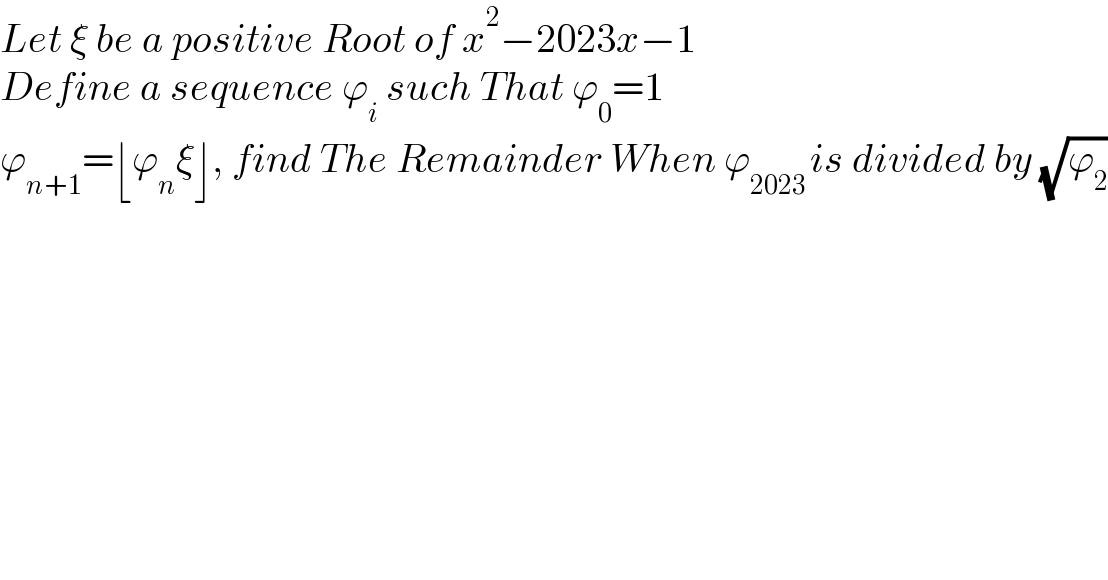
$${Let}\:\xi\:{be}\:{a}\:{positive}\:{Root}\:{of}\:{x}^{\mathrm{2}} −\mathrm{2023}{x}−\mathrm{1} \\ $$$${Define}\:{a}\:{sequence}\:\varphi_{{i}} \:{such}\:{That}\:\varphi_{\mathrm{0}} =\mathrm{1} \\ $$$$\varphi_{{n}+\mathrm{1}} =\lfloor\varphi_{{n}} \xi\rfloor,\:{find}\:{The}\:{Remainder}\:{When}\:\varphi_{\mathrm{2023}\:} {is}\:{divided}\:{by}\:\sqrt{\varphi_{\mathrm{2}} } \\ $$
Answered by York12 last updated on 02/Sep/23
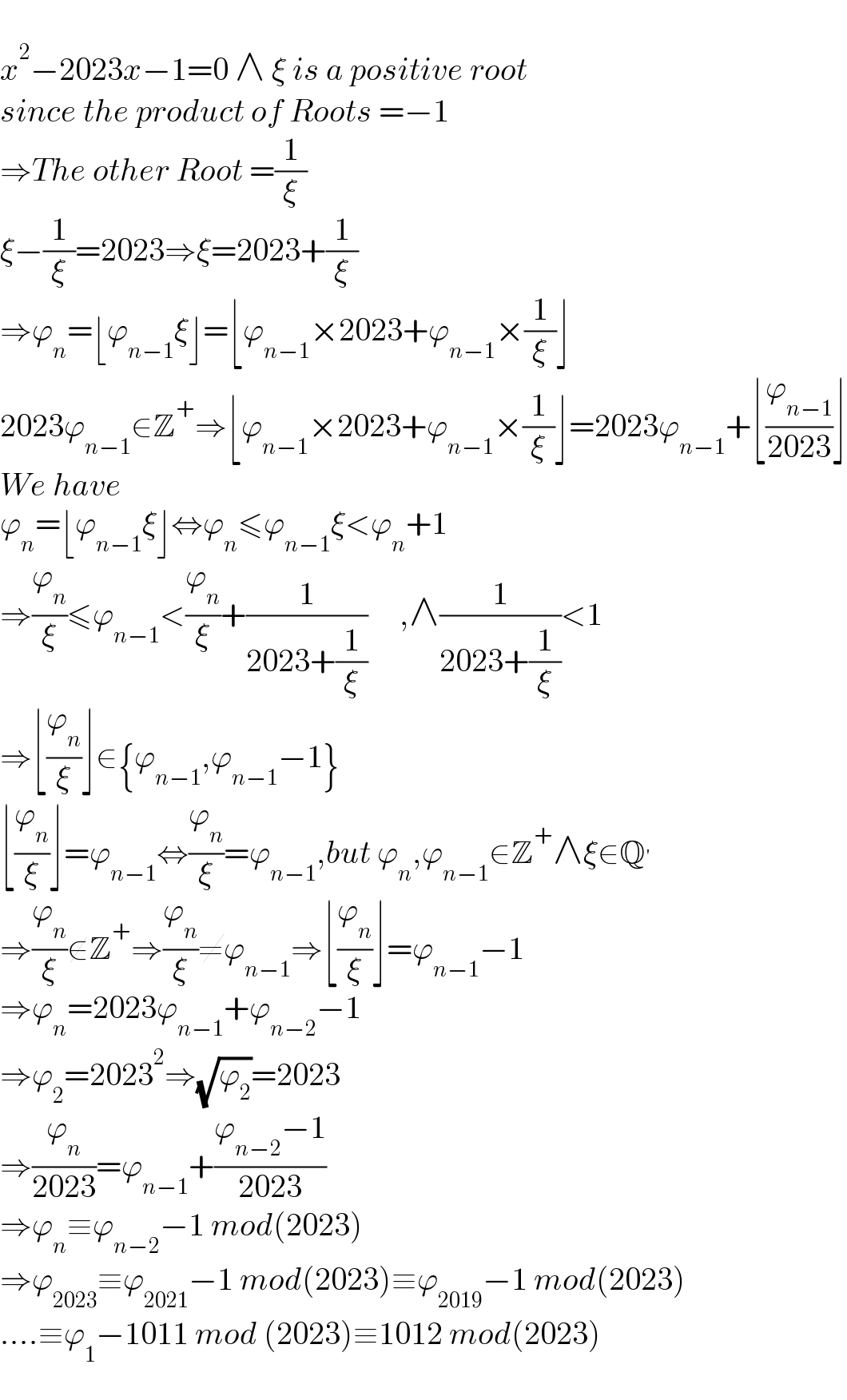
$$ \\ $$$${x}^{\mathrm{2}} −\mathrm{2023}{x}−\mathrm{1}=\mathrm{0}\:\wedge\:\xi\:{is}\:{a}\:{positive}\:{root}\: \\ $$$${since}\:{the}\:{product}\:{of}\:{Roots}\:=−\mathrm{1} \\ $$$$\Rightarrow{The}\:{other}\:{Root}\:=\frac{\mathrm{1}}{\xi} \\ $$$$\xi−\frac{\mathrm{1}}{\xi}=\mathrm{2023}\Rightarrow\xi=\mathrm{2023}+\frac{\mathrm{1}}{\xi} \\ $$$$\Rightarrow\varphi_{{n}} =\lfloor\varphi_{{n}−\mathrm{1}} \xi\rfloor=\lfloor\varphi_{{n}−\mathrm{1}} ×\mathrm{2023}+\varphi_{{n}−\mathrm{1}} ×\frac{\mathrm{1}}{\xi}\rfloor \\ $$$$\mathrm{2023}\varphi_{{n}−\mathrm{1}} \in\mathbb{Z}^{+} \Rightarrow\lfloor\varphi_{{n}−\mathrm{1}} ×\mathrm{2023}+\varphi_{{n}−\mathrm{1}} ×\frac{\mathrm{1}}{\xi}\rfloor=\mathrm{2023}\varphi_{{n}−\mathrm{1}} +\lfloor\frac{\varphi_{{n}−\mathrm{1}} }{\mathrm{2023}}\rfloor \\ $$$${We}\:{have} \\ $$$$\varphi_{{n}} =\lfloor\varphi_{{n}−\mathrm{1}} \xi\rfloor\Leftrightarrow\varphi_{{n}} \leqslant\varphi_{{n}−\mathrm{1}} \xi<\varphi_{{n}} +\mathrm{1} \\ $$$$\Rightarrow\frac{\varphi_{{n}} }{\xi}\leqslant\varphi_{{n}−\mathrm{1}} <\frac{\varphi_{{n}} }{\xi}+\frac{\mathrm{1}}{\mathrm{2023}+\frac{\mathrm{1}}{\xi}}\:\:\:\:\:,\wedge\frac{\mathrm{1}}{\mathrm{2023}+\frac{\mathrm{1}}{\xi}}<\mathrm{1} \\ $$$$\Rightarrow\lfloor\frac{\varphi_{{n}} }{\xi}\rfloor\in\left\{\varphi_{{n}−\mathrm{1}} ,\varphi_{{n}−\mathrm{1}} −\mathrm{1}\right\} \\ $$$$\lfloor\frac{\varphi_{{n}} }{\xi}\rfloor=\varphi_{{n}−\mathrm{1}} \Leftrightarrow\frac{\varphi_{{n}} }{\xi}=\varphi_{{n}−\mathrm{1}} ,{but}\:\varphi_{{n}} ,\varphi_{{n}−\mathrm{1}} \in\mathbb{Z}^{+} \wedge\xi\in\mathbb{Q}^{'} \\ $$$$\Rightarrow\frac{\varphi_{{n}} }{\xi}\notin\mathbb{Z}^{+} \Rightarrow\frac{\varphi_{{n}} }{\xi}\neq\varphi_{{n}−\mathrm{1}} \Rightarrow\lfloor\frac{\varphi_{{n}} }{\xi}\rfloor=\varphi_{{n}−\mathrm{1}} −\mathrm{1} \\ $$$$\Rightarrow\varphi_{{n}} =\mathrm{2023}\varphi_{{n}−\mathrm{1}} +\varphi_{{n}−\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\varphi_{\mathrm{2}} =\mathrm{2023}^{\mathrm{2}} \Rightarrow\sqrt{\varphi_{\mathrm{2}} }=\mathrm{2023} \\ $$$$\Rightarrow\frac{\varphi_{{n}} }{\mathrm{2023}}=\varphi_{{n}−\mathrm{1}} +\frac{\varphi_{{n}−\mathrm{2}} −\mathrm{1}}{\mathrm{2023}} \\ $$$$\Rightarrow\varphi_{{n}} \equiv\varphi_{{n}−\mathrm{2}} −\mathrm{1}\:{mod}\left(\mathrm{2023}\right) \\ $$$$\Rightarrow\varphi_{\mathrm{2023}} \equiv\varphi_{\mathrm{2021}} −\mathrm{1}\:{mod}\left(\mathrm{2023}\right)\equiv\varphi_{\mathrm{2019}} −\mathrm{1}\:{mod}\left(\mathrm{2023}\right) \\ $$$$....\equiv\varphi_{\mathrm{1}} −\mathrm{1011}\:{mod}\:\left(\mathrm{2023}\right)\equiv\mathrm{1012}\:{mod}\left(\mathrm{2023}\right) \\ $$
