Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 200836 by Rasheed.Sindhi last updated on 24/Nov/23

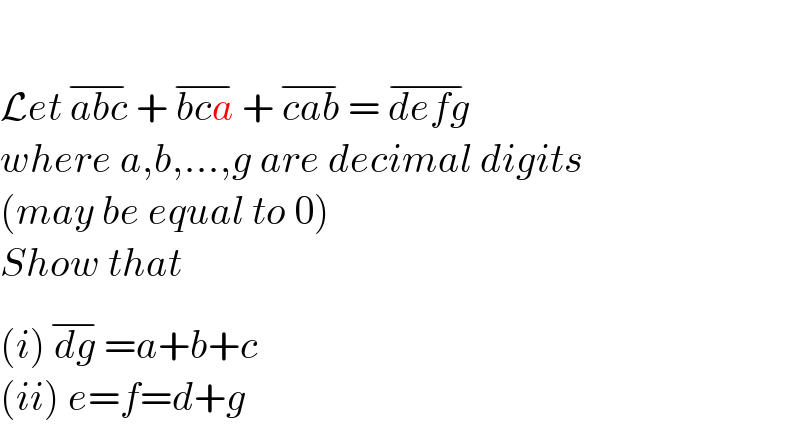
Let abc ^(−) + bca ^(−) + cab ^(−) = defg ^(−) where a,b,...,g are decimal digits (may be equal to 0) Show that (i) dg ^(−) =a+b+c (ii) e=f=d+g

$$ \\ $$$$\mathcal{L}{et}\overline {\:{abc}\:}+\overline {\:{bca}\:}+\overline {\:{cab}\:}=\overline {\:{defg}\:} \\ $$$${where}\:{a},{b},...,{g}\:{are}\:{decimal}\:{digits} \\ $$$$\left({may}\:{be}\:{equal}\:{to}\:\mathrm{0}\right)\: \\ $$$${Show}\:{that} \\ $$$$\left({i}\right)\overline {\:{dg}\:}={a}+{b}+{c} \\ $$$$\left({ii}\right)\:{e}={f}={d}+{g} \\ $$

Commented by LaChicaFrancesa last updated on 24/Nov/23

Hola, soy nueva en la app y quería consultar cómo se hace para que las 3 letras lleven encima la barra. Qué símbolo se usa?

Commented by deleteduser1 last updated on 24/Nov/23

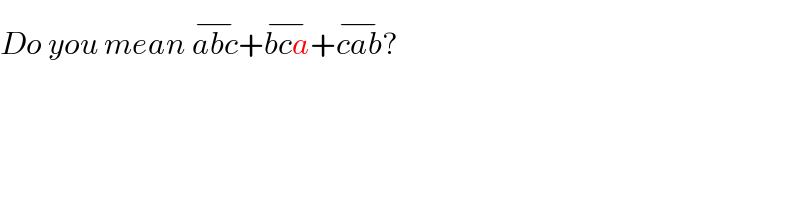
Do you mean abc^(−) +bca^(−) +cab^(−) ?

$${Do}\:{you}\:{mean}\:\overline {{abc}}+\overline {{bca}}+\overline {{cab}}? \\ $$

Commented by Rasheed.Sindhi last updated on 24/Nov/23

Yes sir, exactly!

$${Yes}\:{sir},\:{exactly}! \\ $$

Commented by deleteduser1 last updated on 24/Nov/23

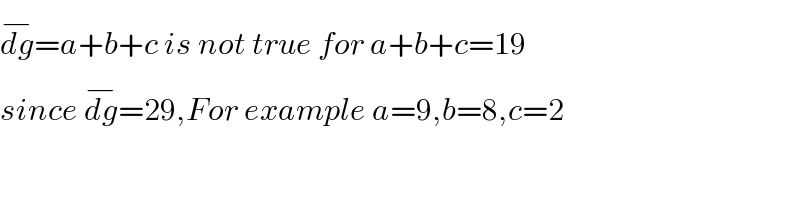
dg^(−) =a+b+c is not true for a+b+c=19 since dg^(−) =29,For example a=9,b=8,c=2

$$\overline {{dg}}={a}+{b}+{c}\:{is}\:{not}\:{true}\:{for}\:{a}+{b}+{c}=\mathrm{19} \\ $$$${since}\:\overline {{dg}}=\mathrm{29},{For}\:{example}\:{a}=\mathrm{9},{b}=\mathrm{8},{c}=\mathrm{2} \\ $$

Answered by deleteduser1 last updated on 24/Nov/23

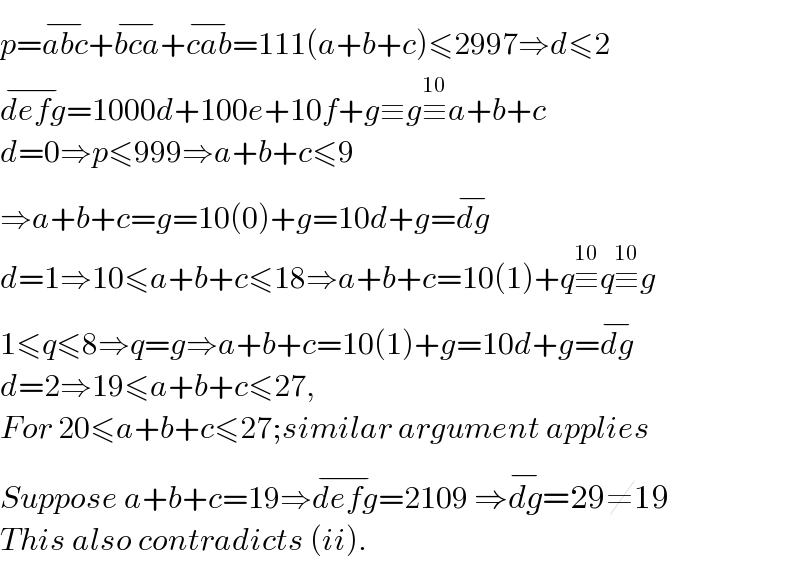
p=abc^(−) +bca^(−) +cab^(−) =111(a+b+c)≤2997⇒d≤2 defg^(−) =1000d+100e+10f+g≡g≡^(10) a+b+c d=0⇒p≤999⇒a+b+c≤9 ⇒a+b+c=g=10(0)+g=10d+g=dg^(−) d=1⇒10≤a+b+c≤18⇒a+b+c=10(1)+q≡^(10) q≡^(10) g 1≤q≤8⇒q=g⇒a+b+c=10(1)+g=10d+g=dg^(−) d=2⇒19≤a+b+c≤27, For 20≤a+b+c≤27;similar argument applies Suppose a+b+c=19⇒defg^(−) =2109 ⇒dg^(−) =29≠19 This also contradicts (ii).

$${p}=\overline {{abc}}+\overline {{bca}}+\overline {{cab}}=\mathrm{111}\left({a}+{b}+{c}\right)\leqslant\mathrm{2997}\Rightarrow{d}\leqslant\mathrm{2} \\ $$$$\overline {{defg}}=\mathrm{1000}{d}+\mathrm{100}{e}+\mathrm{10}{f}+{g}\equiv{g}\overset{\mathrm{10}} {\equiv}{a}+{b}+{c} \\ $$$${d}=\mathrm{0}\Rightarrow{p}\leqslant\mathrm{999}\Rightarrow{a}+{b}+{c}\leqslant\mathrm{9} \\ $$$$\Rightarrow{a}+{b}+{c}={g}=\mathrm{10}\left(\mathrm{0}\right)+{g}=\mathrm{10}{d}+{g}=\overline {{dg}} \\ $$$${d}=\mathrm{1}\Rightarrow\mathrm{10}\leqslant{a}+{b}+{c}\leqslant\mathrm{18}\Rightarrow{a}+{b}+{c}=\mathrm{10}\left(\mathrm{1}\right)+{q}\overset{\mathrm{10}} {\equiv}{q}\overset{\mathrm{10}} {\equiv}{g} \\ $$$$\mathrm{1}\leqslant{q}\leqslant\mathrm{8}\Rightarrow{q}={g}\Rightarrow{a}+{b}+{c}=\mathrm{10}\left(\mathrm{1}\right)+{g}=\mathrm{10}{d}+{g}=\overline {{dg}} \\ $$$${d}=\mathrm{2}\Rightarrow\mathrm{19}\leqslant{a}+{b}+{c}\leqslant\mathrm{27},\: \\ $$$${For}\:\mathrm{20}\leqslant{a}+{b}+{c}\leqslant\mathrm{27};{similar}\:{argument}\:{applies} \\ $$$${Suppose}\:{a}+{b}+{c}=\mathrm{19}\Rightarrow\overline {{defg}}=\mathrm{2109}\:\Rightarrow\overline {{dg}}=\mathrm{29}\neq\mathrm{19} \\ $$$${This}\:{also}\:{contradicts}\:\left({ii}\right). \\ $$

Commented by Rasheed.Sindhi last updated on 24/Nov/23

V. nice analysis! Thanks sir! The statement is not true in a few cases, of course.However your counter example may be justified if we be allowed decimal digits greater than 9 also. Let X is digit having value10 982+829+298=1XX9 =1000+100(10)+10(10)+9=2109 Anyway you′re very right because decimal digit may not exceed than 9.

$$\mathrm{V}.\:\mathrm{nice}\:\mathrm{analysis}! \\ $$$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\boldsymbol{\mathrm{sir}}! \\ $$$$\mathcal{T}{he}\:{statement}\:{is}\:{not}\:{true}\:{in}\:{a}\: \\ $$$${few}\:{cases},\:{of}\:{course}.{However} \\ $$$${your}\:{counter}\:{example}\:{may}\:{be}\: \\ $$$${justified}\:{if}\:{we}\:{be}\:{allowed}\:{decimal} \\ $$$${digits}\:{greater}\:{than}\:\mathrm{9}\:{also}. \\ $$$${Let}\:\mathrm{X}\:{is}\:{digit}\:{having}\:{value}\mathrm{10} \\ $$$$\mathrm{982}+\mathrm{829}+\mathrm{298}=\mathrm{1XX9} \\ $$$$\:\:\:=\mathrm{1000}+\mathrm{100}\left(\mathrm{10}\right)+\mathrm{10}\left(\mathrm{10}\right)+\mathrm{9}=\mathrm{2109} \\ $$$${Anyway}\:\boldsymbol{{you}}'\boldsymbol{{re}}\:\boldsymbol{{very}}\:\boldsymbol{{right}}\:{because} \\ $$$${decimal}\:{digit}\:{may}\:{not}\:{exceed} \\ $$$$\:{than}\:\mathrm{9}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com