Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 216646 by York12 last updated on 13/Feb/25

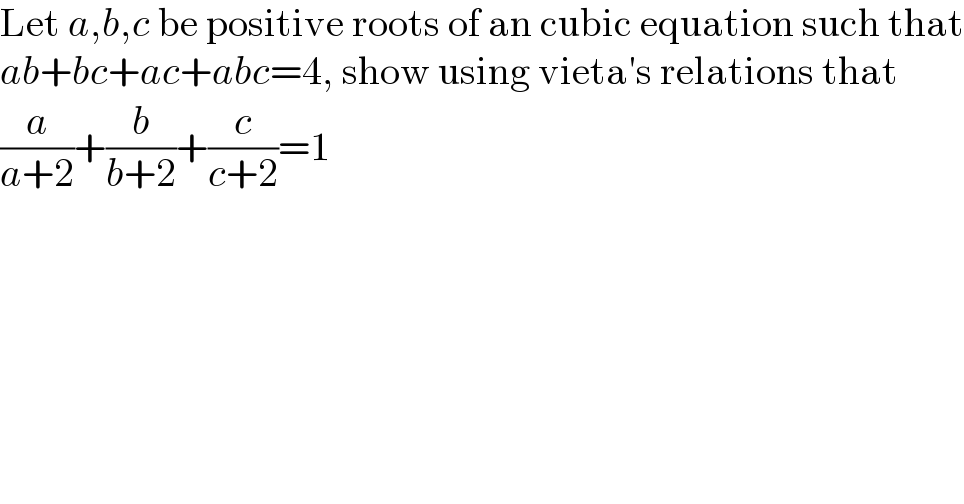
Let a,b,c be positive roots of an cubic equation such that ab+bc+ac+abc=4, show using vieta′s relations that (a/(a+2))+(b/(b+2))+(c/(c+2))=1

$$\mathrm{Let}\:{a},{b},{c}\:\mathrm{be}\:\mathrm{positive}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{an}\:\mathrm{cubic}\:\mathrm{equation}\:\mathrm{such}\:\mathrm{that} \\ $$$${ab}+{bc}+{ac}+{abc}=\mathrm{4},\:\mathrm{show}\:\mathrm{using}\:\mathrm{vieta}'\mathrm{s}\:\mathrm{relations}\:\mathrm{that} \\ $$$$\frac{{a}}{{a}+\mathrm{2}}+\frac{{b}}{{b}+\mathrm{2}}+\frac{{c}}{{c}+\mathrm{2}}=\mathrm{1} \\ $$

Answered by A5T last updated on 14/Feb/25

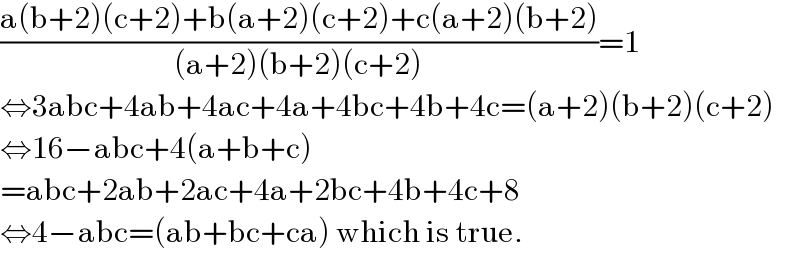
((a(b+2)(c+2)+b(a+2)(c+2)+c(a+2)(b+2))/((a+2)(b+2)(c+2)))=1 ⇔3abc+4ab+4ac+4a+4bc+4b+4c=(a+2)(b+2)(c+2) ⇔16−abc+4(a+b+c) =abc+2ab+2ac+4a+2bc+4b+4c+8 ⇔4−abc=(ab+bc+ca) which is true.

$$\frac{\mathrm{a}\left(\mathrm{b}+\mathrm{2}\right)\left(\mathrm{c}+\mathrm{2}\right)+\mathrm{b}\left(\mathrm{a}+\mathrm{2}\right)\left(\mathrm{c}+\mathrm{2}\right)+\mathrm{c}\left(\mathrm{a}+\mathrm{2}\right)\left(\mathrm{b}+\mathrm{2}\right)}{\left(\mathrm{a}+\mathrm{2}\right)\left(\mathrm{b}+\mathrm{2}\right)\left(\mathrm{c}+\mathrm{2}\right)}=\mathrm{1} \\ $$$$\Leftrightarrow\mathrm{3abc}+\mathrm{4ab}+\mathrm{4ac}+\mathrm{4a}+\mathrm{4bc}+\mathrm{4b}+\mathrm{4c}=\left(\mathrm{a}+\mathrm{2}\right)\left(\mathrm{b}+\mathrm{2}\right)\left(\mathrm{c}+\mathrm{2}\right) \\ $$$$\Leftrightarrow\mathrm{16}−\mathrm{abc}+\mathrm{4}\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right) \\ $$$$=\mathrm{abc}+\mathrm{2ab}+\mathrm{2ac}+\mathrm{4a}+\mathrm{2bc}+\mathrm{4b}+\mathrm{4c}+\mathrm{8} \\ $$$$\Leftrightarrow\mathrm{4}−\mathrm{abc}=\left(\mathrm{ab}+\mathrm{bc}+\mathrm{ca}\right)\:\mathrm{which}\:\mathrm{is}\:\mathrm{true}. \\ $$

Commented by York12 last updated on 14/Feb/25

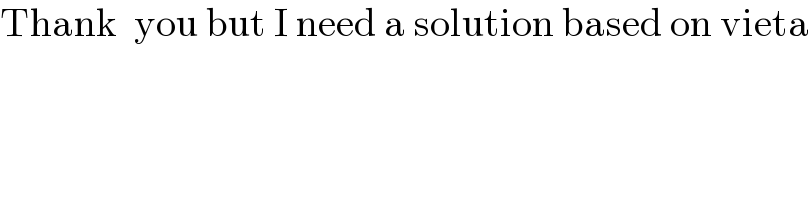
Thank you but I need a solution based on vieta

$$\mathrm{Thank}\:\:\mathrm{you}\:\mathrm{but}\:\mathrm{I}\:\mathrm{need}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{based}\:\mathrm{on}\:\mathrm{vieta} \\ $$

Answered by Rasheed.Sindhi last updated on 14/Feb/25

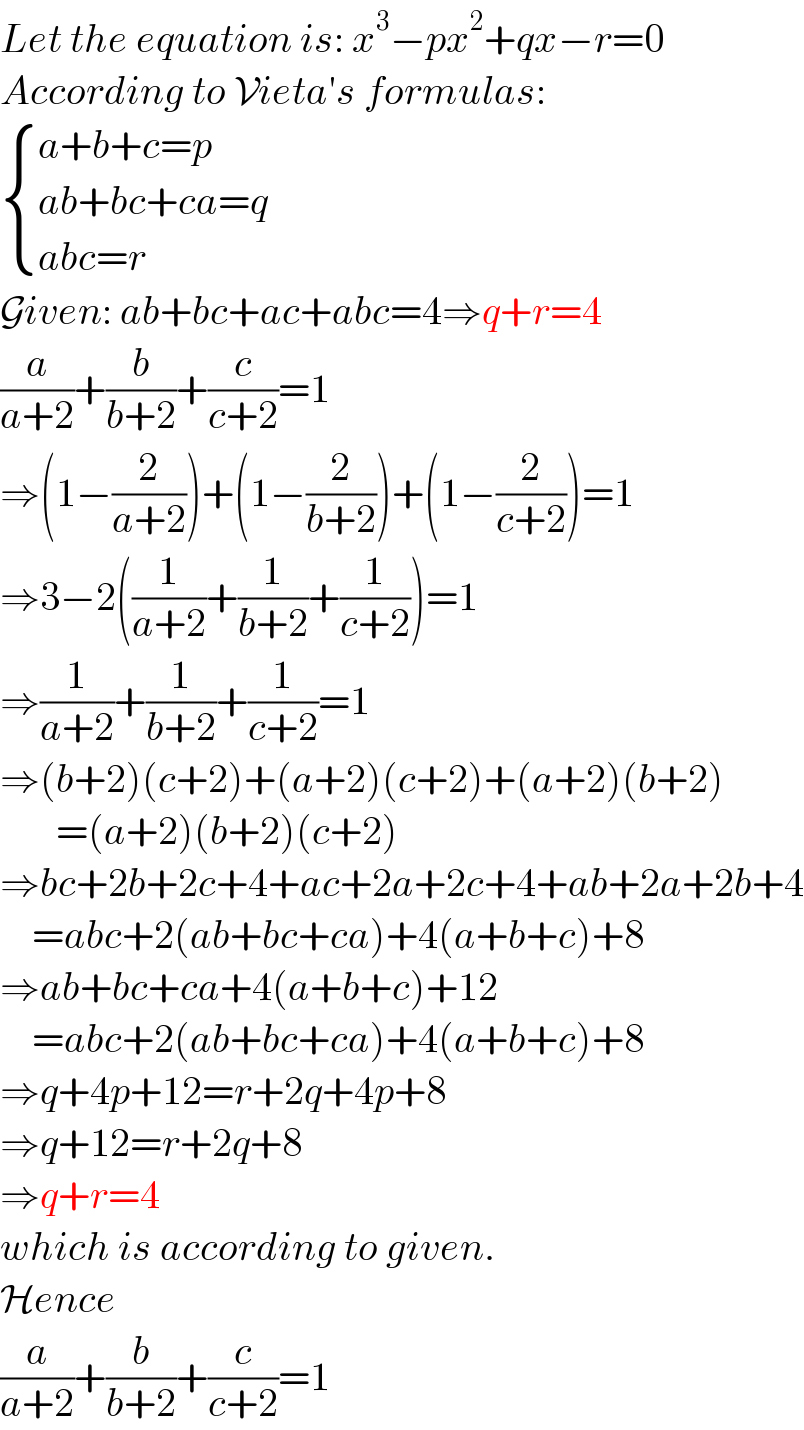
Let the equation is: x^3 −px^2 +qx−r=0 According to Vieta′s formulas: { ((a+b+c=p)),((ab+bc+ca=q)),((abc=r)) :} Given: ab+bc+ac+abc=4⇒q+r=4 (a/(a+2))+(b/(b+2))+(c/(c+2))=1 ⇒(1−(2/(a+2)))+(1−(2/(b+2)))+(1−(2/(c+2)))=1 ⇒3−2((1/(a+2))+(1/(b+2))+(1/(c+2)))=1 ⇒(1/(a+2))+(1/(b+2))+(1/(c+2))=1 ⇒(b+2)(c+2)+(a+2)(c+2)+(a+2)(b+2) =(a+2)(b+2)(c+2) ⇒bc+2b+2c+4+ac+2a+2c+4+ab+2a+2b+4 =abc+2(ab+bc+ca)+4(a+b+c)+8 ⇒ab+bc+ca+4(a+b+c)+12 =abc+2(ab+bc+ca)+4(a+b+c)+8 ⇒q+4p+12=r+2q+4p+8 ⇒q+12=r+2q+8 ⇒q+r=4 which is according to given. Hence (a/(a+2))+(b/(b+2))+(c/(c+2))=1

$${Let}\:{the}\:{equation}\:{is}:\:{x}^{\mathrm{3}} −{px}^{\mathrm{2}} +{qx}−{r}=\mathrm{0} \\ $$$${According}\:{to}\:\mathcal{V}{ieta}'{s}\:{formulas}: \\ $$$$\begin{cases}{{a}+{b}+{c}={p}}\\{{ab}+{bc}+{ca}={q}}\\{{abc}={r}}\end{cases} \\ $$$$\mathcal{G}{iven}:\:{ab}+{bc}+{ac}+{abc}=\mathrm{4}\Rightarrow{q}+{r}=\mathrm{4} \\ $$$$\frac{{a}}{{a}+\mathrm{2}}+\frac{{b}}{{b}+\mathrm{2}}+\frac{{c}}{{c}+\mathrm{2}}=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{1}−\frac{\mathrm{2}}{{a}+\mathrm{2}}\right)+\left(\mathrm{1}−\frac{\mathrm{2}}{{b}+\mathrm{2}}\right)+\left(\mathrm{1}−\frac{\mathrm{2}}{{c}+\mathrm{2}}\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{3}−\mathrm{2}\left(\frac{\mathrm{1}}{{a}+\mathrm{2}}+\frac{\mathrm{1}}{{b}+\mathrm{2}}+\frac{\mathrm{1}}{{c}+\mathrm{2}}\right)=\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{a}+\mathrm{2}}+\frac{\mathrm{1}}{{b}+\mathrm{2}}+\frac{\mathrm{1}}{{c}+\mathrm{2}}=\mathrm{1} \\ $$$$\Rightarrow\left({b}+\mathrm{2}\right)\left({c}+\mathrm{2}\right)+\left({a}+\mathrm{2}\right)\left({c}+\mathrm{2}\right)+\left({a}+\mathrm{2}\right)\left({b}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:=\left({a}+\mathrm{2}\right)\left({b}+\mathrm{2}\right)\left({c}+\mathrm{2}\right) \\ $$$$\Rightarrow{bc}+\mathrm{2}{b}+\mathrm{2}{c}+\mathrm{4}+{ac}+\mathrm{2}{a}+\mathrm{2}{c}+\mathrm{4}+{ab}+\mathrm{2}{a}+\mathrm{2}{b}+\mathrm{4} \\ $$$$\:\:\:\:={abc}+\mathrm{2}\left({ab}+{bc}+{ca}\right)+\mathrm{4}\left({a}+{b}+{c}\right)+\mathrm{8} \\ $$$$\Rightarrow{ab}+{bc}+{ca}+\mathrm{4}\left({a}+{b}+{c}\right)+\mathrm{12} \\ $$$$\:\:\:\:={abc}+\mathrm{2}\left({ab}+{bc}+{ca}\right)+\mathrm{4}\left({a}+{b}+{c}\right)+\mathrm{8} \\ $$$$\Rightarrow{q}+\mathrm{4}{p}+\mathrm{12}={r}+\mathrm{2}{q}+\mathrm{4}{p}+\mathrm{8} \\ $$$$\Rightarrow{q}+\mathrm{12}={r}+\mathrm{2}{q}+\mathrm{8} \\ $$$$\Rightarrow{q}+{r}=\mathrm{4}\: \\ $$$${which}\:{is}\:{according}\:{to}\:{given}. \\ $$$$\mathcal{H}{ence}\: \\ $$$$\frac{{a}}{{a}+\mathrm{2}}+\frac{{b}}{{b}+\mathrm{2}}+\frac{{c}}{{c}+\mathrm{2}}=\mathrm{1} \\ $$

Answered by Rasheed.Sindhi last updated on 14/Feb/25

(a/(a+2))+(b/(b+2))+(c/(c+2))=1 (a/(a+2))−1+(b/(b+2))−1+(c/(c+2))−1=1−3 ((−2)/(a+2))+((−2)/(b+2))+((−2)/(c+2))=−2 (1/(a+2))+(1/(b+2))+(1/(c+2))=1 ▶(b+2)(c+2)+(a+2)(c+2)+(a+2)(b+2) =(a+2)(b+2)(c+2) ▶ab+bc+ca+12+4(a+b+c) =abc+2(ab+bc+ca)+4(a+b+c)+8 ▶ab+bc+ca+12 =abc+2(ab+bc+ca)+8 ▶ ab+bc+ca+abc=4 (Given) Hence (a/(a+2))+(b/(b+2))+(c/(c+2))=1

$$ \\ $$$$\frac{{a}}{{a}+\mathrm{2}}+\frac{{b}}{{b}+\mathrm{2}}+\frac{{c}}{{c}+\mathrm{2}}=\mathrm{1} \\ $$$$\frac{{a}}{{a}+\mathrm{2}}−\mathrm{1}+\frac{{b}}{{b}+\mathrm{2}}−\mathrm{1}+\frac{{c}}{{c}+\mathrm{2}}−\mathrm{1}=\mathrm{1}−\mathrm{3} \\ $$$$\frac{−\mathrm{2}}{{a}+\mathrm{2}}+\frac{−\mathrm{2}}{{b}+\mathrm{2}}+\frac{−\mathrm{2}}{{c}+\mathrm{2}}=−\mathrm{2} \\ $$$$\frac{\mathrm{1}}{{a}+\mathrm{2}}+\frac{\mathrm{1}}{{b}+\mathrm{2}}+\frac{\mathrm{1}}{{c}+\mathrm{2}}=\mathrm{1} \\ $$$$\blacktriangleright\left({b}+\mathrm{2}\right)\left({c}+\mathrm{2}\right)+\left({a}+\mathrm{2}\right)\left({c}+\mathrm{2}\right)+\left({a}+\mathrm{2}\right)\left({b}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:=\left({a}+\mathrm{2}\right)\left({b}+\mathrm{2}\right)\left({c}+\mathrm{2}\right) \\ $$$$\blacktriangleright{ab}+{bc}+{ca}+\mathrm{12}+\mathrm{4}\left({a}+{b}+{c}\right) \\ $$$$\:\:\:\:\:\:={abc}+\mathrm{2}\left({ab}+{bc}+{ca}\right)+\mathrm{4}\left({a}+{b}+{c}\right)+\mathrm{8} \\ $$$$\blacktriangleright{ab}+{bc}+{ca}+\mathrm{12} \\ $$$$\:\:\:\:\:\:={abc}+\mathrm{2}\left({ab}+{bc}+{ca}\right)+\mathrm{8} \\ $$$$\blacktriangleright\:{ab}+{bc}+{ca}+{abc}=\mathrm{4}\:\left({Given}\right) \\ $$$$\mathcal{H}{ence} \\ $$$$\:\:\:\:\:\frac{{a}}{{a}+\mathrm{2}}+\frac{{b}}{{b}+\mathrm{2}}+\frac{{c}}{{c}+\mathrm{2}}=\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com