
Question Number 42133 by rahul 19 last updated on 18/Aug/18
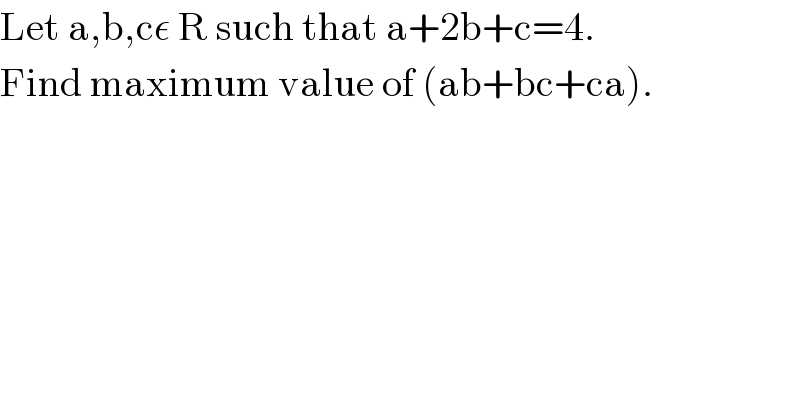
$$\mathrm{Let}\:\mathrm{a},\mathrm{b},\mathrm{c}\epsilon\:\mathrm{R}\:\mathrm{such}\:\mathrm{that}\:\mathrm{a}+\mathrm{2b}+\mathrm{c}=\mathrm{4}. \\ $$$$\mathrm{Find}\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{of}\:\left(\mathrm{ab}+\mathrm{bc}+\mathrm{ca}\right). \\ $$
Answered by MrW3 last updated on 18/Aug/18
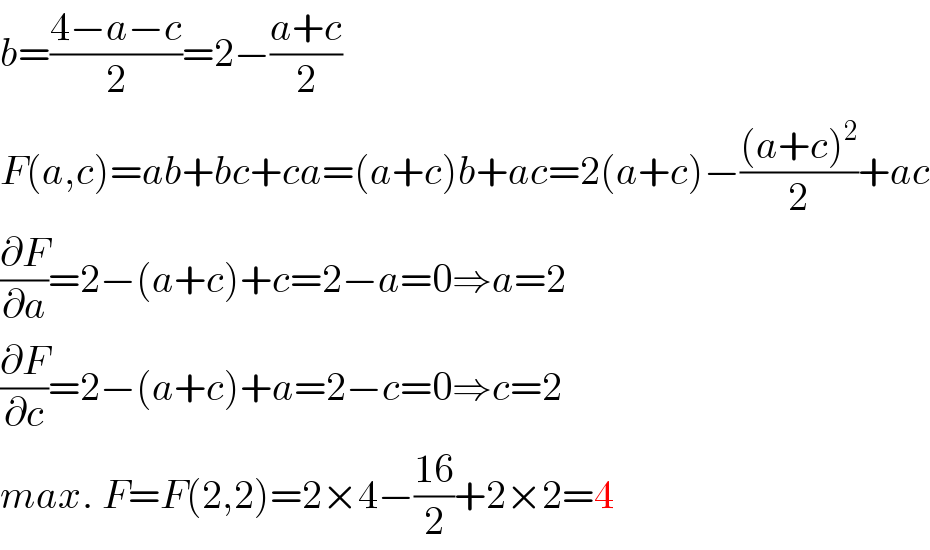
$${b}=\frac{\mathrm{4}−{a}−{c}}{\mathrm{2}}=\mathrm{2}−\frac{{a}+{c}}{\mathrm{2}} \\ $$$${F}\left({a},{c}\right)={ab}+{bc}+{ca}=\left({a}+{c}\right){b}+{ac}=\mathrm{2}\left({a}+{c}\right)−\frac{\left({a}+{c}\right)^{\mathrm{2}} }{\mathrm{2}}+{ac} \\ $$$$\frac{\partial{F}}{\partial{a}}=\mathrm{2}−\left({a}+{c}\right)+{c}=\mathrm{2}−{a}=\mathrm{0}\Rightarrow{a}=\mathrm{2} \\ $$$$\frac{\partial{F}}{\partial{c}}=\mathrm{2}−\left({a}+{c}\right)+{a}=\mathrm{2}−{c}=\mathrm{0}\Rightarrow{c}=\mathrm{2} \\ $$$${max}.\:{F}={F}\left(\mathrm{2},\mathrm{2}\right)=\mathrm{2}×\mathrm{4}−\frac{\mathrm{16}}{\mathrm{2}}+\mathrm{2}×\mathrm{2}=\mathrm{4} \\ $$
Commented by rahul 19 last updated on 18/Aug/18
Ausgezeichnet! ����
Commented by MrW3 last updated on 18/Aug/18
Danke sehr!
