Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 144603 by loveineq last updated on 26/Jun/21

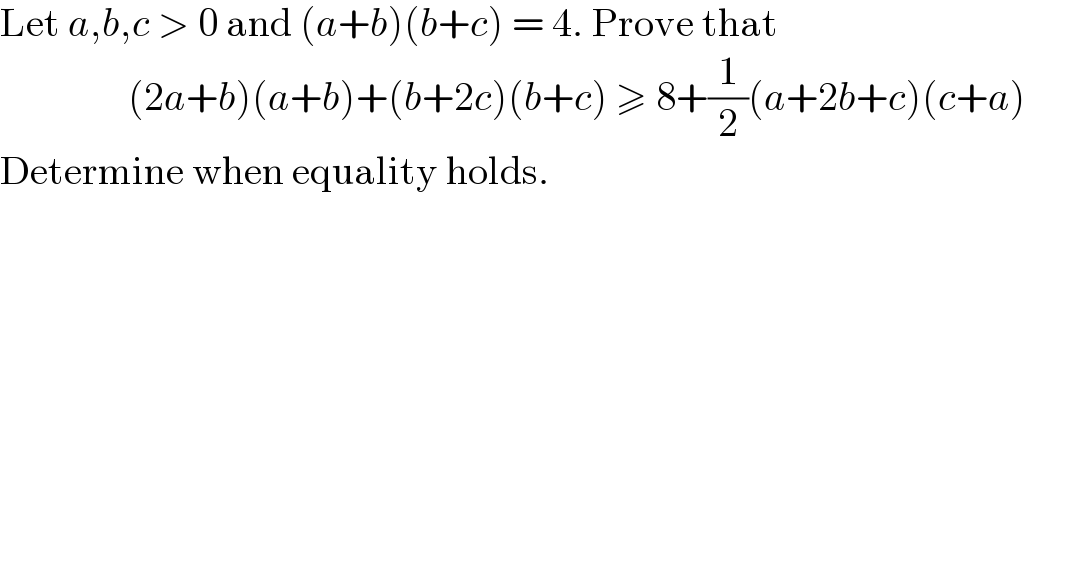
Let a,b,c > 0 and (a+b)(b+c) = 4. Prove that (2a+b)(a+b)+(b+2c)(b+c) ≥ 8+(1/2)(a+2b+c)(c+a) Determine when equality holds.

$$\mathrm{Let}\:{a},{b},{c}\:>\:\mathrm{0}\:\mathrm{and}\:\left({a}+{b}\right)\left({b}+{c}\right)\:=\:\mathrm{4}.\:\mathrm{Prove}\:\mathrm{that} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}{a}+{b}\right)\left({a}+{b}\right)+\left({b}+\mathrm{2}{c}\right)\left({b}+{c}\right)\:\geqslant\:\mathrm{8}+\frac{\mathrm{1}}{\mathrm{2}}\left({a}+\mathrm{2}{b}+{c}\right)\left({c}+{a}\right)\:\:\:\:\:\:\: \\ $$ $$\mathrm{Determine}\:\mathrm{when}\:\mathrm{equality}\:\mathrm{holds}.\:\:\: \\ $$

Answered by mindispower last updated on 27/Jun/21

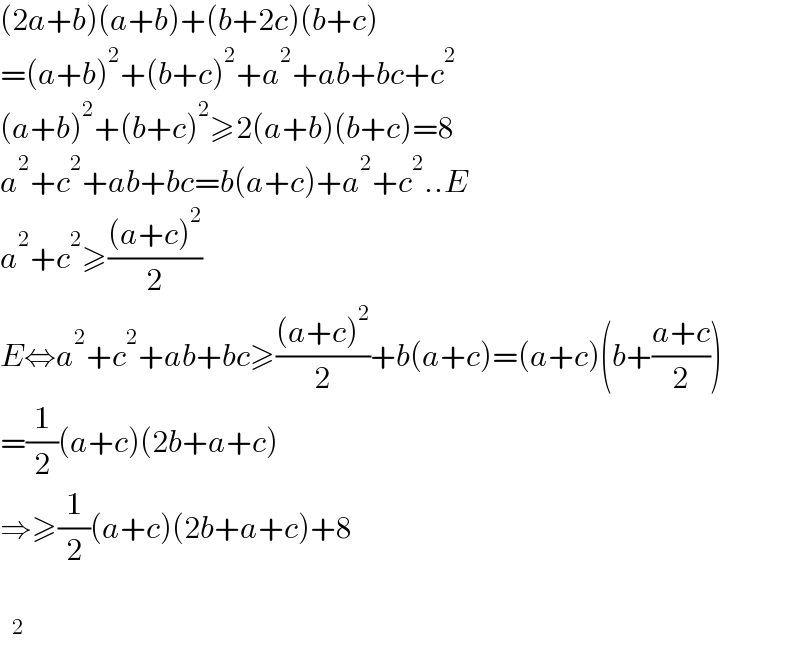
(2a+b)(a+b)+(b+2c)(b+c) =(a+b)^2 +(b+c)^2 +a^2 +ab+bc+c^2 (a+b)^2 +(b+c)^2 ≥2(a+b)(b+c)=8 a^2 +c^2 +ab+bc=b(a+c)+a^2 +c^2 ..E a^2 +c^2 ≥(((a+c)^2 )/2) E⇔a^2 +c^2 +ab+bc≥(((a+c)^2 )/2)+b(a+c)=(a+c)(b+((a+c)/2)) =(1/2)(a+c)(2b+a+c) ⇒≥(1/2)(a+c)(2b+a+c)+8

$$\left(\mathrm{2}{a}+{b}\right)\left({a}+{b}\right)+\left({b}+\mathrm{2}{c}\right)\left({b}+{c}\right) \\ $$ $$=\left({a}+{b}\right)^{\mathrm{2}} +\left({b}+{c}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} +{ab}+{bc}+{c}^{\mathrm{2}} \\ $$ $$\left({a}+{b}\right)^{\mathrm{2}} +\left({b}+{c}\right)^{\mathrm{2}} \geqslant\mathrm{2}\left({a}+{b}\right)\left({b}+{c}\right)=\mathrm{8} \\ $$ $${a}^{\mathrm{2}} +{c}^{\mathrm{2}} +{ab}+{bc}={b}\left({a}+{c}\right)+{a}^{\mathrm{2}} +{c}^{\mathrm{2}} ..{E} \\ $$ $${a}^{\mathrm{2}} +{c}^{\mathrm{2}} \geqslant\frac{\left({a}+{c}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$ $${E}\Leftrightarrow{a}^{\mathrm{2}} +{c}^{\mathrm{2}} +{ab}+{bc}\geqslant\frac{\left({a}+{c}\right)^{\mathrm{2}} }{\mathrm{2}}+{b}\left({a}+{c}\right)=\left({a}+{c}\right)\left({b}+\frac{{a}+{c}}{\mathrm{2}}\right) \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{c}\right)\left(\mathrm{2}{b}+{a}+{c}\right) \\ $$ $$\Rightarrow\geqslant\frac{\mathrm{1}}{\mathrm{2}}\left({a}+{c}\right)\left(\mathrm{2}{b}+{a}+{c}\right)+\mathrm{8} \\ $$ $$ \\ $$ $$ \\ $$

Commented byloveineq last updated on 27/Jun/21

thanks

$${thanks} \\ $$

Commented bymindispower last updated on 27/Jun/21

pleasur

$${pleasur} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com